FairBED: A Bayesian Experimental Design Approach to Gathering Fairer Data

Frameworks for ensuring fairness in machine learning typically focus on learning fair models from existing data. But this endeavor is often undermined by biases already present in that data. We therefore look to modify the data acquisition process itself to help gather fairer data that is inherently more suitable for training fair predictors. To this end, we introduce FairBED, which provides novel formulations for quantifying the fairness of datasets themselves based on the idea that fair datasets should be uninformative about sensitive attributes. We then use this to construct practical fairness-aware Bayesian experimental design (BED) objectives that maximize expected information gain about the target quantity of interest while minimizing expected information gain about sensitive attributes. We further derive a theoretical link between FairBED and demographic parity, and show empirically that models trained on data gathered using FairBED provide improved fairness-accuracy trade-offs compared to randomly acquired data and conventional BED.

Learning from data with structured missingness

Missing data are an unavoidable complication in many machine learning tasks. When data are `missing at random' there exist a range of tools and techniques to deal with the issue. However, as machine learning studies become more ambitious, and seek to learn from ever-larger volumes of heterogeneous data, an increasingly encountered problem arises in which missing values exhibit an association or structure, either explicitly or implicitly. Such `structured missingness' raises a range of challenges that have not yet been systematically addressed, and presents a fundamental hindrance to machine learning at scale. Here, we outline the current literature and propose a set of grand challenges in learning from data with structured missingness.

Density Estimation with Autoregressive Bayesian Predictives

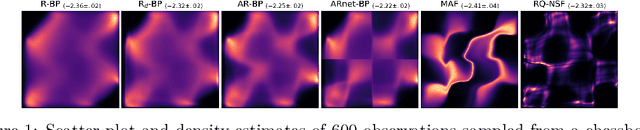
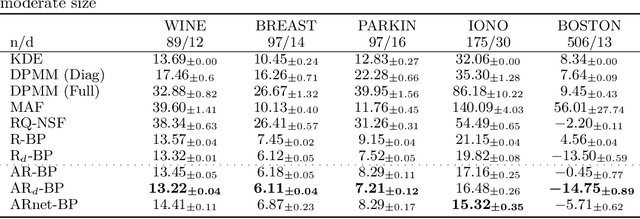
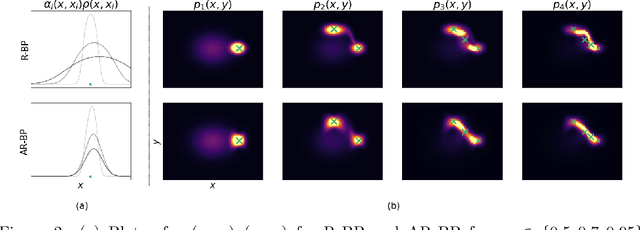
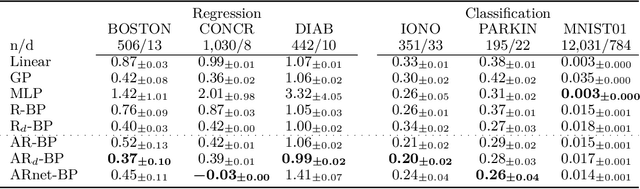
Bayesian methods are a popular choice for statistical inference in small-data regimes due to the regularization effect induced by the prior, which serves to counteract overfitting. In the context of density estimation, the standard Bayesian approach is to target the posterior predictive. In general, direct estimation of the posterior predictive is intractable and so methods typically resort to approximating the posterior distribution as an intermediate step. The recent development of recursive predictive copula updates, however, has made it possible to perform tractable predictive density estimation without the need for posterior approximation. Although these estimators are computationally appealing, they tend to struggle on non-smooth data distributions. This is largely due to the comparatively restrictive form of the likelihood models from which the proposed copula updates were derived. To address this shortcoming, we consider a Bayesian nonparametric model with an autoregressive likelihood decomposition and Gaussian process prior, which yields a data-dependent bandwidth parameter in the copula update. Further, we formulate a novel parameterization of the bandwidth using an autoregressive neural network that maps the data into a latent space, and is thus able to capture more complex dependencies in the data. Our extensions increase the modelling capacity of existing recursive Bayesian density estimators, achieving state-of-the-art results on tabular data sets.

Neural Score Matching for High-Dimensional Causal Inference

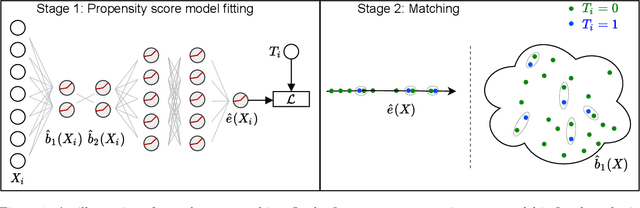
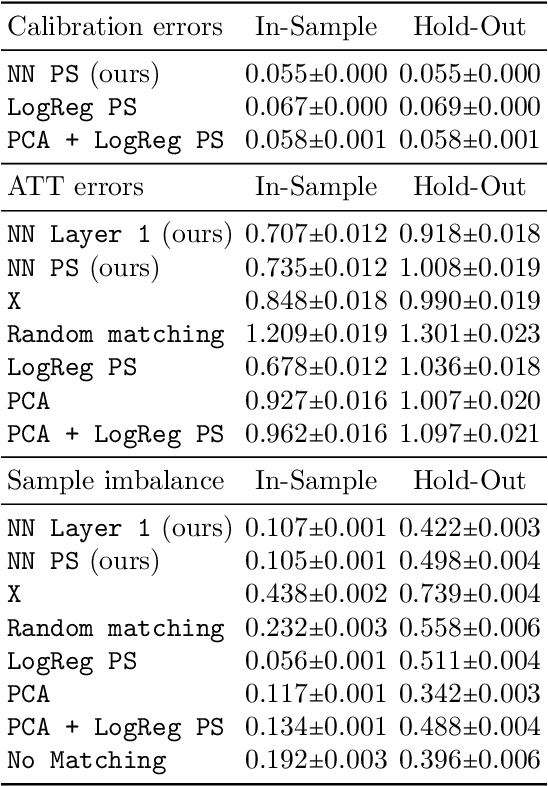
Traditional methods for matching in causal inference are impractical for high-dimensional datasets. They suffer from the curse of dimensionality: exact matching and coarsened exact matching find exponentially fewer matches as the input dimension grows, and propensity score matching may match highly unrelated units together. To overcome this problem, we develop theoretical results which motivate the use of neural networks to obtain non-trivial, multivariate balancing scores of a chosen level of coarseness, in contrast to the classical, scalar propensity score. We leverage these balancing scores to perform matching for high-dimensional causal inference and call this procedure neural score matching. We show that our method is competitive against other matching approaches on semi-synthetic high-dimensional datasets, both in terms of treatment effect estimation and reducing imbalance.