Learning from data with structured missingness

Missing data are an unavoidable complication in many machine learning tasks. When data are `missing at random' there exist a range of tools and techniques to deal with the issue. However, as machine learning studies become more ambitious, and seek to learn from ever-larger volumes of heterogeneous data, an increasingly encountered problem arises in which missing values exhibit an association or structure, either explicitly or implicitly. Such `structured missingness' raises a range of challenges that have not yet been systematically addressed, and presents a fundamental hindrance to machine learning at scale. Here, we outline the current literature and propose a set of grand challenges in learning from data with structured missingness.

Where the Bee Sucks -- A Dynamic Bayesian Network Approach to Decision Support for Pollinator Abundance Strategies

For policymakers wishing to make evidence-based decisions, one of the challenges is how to combine the relevant information and evidence in a coherent and defensible manner in order to formulate and evaluate candidate policies. Policymakers often need to rely on experts with disparate fields of expertise when making policy choices in complex, multi-faceted, dynamic environments such as those dealing with ecosystem services. The pressures affecting the survival and pollination capabilities of honey bees (Apis mellifera), wild bees and other pollinators is well-documented, but incomplete. In order to estimate the potential effectiveness of various candidate policies to support pollination services, there is an urgent need to quantify the effect of various combinations of variables on the pollination ecosystem service, utilising available information, models and expert judgement. In this paper, we present a new application of the integrating decision support system methodology for combining inputs from multiple panels of experts to evaluate policies to support an abundant pollinator population.

cegpy: Modelling with Chain Event Graphs in Python

Chain event graphs (CEGs) are a recent family of probabilistic graphical models that generalise the popular Bayesian networks (BNs) family. Crucially, unlike BNs, a CEG is able to embed, within its graph and its statistical model, asymmetries exhibited by a process. These asymmetries might be in the conditional independence relationships or in the structure of the graph and its underlying event space. Structural asymmetries are common in many domains, and can occur naturally (e.g. a defendant vs prosecutor's version of events) or by design (e.g. a public health intervention). However, there currently exists no software that allows a user to leverage the theoretical developments of the CEG model family in modelling processes with structural asymmetries. This paper introduces cegpy, the first Python package for learning and analysing complex processes using CEGs. The key feature of cegpy is that it is the first CEG package in any programming language that can model processes with symmetric as well as asymmetric structures. cegpy contains an implementation of Bayesian model selection and probability propagation algorithms for CEGs. We illustrate the functionality of cegpy using a structurally asymmetric dataset.

Beyond Conjugacy for Chain Event Graph Model Selection

Chain event graphs are a family of probabilistic graphical models that generalise Bayesian networks and have been successfully applied to a wide range of domains. Unlike Bayesian networks, these models can encode context-specific conditional independencies as well as asymmetric developments within the evolution of a process. More recently, new model classes belonging to the chain event graph family have been developed for modelling time-to-event data to study the temporal dynamics of a process. However, existing model selection algorithms for chain event graphs and its variants rely on all parameters having conjugate priors. This is unrealistic for many real-world applications. In this paper, we propose a mixture modelling approach to model selection in chain event graphs that does not rely on conjugacy. Moreover, we also show that this methodology is more amenable to being robustly scaled than the existing model selection algorithms used for this family. We demonstrate our techniques on simulated datasets.

Propagation for Dynamic Continuous Time Chain Event Graphs

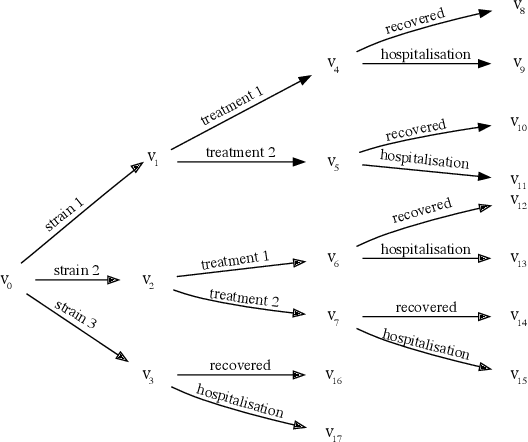
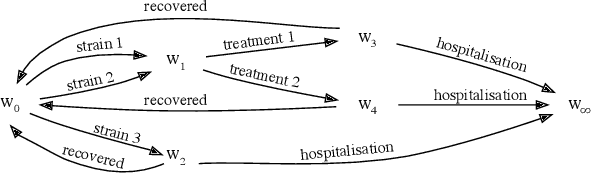
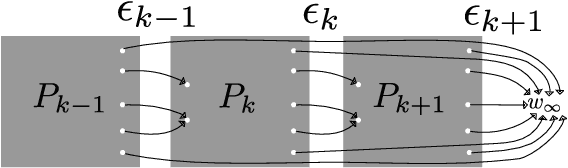
Chain Event Graphs (CEGs) are a family of event-based graphical models that represent context-specific conditional independences typically exhibited by asymmetric state space problems. The class of continuous time dynamic CEGs (CT-DCEGs) provides a factored representation of longitudinally evolving trajectories of a process in continuous time. Temporal evidence in a CT-DCEG introduces dependence between its transition and holding time distributions. We present a tractable exact inferential scheme analogous to the scheme in Kj{\ae}rulff (1992) for discrete Dynamic Bayesian Networks (DBNs) which employs standard junction tree inference by "unrolling" the DBN. To enable this scheme, we present an extension of the standard CEG propagation algorithm (Thwaites et al., 2008). Interestingly, the CT-DCEG benefits from simplification of its graph on observing compatible evidence while preserving the still relevant symmetries within the asymmetric network. Our results indicate that the CT-DCEG is preferred to DBNs and continuous time BNs under contexts involving significant asymmetry and a natural total ordering of the process evolution.

Constructing a Chain Event Graph from a Staged Tree

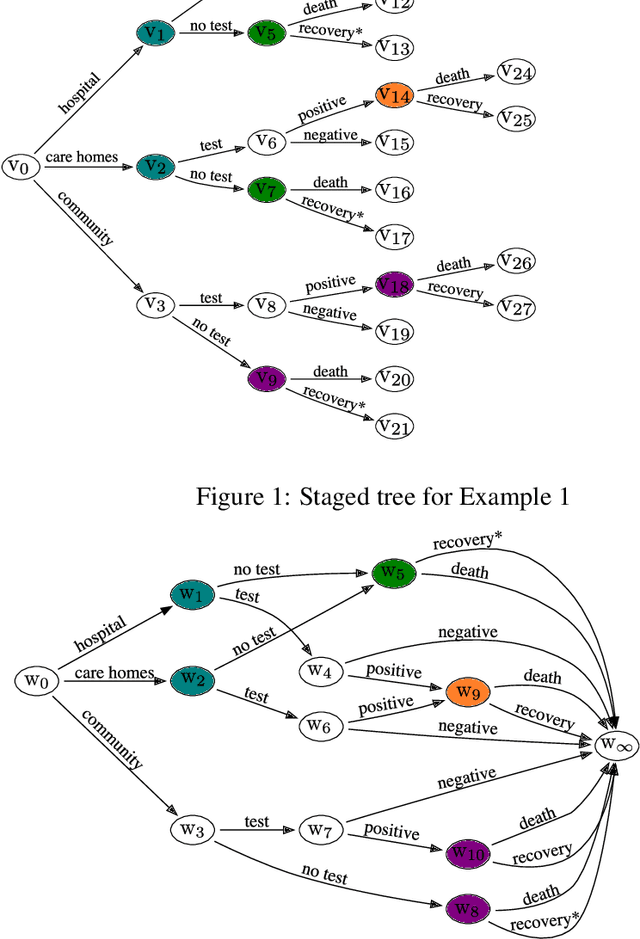
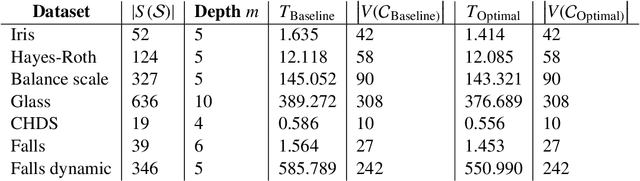
Chain Event Graphs (CEGs) are a recent family of probabilistic graphical models - a generalisation of Bayesian Networks - providing an explicit representation of structural zeros and context-specific conditional independences within their graph topology. A CEG is constructed from an event tree through a sequence of transformations beginning with the colouring of the vertices of the event tree to identify one-step transition symmetries. This coloured event tree, also known as a staged tree, is the output of the learning algorithms used for this family. Surprisingly, no general algorithm has yet been devised that automatically transforms any staged tree into a CEG representation. In this paper we provide a simple iterative backward algorithm for this transformation. Additionally, we show that no information is lost from transforming a staged tree into a CEG. Finally, we demonstrate that with an optimal stopping time, our algorithm is more efficient than the generalisation of a special case presented in Silander and Leong (2013). We also provide Python code using this algorithm to obtain a CEG from any staged tree along with the functionality to add edges with sampling zeros.