The diameter of a stochastic matrix: A new measure for sensitivity analysis in Bayesian networks

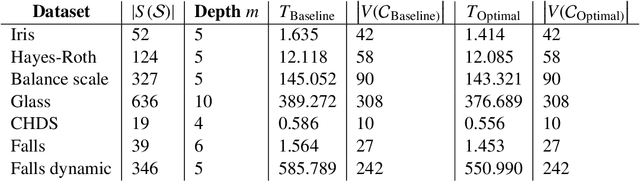
Bayesian networks are one of the most widely used classes of probabilistic models for risk management and decision support because of their interpretability and flexibility in including heterogeneous pieces of information. In any applied modelling, it is critical to assess how robust the inferences on certain target variables are to changes in the model. In Bayesian networks, these analyses fall under the umbrella of sensitivity analysis, which is most commonly carried out by quantifying dissimilarities using Kullback-Leibler information measures. In this paper, we argue that robustness methods based instead on the familiar total variation distance provide simple and more valuable bounds on robustness to misspecification, which are both formally justifiable and transparent. We introduce a novel measure of dependence in conditional probability tables called the diameter to derive such bounds. This measure quantifies the strength of dependence between a variable and its parents. We demonstrate how such formal robustness considerations can be embedded in building a Bayesian network.

Lexical semantic change for Ancient Greek and Latin

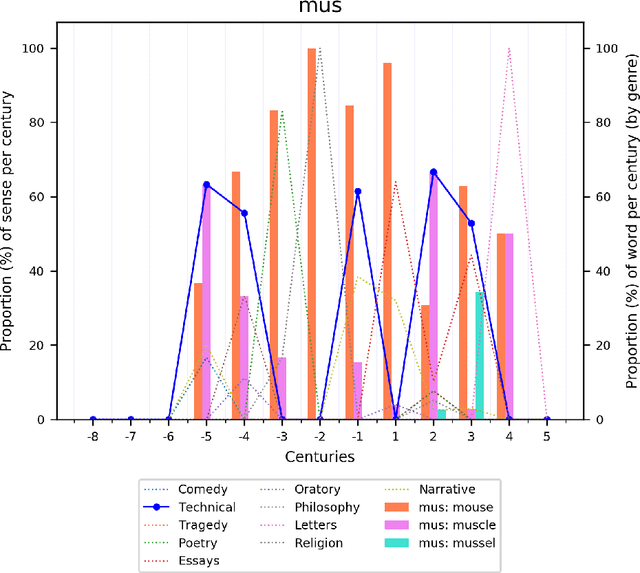
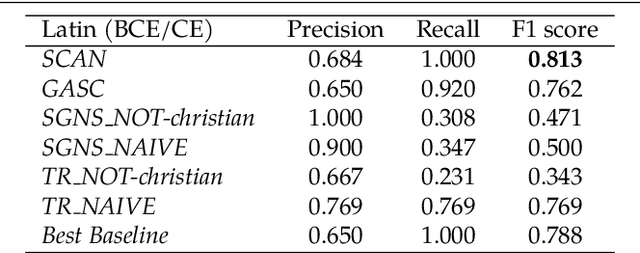
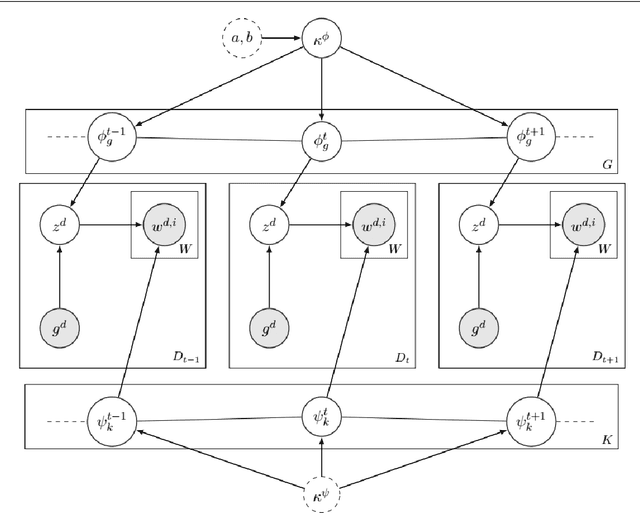
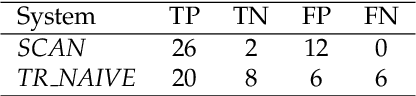
Change and its precondition, variation, are inherent in languages. Over time, new words enter the lexicon, others become obsolete, and existing words acquire new senses. Associating a word's correct meaning in its historical context is a central challenge in diachronic research. Historical corpora of classical languages, such as Ancient Greek and Latin, typically come with rich metadata, and existing models are limited by their inability to exploit contextual information beyond the document timestamp. While embedding-based methods feature among the current state of the art systems, they are lacking in the interpretative power. In contrast, Bayesian models provide explicit and interpretable representations of semantic change phenomena. In this chapter we build on GASC, a recent computational approach to semantic change based on a dynamic Bayesian mixture model. In this model, the evolution of word senses over time is based not only on distributional information of lexical nature, but also on text genres. We provide a systematic comparison of dynamic Bayesian mixture models for semantic change with state-of-the-art embedding-based models. On top of providing a full description of meaning change over time, we show that Bayesian mixture models are highly competitive approaches to detect binary semantic change in both Ancient Greek and Latin.

Propagation for Dynamic Continuous Time Chain Event Graphs

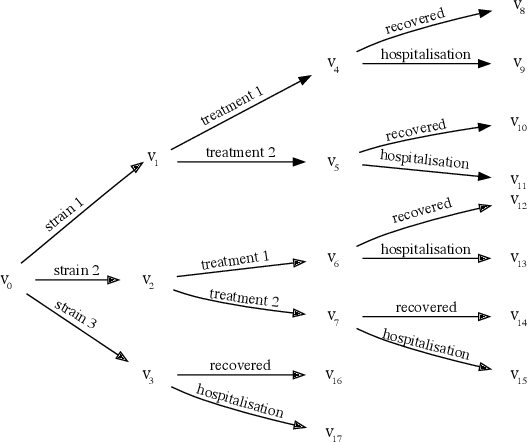
Chain Event Graphs (CEGs) are a family of event-based graphical models that represent context-specific conditional independences typically exhibited by asymmetric state space problems. The class of continuous time dynamic CEGs (CT-DCEGs) provides a factored representation of longitudinally evolving trajectories of a process in continuous time. Temporal evidence in a CT-DCEG introduces dependence between its transition and holding time distributions. We present a tractable exact inferential scheme analogous to the scheme in Kj{\ae}rulff (1992) for discrete Dynamic Bayesian Networks (DBNs) which employs standard junction tree inference by "unrolling" the DBN. To enable this scheme, we present an extension of the standard CEG propagation algorithm (Thwaites et al., 2008). Interestingly, the CT-DCEG benefits from simplification of its graph on observing compatible evidence while preserving the still relevant symmetries within the asymmetric network. Our results indicate that the CT-DCEG is preferred to DBNs and continuous time BNs under contexts involving significant asymmetry and a natural total ordering of the process evolution.

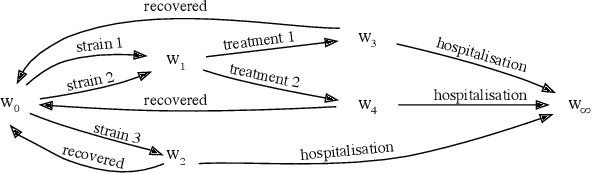
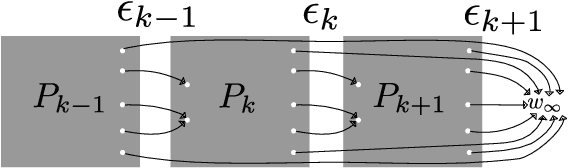
Constructing a Chain Event Graph from a Staged Tree

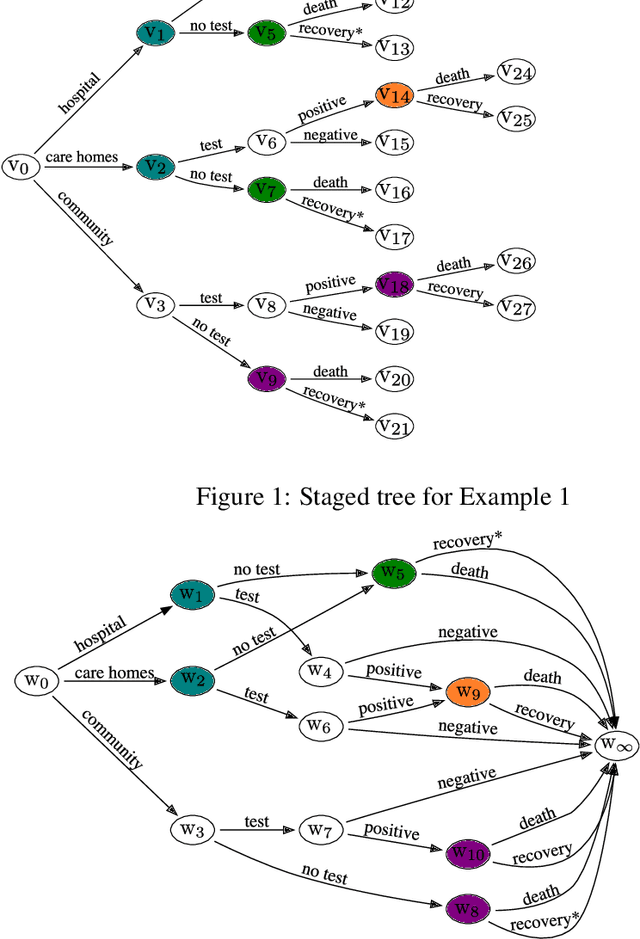
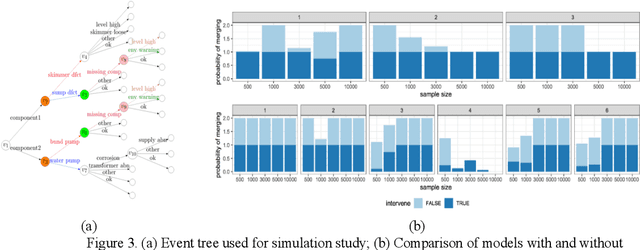
Chain Event Graphs (CEGs) are a recent family of probabilistic graphical models - a generalisation of Bayesian Networks - providing an explicit representation of structural zeros and context-specific conditional independences within their graph topology. A CEG is constructed from an event tree through a sequence of transformations beginning with the colouring of the vertices of the event tree to identify one-step transition symmetries. This coloured event tree, also known as a staged tree, is the output of the learning algorithms used for this family. Surprisingly, no general algorithm has yet been devised that automatically transforms any staged tree into a CEG representation. In this paper we provide a simple iterative backward algorithm for this transformation. Additionally, we show that no information is lost from transforming a staged tree into a CEG. Finally, we demonstrate that with an optimal stopping time, our algorithm is more efficient than the generalisation of a special case presented in Silander and Leong (2013). We also provide Python code using this algorithm to obtain a CEG from any staged tree along with the functionality to add edges with sampling zeros.

Bayesian Learning of Causal Relationships for System Reliability

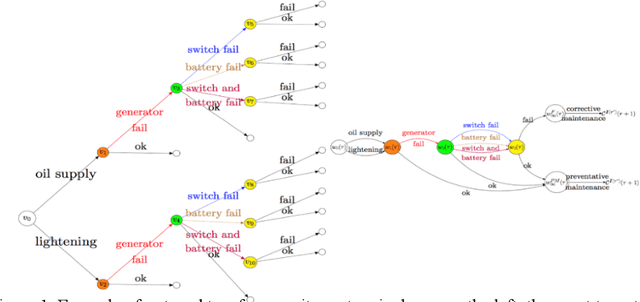
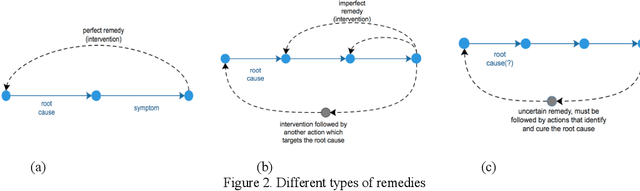
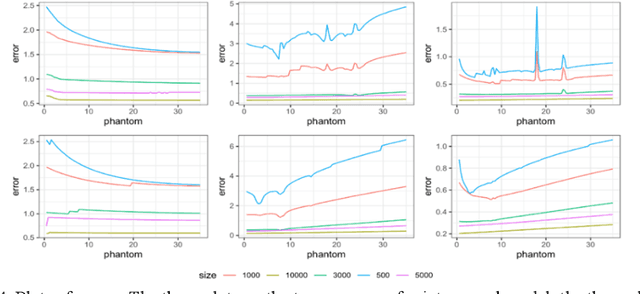
Causal theory is now widely developed with many applications to medicine and public health. However within the discipline of reliability, although causation is a key concept in this field, there has been much less theoretical attention. In this paper, we will demonstrate how some aspects of established causal methodology can be translated via trees, and more specifically chain event graphs, into domain of reliability theory to help the probability modeling of failures. We further show how various domain specific concepts of causality particular to reliability can be imported into more generic causal algebras and so demonstrate how these disciplines can inform each other. This paper is informed by a detailed analysis of maintenance records associated with a large electrical distribution company. Causal hypotheses embedded within these natural language texts are extracted and analyzed using the new graphical framework we introduced here.

GASC: Genre-Aware Semantic Change for Ancient Greek

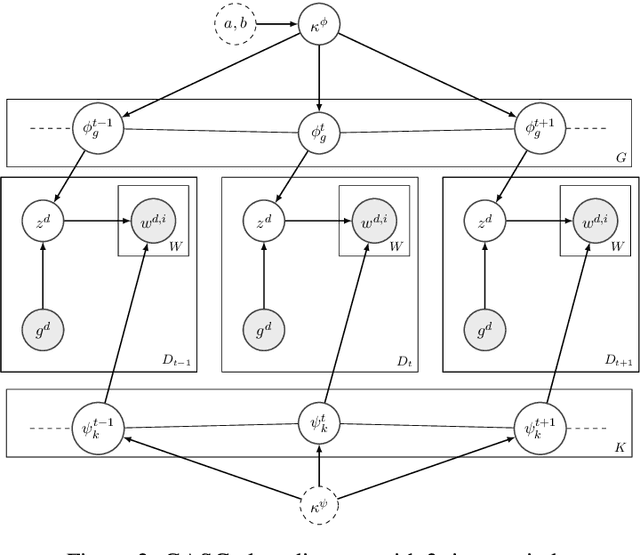
Word meaning changes over time, depending on linguistic and extra-linguistic factors. Associating a word's correct meaning in its historical context is a critical challenge in diachronic research, and is relevant to a range of NLP tasks, including information retrieval and semantic search in historical texts. Bayesian models for semantic change have emerged as a powerful tool to address this challenge, providing explicit and interpretable representations of semantic change phenomena. However, while corpora typically come with rich metadata, existing models are limited by their inability to exploit contextual information (such as text genre) beyond the document time-stamp. This is particularly critical in the case of ancient languages, where lack of data and long diachronic span make it harder to draw a clear distinction between polysemy and semantic change, and current systems perform poorly on these languages. We develop GASC, a dynamic semantic change model that leverages categorical metadata about the texts' genre information to boost inference and uncover the evolution of meanings in Ancient Greek corpora. In a new evaluation framework, we show that our model achieves improved predictive performance compared to the state of the art.

Properties of an N Time-Slice Dynamic Chain Event Graph

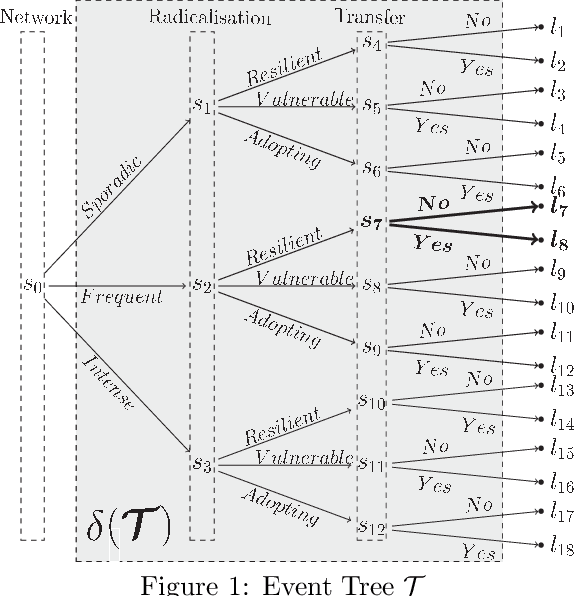
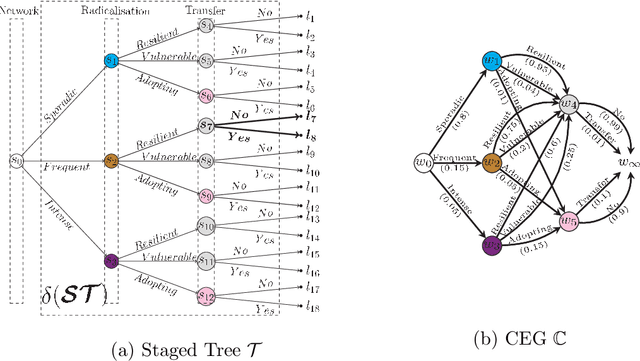
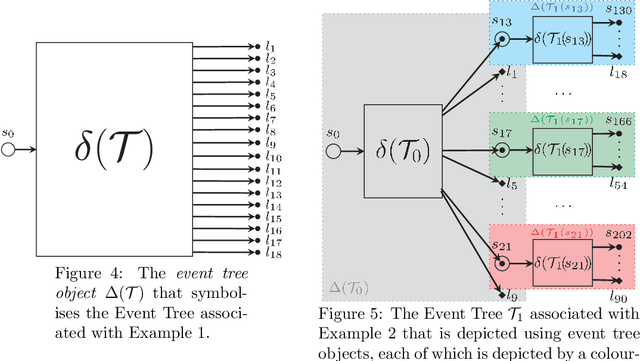
A Dynamic Chain Event Graph (DCEG) provides a rich tree-based framework for modelling a dynamic process with highly asymmetric developments. An N Time-Slice DCEG (NT-DCEG) is a useful subclass of the DCEG class that exhibits a specific type of periodicity in its supporting tree graph and embodies a time-homogeneity assumption. Here some desired properties of an NT-DCEG is explored. In particular, we prove that the class of NT-DCEGs contains all discrete N time-slice Dynamic Bayesian Networks as special cases. We also develop a method to distributively construct an NT-DCEG model. By exploiting the topology of an NT-DCEG graph, we show how to construct intrinsic random variables which exhibit context-specific independences that can then be checked by domain experts. We also show how an NT-DCEG can be used to depict various structural and Granger causal hypotheses about a given process. Our methods are illustrated throughout using examples of dynamic multivariate processes describing inmate radicalisation in a prison.

An N Time-Slice Dynamic Chain Event Graph

The Dynamic Chain Event Graph (DCEG) is able to depict many classes of discrete random processes exhibiting asymmetries in their developments and context-specific conditional probabilities structures. However, paradoxically, this very generality has so far frustrated its wide application. So in this paper we develop an object-oriented method to fully analyse a particularly useful and feasibly implementable new subclass of these graphical models called the N Time-Slice DCEG (NT-DCEG). After demonstrating a close relationship between an NT-DCEG and a specific class of Markov processes, we discuss how graphical modellers can exploit this connection to gain a deep understanding of their processes. We also show how to read from the topology of this graph context-specific independence statements that can then be checked by domain experts. Our methods are illustrated throughout using examples of dynamic multivariate processes describing inmate radicalisation in a prison.

A symbolic algebra for the computation of expected utilities in multiplicative influence diagrams

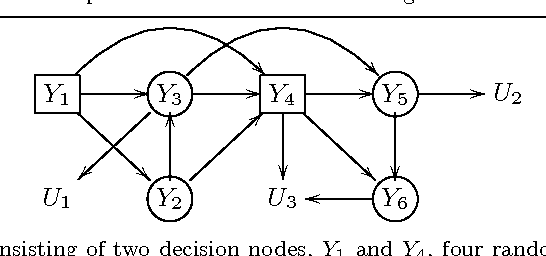
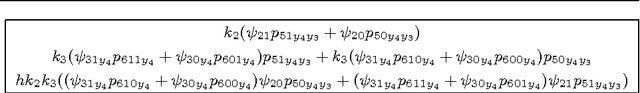
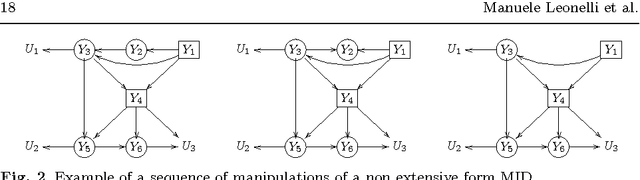
Influence diagrams provide a compact graphical representation of decision problems. Several algorithms for the quick computation of their associated expected utilities are available in the literature. However, often they rely on a full quantification of both probabilistic uncertainties and utility values. For problems where all random variables and decision spaces are finite and discrete, here we develop a symbolic way to calculate the expected utilities of influence diagrams that does not require a full numerical representation. Within this approach expected utilities correspond to families of polynomials. After characterizing their polynomial structure, we develop an efficient symbolic algorithm for the propagation of expected utilities through the diagram and provide an implementation of this algorithm using a computer algebra system. We then characterize many of the standard manipulations of influence diagrams as transformations of polynomials. We also generalize the decision analytic framework of these diagrams by defining asymmetries as operations over the expected utility polynomials.

Directed expected utility networks

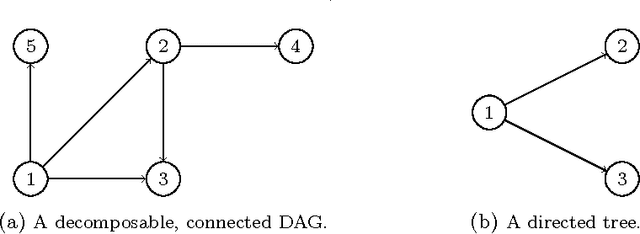
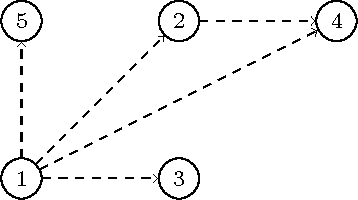
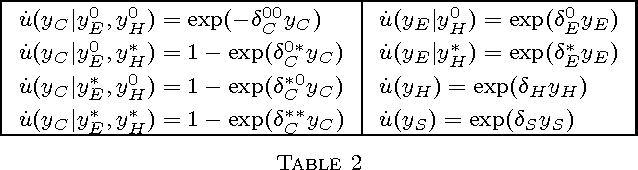
A variety of statistical graphical models have been defined to represent the conditional independences underlying a random vector of interest. Similarly, many different graphs embedding various types of preferential independences, as for example conditional utility independence and generalized additive independence, have more recently started to appear. In this paper we define a new graphical model, called a directed expected utility network, whose edges depict both probabilistic and utility conditional independences. These embed a very flexible class of utility models, much larger than those usually conceived in standard influence diagrams. Our graphical representation, and various transformations of the original graph into a tree structure, are then used to guide fast routines for the computation of a decision problem's expected utilities. We show that our routines generalize those usually utilized in standard influence diagrams' evaluations under much more restrictive conditions. We then proceed with the construction of a directed expected utility network to support decision makers in the domain of household food security.