Rodrigo A. Collazo
Properties of an N Time-Slice Dynamic Chain Event Graph
Oct 22, 2018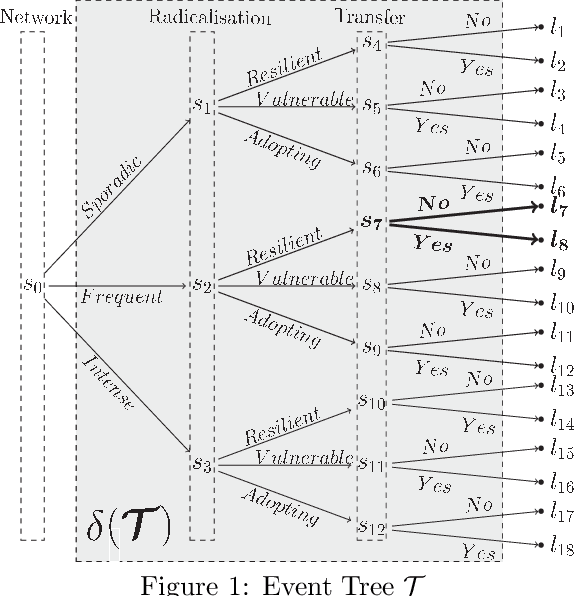
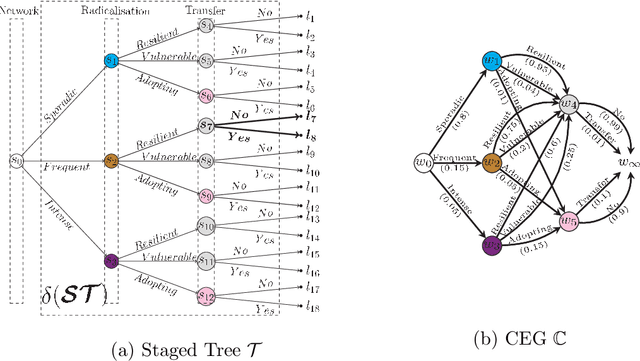
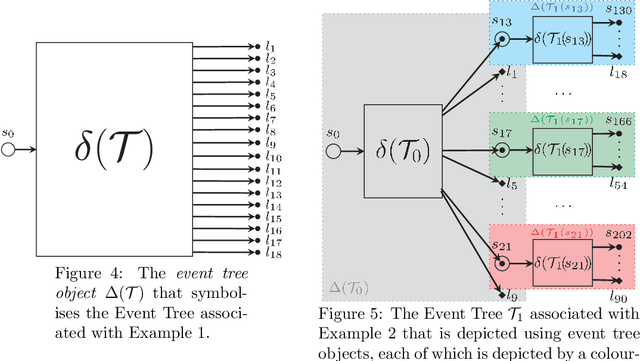
Abstract:A Dynamic Chain Event Graph (DCEG) provides a rich tree-based framework for modelling a dynamic process with highly asymmetric developments. An N Time-Slice DCEG (NT-DCEG) is a useful subclass of the DCEG class that exhibits a specific type of periodicity in its supporting tree graph and embodies a time-homogeneity assumption. Here some desired properties of an NT-DCEG is explored. In particular, we prove that the class of NT-DCEGs contains all discrete N time-slice Dynamic Bayesian Networks as special cases. We also develop a method to distributively construct an NT-DCEG model. By exploiting the topology of an NT-DCEG graph, we show how to construct intrinsic random variables which exhibit context-specific independences that can then be checked by domain experts. We also show how an NT-DCEG can be used to depict various structural and Granger causal hypotheses about a given process. Our methods are illustrated throughout using examples of dynamic multivariate processes describing inmate radicalisation in a prison.
An N Time-Slice Dynamic Chain Event Graph
Aug 17, 2018


Abstract:The Dynamic Chain Event Graph (DCEG) is able to depict many classes of discrete random processes exhibiting asymmetries in their developments and context-specific conditional probabilities structures. However, paradoxically, this very generality has so far frustrated its wide application. So in this paper we develop an object-oriented method to fully analyse a particularly useful and feasibly implementable new subclass of these graphical models called the N Time-Slice DCEG (NT-DCEG). After demonstrating a close relationship between an NT-DCEG and a specific class of Markov processes, we discuss how graphical modellers can exploit this connection to gain a deep understanding of their processes. We also show how to read from the topology of this graph context-specific independence statements that can then be checked by domain experts. Our methods are illustrated throughout using examples of dynamic multivariate processes describing inmate radicalisation in a prison.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge