Estimating Staged Event Tree Models via Hierarchical Clustering on the Simplex

Staged tree models enhance Bayesian networks by incorporating context-specific dependencies through a stage-based structure. In this study, we present a new framework for estimating staged trees using hierarchical clustering on the probability simplex, utilizing simplex basesd divergences. We conduct a thorough evaluation of several distance and divergence metrics including Total Variation, Hellinger, Fisher, and Kaniadakis; alongside various linkage methods such as Ward.D2, average, complete, and McQuitty. We conducted the simulation experiments that reveals Total Variation, especially when combined with Ward.D2 linkage, consistently produces staged trees with better model fit, structure recovery, and computational efficiency. We assess performance by utilizing relative Bayesian Information Criterion (BIC), and Hamming distance. Our findings indicate that although Backward Hill Climbing (BHC) delivers competitive outcomes, it incurs a significantly higher computational cost. On the other, Total Variation divergence with Ward.D2 linkage, achieves similar performance while providing significantly better computational efficiency, making it a more viable option for large-scale or time sensitive tasks.

Learning Staged Trees from Incomplete Data

Staged trees are probabilistic graphical models capable of representing any class of non-symmetric independence via a coloring of its vertices. Several structural learning routines have been defined and implemented to learn staged trees from data, under the frequentist or Bayesian paradigm. They assume a data set has been observed fully and, in practice, observations with missing entries are either dropped or imputed before learning the model. Here, we introduce the first algorithms for staged trees that handle missingness within the learning of the model. To this end, we characterize the likelihood of staged tree models in the presence of missing data and discuss pseudo-likelihoods that approximate it. A structural expectation-maximization algorithm estimating the model directly from the full likelihood is also implemented and evaluated. A computational experiment showcases the performance of the novel learning algorithms, demonstrating that it is feasible to account for different missingness patterns when learning staged trees.

The R Package stagedtrees for Structural Learning of Stratified Staged Trees

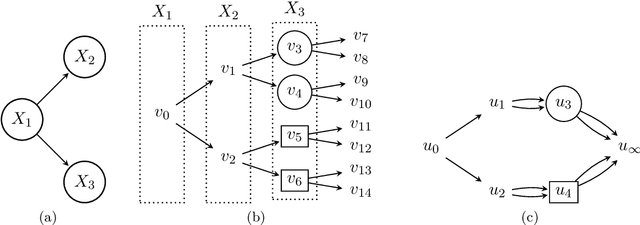
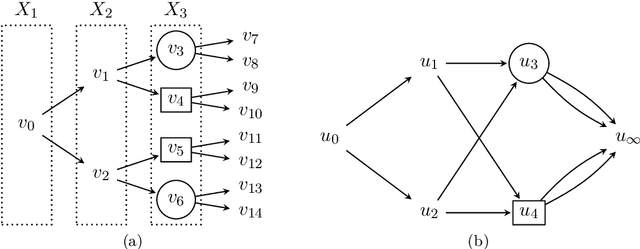
stagedtrees is an R package which includes several algorithms for learning the structure of staged trees and chain event graphs from data. Score-based and distance-based algorithms are implemented, as well as various functionalities to plot the models and perform inference. The capabilities of stagedtrees are illustrated using mainly two datasets both included in the package or bundled in R.

A geometric characterisation of sensitivity analysis in monomial models

Sensitivity analysis in probabilistic discrete graphical models is usually conducted by varying one probability value at a time and observing how this affects output probabilities of interest. When one probability is varied then others are proportionally covaried to respect the sum-to-one condition of probability laws. The choice of proportional covariation is justified by a variety of optimality conditions, under which the original and the varied distributions are as close as possible under different measures of closeness. For variations of more than one parameter at a time proportional covariation is justified in some special cases only. In this work, for the large class of discrete statistical models entertaining a regular monomial parametrisation, we demonstrate the optimality of newly defined proportional multi-way schemes with respect to an optimality criterion based on the notion of I-divergence. We demonstrate that there are varying parameters choices for which proportional covariation is not optimal and identify the sub-family of model distributions where the distance between the original distribution and the one where probabilities are covaried proportionally is minimum. This is shown by adopting a new formal, geometric characterization of sensitivity analysis in monomial models, which include a wide array of probabilistic graphical models. We also demonstrate the optimality of proportional covariation for multi-way analyses in Naive Bayes classifiers.

Markov Property in Generative Classifiers

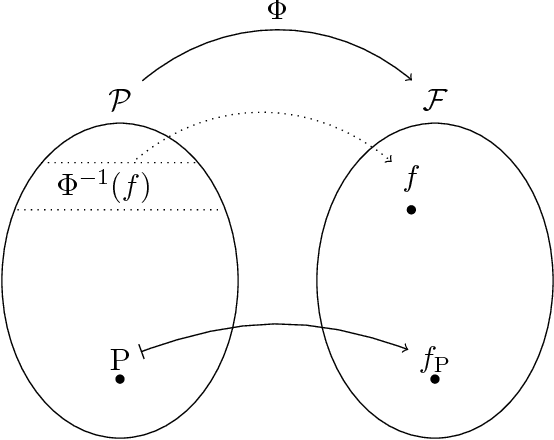
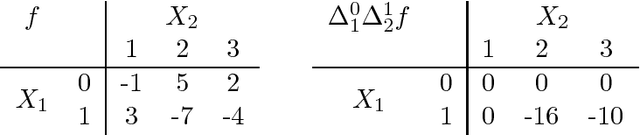
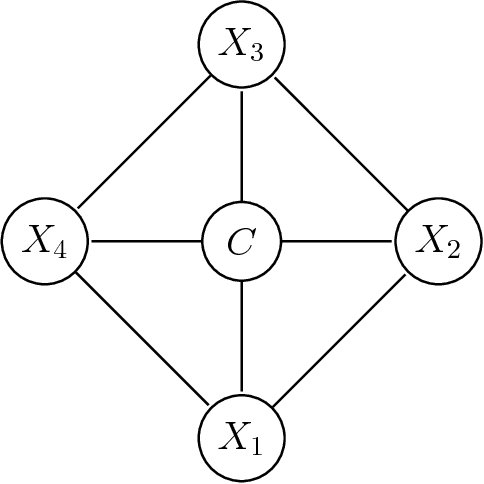
We show that, for generative classifiers, conditional independence corresponds to linear constraints for the induced discrimination functions. Discrimination functions of undirected Markov network classifiers can thus be characterized by sets of linear constraints. These constraints are represented by a second order finite difference operator over functions of categorical variables. As an application we study the expressive power of generative classifiers under the undirected Markov property and we present a general method to combine discriminative and generative classifiers.

A symbolic algebra for the computation of expected utilities in multiplicative influence diagrams

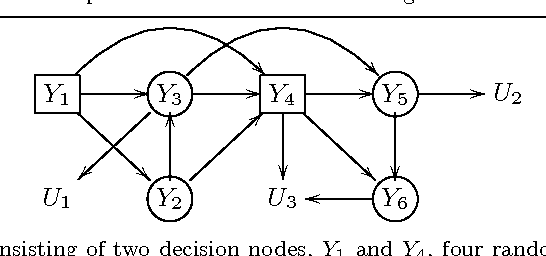
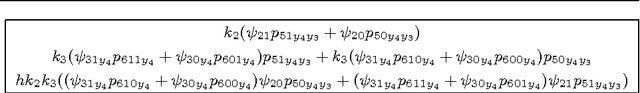
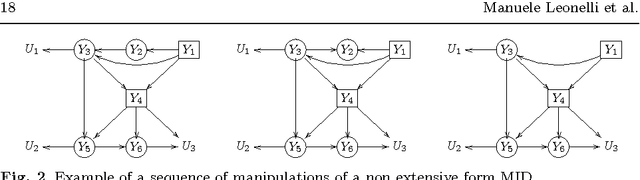
Influence diagrams provide a compact graphical representation of decision problems. Several algorithms for the quick computation of their associated expected utilities are available in the literature. However, often they rely on a full quantification of both probabilistic uncertainties and utility values. For problems where all random variables and decision spaces are finite and discrete, here we develop a symbolic way to calculate the expected utilities of influence diagrams that does not require a full numerical representation. Within this approach expected utilities correspond to families of polynomials. After characterizing their polynomial structure, we develop an efficient symbolic algorithm for the propagation of expected utilities through the diagram and provide an implementation of this algorithm using a computer algebra system. We then characterize many of the standard manipulations of influence diagrams as transformations of polynomials. We also generalize the decision analytic framework of these diagrams by defining asymmetries as operations over the expected utility polynomials.

Adaptive Experimental Design for Path-following Performance Assessment of Unmanned Vehicles

The definition of Good Experimental Methodologies (GEMs) in robotics is a topic of widespread interest due also to the increasing employment of robots in everyday civilian life. The present work contributes to the ongoing discussion on GEMs for Unmanned Surface Vehicles (USVs). It focuses on the definition of GEMs and provides specific guidelines for path-following experiments. Statistically designed experiments (DoE) offer a valid basis for developing an empirical model of the system being investigated. A two-step adaptive experimental procedure for evaluating path-following performance and based on DoE, is tested on the simulator of the Charlie USV. The paper argues the necessity of performing extensive simulations prior to the execution of field trials.