bnRep: A repository of Bayesian networks from the academic literature

Bayesian networks (BNs) are widely used for modeling complex systems with uncertainty, yet repositories of pre-built BNs remain limited. This paper introduces bnRep, an open-source R package offering a comprehensive collection of documented BNs, facilitating benchmarking, replicability, and education. With over 200 networks from academic publications, bnRep integrates seamlessly with bnlearn and other R packages, providing users with interactive tools for network exploration.

The diameter of a stochastic matrix: A new measure for sensitivity analysis in Bayesian networks

Bayesian networks are one of the most widely used classes of probabilistic models for risk management and decision support because of their interpretability and flexibility in including heterogeneous pieces of information. In any applied modelling, it is critical to assess how robust the inferences on certain target variables are to changes in the model. In Bayesian networks, these analyses fall under the umbrella of sensitivity analysis, which is most commonly carried out by quantifying dissimilarities using Kullback-Leibler information measures. In this paper, we argue that robustness methods based instead on the familiar total variation distance provide simple and more valuable bounds on robustness to misspecification, which are both formally justifiable and transparent. We introduce a novel measure of dependence in conditional probability tables called the diameter to derive such bounds. This measure quantifies the strength of dependence between a variable and its parents. We demonstrate how such formal robustness considerations can be embedded in building a Bayesian network.

Global Sensitivity Analysis of Uncertain Parameters in Bayesian Networks

Traditionally, the sensitivity analysis of a Bayesian network studies the impact of individually modifying the entries of its conditional probability tables in a one-at-a-time (OAT) fashion. However, this approach fails to give a comprehensive account of each inputs' relevance, since simultaneous perturbations in two or more parameters often entail higher-order effects that cannot be captured by an OAT analysis. We propose to conduct global variance-based sensitivity analysis instead, whereby $n$ parameters are viewed as uncertain at once and their importance is assessed jointly. Our method works by encoding the uncertainties as $n$ additional variables of the network. To prevent the curse of dimensionality while adding these dimensions, we use low-rank tensor decomposition to break down the new potentials into smaller factors. Last, we apply the method of Sobol to the resulting network to obtain $n$ global sensitivity indices. Using a benchmark array of both expert-elicited and learned Bayesian networks, we demonstrate that the Sobol indices can significantly differ from the OAT indices, thus revealing the true influence of uncertain parameters and their interactions.

Context-Specific Refinements of Bayesian Network Classifiers

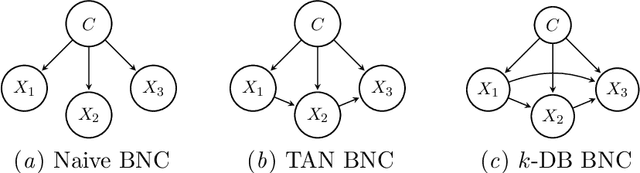
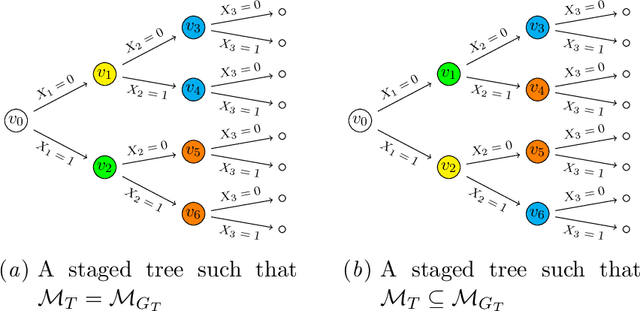
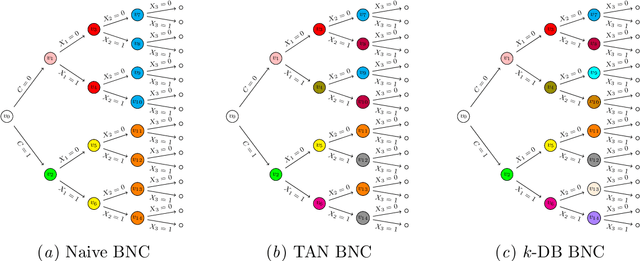
Supervised classification is one of the most ubiquitous tasks in machine learning. Generative classifiers based on Bayesian networks are often used because of their interpretability and competitive accuracy. The widely used naive and TAN classifiers are specific instances of Bayesian network classifiers with a constrained underlying graph. This paper introduces novel classes of generative classifiers extending TAN and other famous types of Bayesian network classifiers. Our approach is based on staged tree models, which extend Bayesian networks by allowing for complex, context-specific patterns of dependence. We formally study the relationship between our novel classes of classifiers and Bayesian networks. We introduce and implement data-driven learning routines for our models and investigate their accuracy in an extensive computational study. The study demonstrates that models embedding asymmetric information can enhance classification accuracy.

Learning Staged Trees from Incomplete Data

Staged trees are probabilistic graphical models capable of representing any class of non-symmetric independence via a coloring of its vertices. Several structural learning routines have been defined and implemented to learn staged trees from data, under the frequentist or Bayesian paradigm. They assume a data set has been observed fully and, in practice, observations with missing entries are either dropped or imputed before learning the model. Here, we introduce the first algorithms for staged trees that handle missingness within the learning of the model. To this end, we characterize the likelihood of staged tree models in the presence of missing data and discuss pseudo-likelihoods that approximate it. A structural expectation-maximization algorithm estimating the model directly from the full likelihood is also implemented and evaluated. A computational experiment showcases the performance of the novel learning algorithms, demonstrating that it is feasible to account for different missingness patterns when learning staged trees.

AI and the creative realm: A short review of current and future applications

This study explores the concept of creativity and artificial intelligence (AI) and their recent integration. While AI has traditionally been perceived as incapable of generating new ideas or creating art, the development of more sophisticated AI models and the proliferation of human-computer interaction tools have opened up new possibilities for AI in artistic creation. This study investigates the various applications of AI in a creative context, differentiating between the type of art, language, and algorithms used. It also considers the philosophical implications of AI and creativity, questioning whether consciousness can be researched in machines and AI's potential interests and decision-making capabilities. Overall, we aim to stimulate a reflection on AI's use and ethical implications in creative contexts.

The YODO algorithm: An efficient computational framework for sensitivity analysis in Bayesian networks

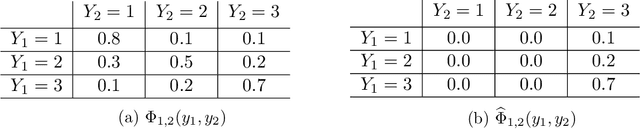
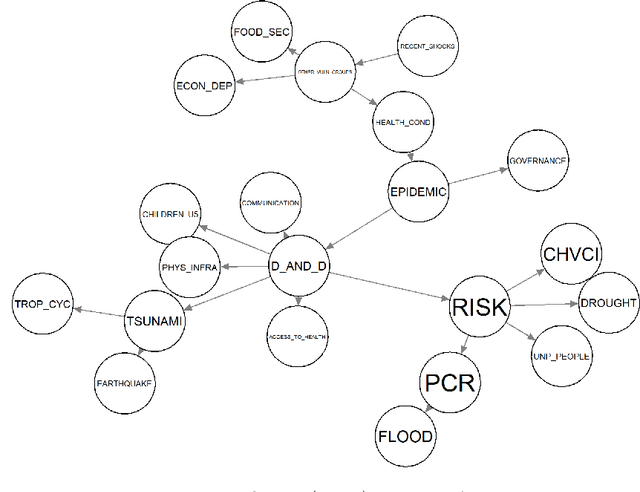
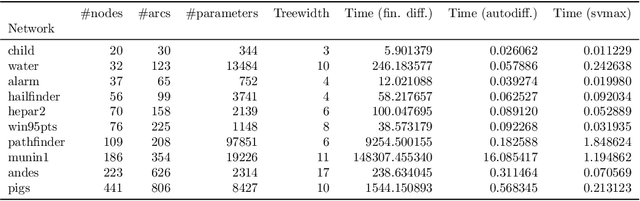
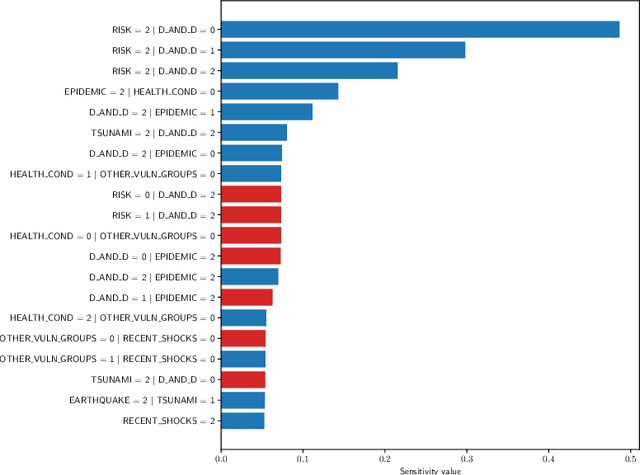
Sensitivity analysis measures the influence of a Bayesian network's parameters on a quantity of interest defined by the network, such as the probability of a variable taking a specific value. Various sensitivity measures have been defined to quantify such influence, most commonly some function of the quantity of interest's partial derivative with respect to the network's conditional probabilities. However, computing these measures in large networks with thousands of parameters can become computationally very expensive. We propose an algorithm combining automatic differentiation and exact inference to efficiently calculate the sensitivity measures in a single pass. It first marginalizes the whole network once, using e.g. variable elimination, and then backpropagates this operation to obtain the gradient with respect to all input parameters. Our method can be used for one-way and multi-way sensitivity analysis and the derivation of admissible regions. Simulation studies highlight the efficiency of our algorithm by scaling it to massive networks with up to 100'000 parameters and investigate the feasibility of generic multi-way analyses. Our routines are also showcased over two medium-sized Bayesian networks: the first modeling the country-risks of a humanitarian crisis, the second studying the relationship between the use of technology and the psychological effects of forced social isolation during the COVID-19 pandemic. An implementation of the methods using the popular machine learning library PyTorch is freely available.

Learning and interpreting asymmetry-labeled DAGs: a case study on COVID-19 fear

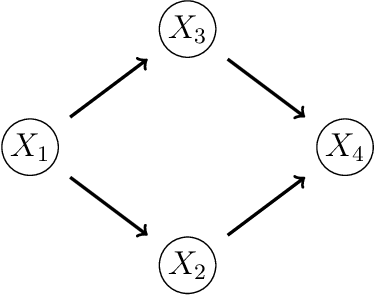
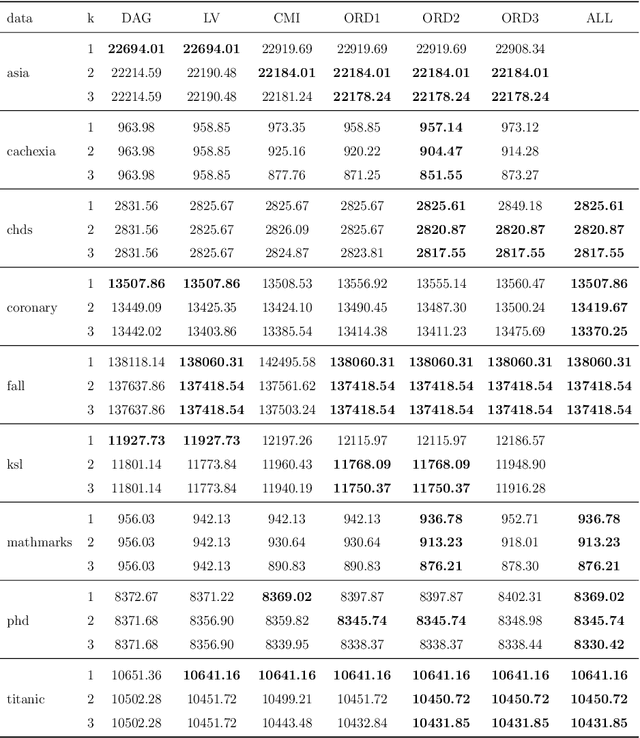
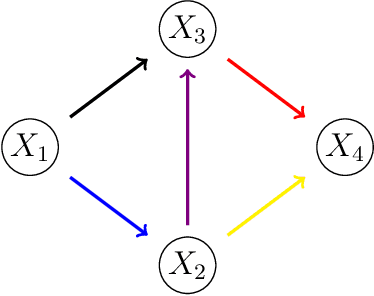
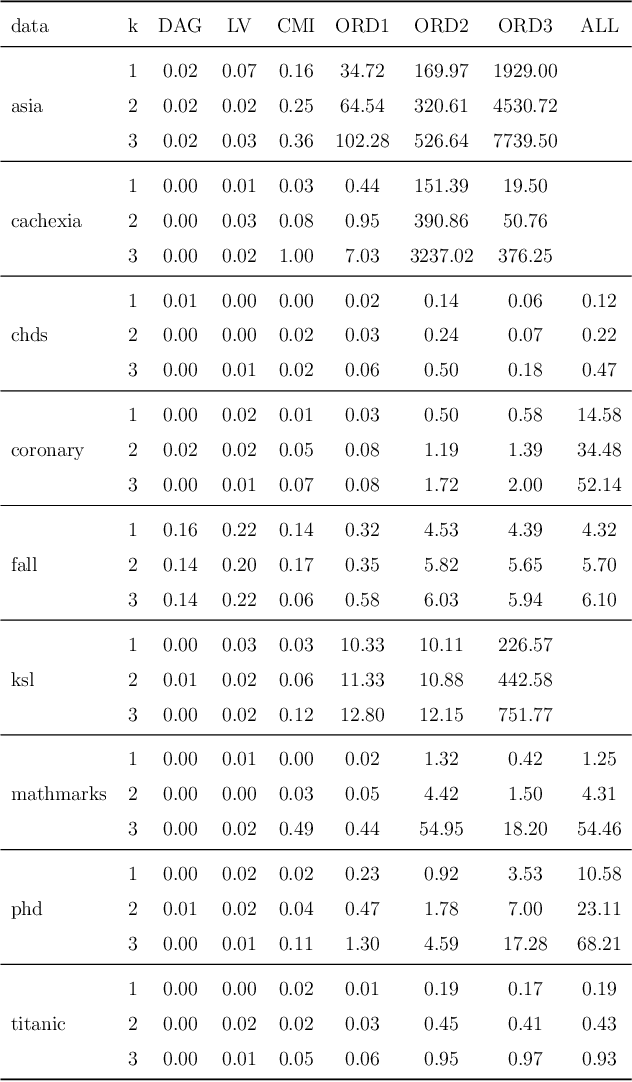
Bayesian networks are widely used to learn and reason about the dependence structure of discrete variables. However, they are only capable of formally encoding symmetric conditional independence, which in practice is often too strict to hold. Asymmetry-labeled DAGs have been recently proposed to both extend the class of Bayesian networks by relaxing the symmetric assumption of independence and denote the type of dependence existing between the variables of interest. Here, we introduce novel structural learning algorithms for this class of models which, whilst being efficient, allow for a straightforward interpretation of the underlying dependence structure. A comprehensive computational study highlights the efficiency of the algorithms. A real-world data application using data from the Fear of COVID-19 Scale collected in Italy showcases their use in practice.

You Only Derive Once (YODO): Automatic Differentiation for Efficient Sensitivity Analysis in Bayesian Networks

Sensitivity analysis measures the influence of a Bayesian network's parameters on a quantity of interest defined by the network, such as the probability of a variable taking a specific value. In particular, the so-called sensitivity value measures the quantity of interest's partial derivative with respect to the network's conditional probabilities. However, finding such values in large networks with thousands of parameters can become computationally very expensive. We propose to use automatic differentiation combined with exact inference to obtain all sensitivity values in a single pass. Our method first marginalizes the whole network once using e.g. variable elimination and then backpropagates this operation to obtain the gradient with respect to all input parameters. We demonstrate our routines by ranking all parameters by importance on a Bayesian network modeling humanitarian crises and disasters, and then show the method's efficiency by scaling it to huge networks with up to 100'000 parameters. An implementation of the methods using the popular machine learning library PyTorch is freely available.

Highly Efficient Structural Learning of Sparse Staged Trees

Several structural learning algorithms for staged tree models, an asymmetric extension of Bayesian networks, have been defined. However, they do not scale efficiently as the number of variables considered increases. Here we introduce the first scalable structural learning algorithm for staged trees, which searches over a space of models where only a small number of dependencies can be imposed. A simulation study as well as a real-world application illustrate our routines and the practical use of such data-learned staged trees.