Global Sensitivity Analysis of Uncertain Parameters in Bayesian Networks

Traditionally, the sensitivity analysis of a Bayesian network studies the impact of individually modifying the entries of its conditional probability tables in a one-at-a-time (OAT) fashion. However, this approach fails to give a comprehensive account of each inputs' relevance, since simultaneous perturbations in two or more parameters often entail higher-order effects that cannot be captured by an OAT analysis. We propose to conduct global variance-based sensitivity analysis instead, whereby $n$ parameters are viewed as uncertain at once and their importance is assessed jointly. Our method works by encoding the uncertainties as $n$ additional variables of the network. To prevent the curse of dimensionality while adding these dimensions, we use low-rank tensor decomposition to break down the new potentials into smaller factors. Last, we apply the method of Sobol to the resulting network to obtain $n$ global sensitivity indices. Using a benchmark array of both expert-elicited and learned Bayesian networks, we demonstrate that the Sobol indices can significantly differ from the OAT indices, thus revealing the true influence of uncertain parameters and their interactions.

The YODO algorithm: An efficient computational framework for sensitivity analysis in Bayesian networks

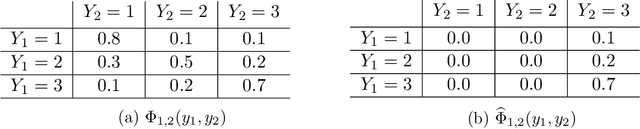
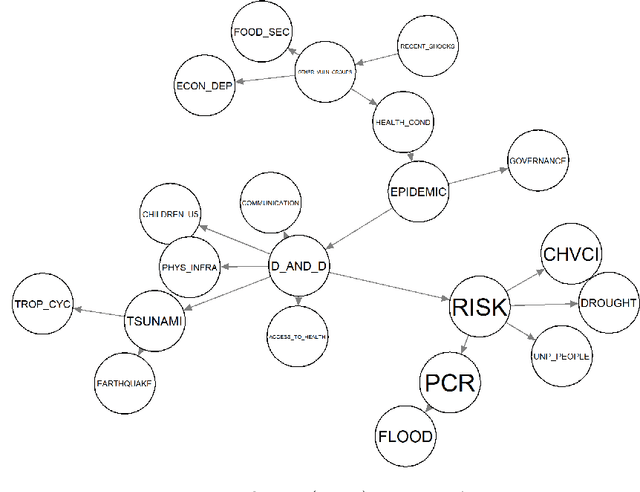
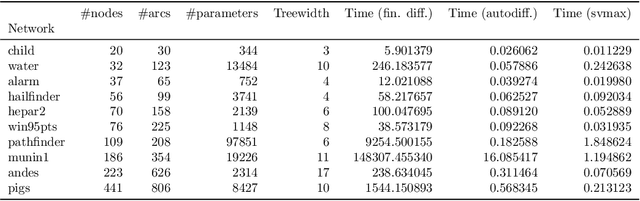
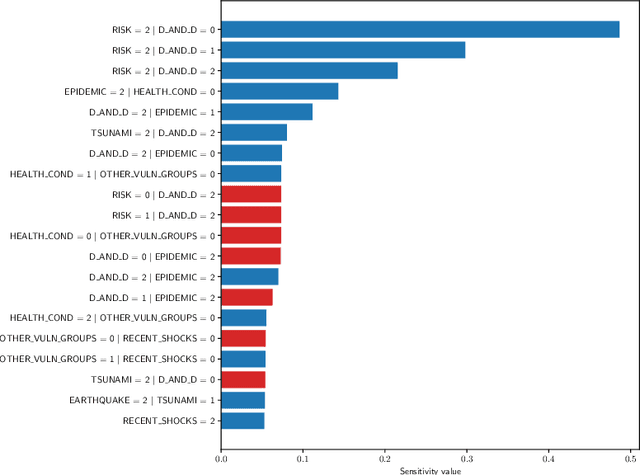
Sensitivity analysis measures the influence of a Bayesian network's parameters on a quantity of interest defined by the network, such as the probability of a variable taking a specific value. Various sensitivity measures have been defined to quantify such influence, most commonly some function of the quantity of interest's partial derivative with respect to the network's conditional probabilities. However, computing these measures in large networks with thousands of parameters can become computationally very expensive. We propose an algorithm combining automatic differentiation and exact inference to efficiently calculate the sensitivity measures in a single pass. It first marginalizes the whole network once, using e.g. variable elimination, and then backpropagates this operation to obtain the gradient with respect to all input parameters. Our method can be used for one-way and multi-way sensitivity analysis and the derivation of admissible regions. Simulation studies highlight the efficiency of our algorithm by scaling it to massive networks with up to 100'000 parameters and investigate the feasibility of generic multi-way analyses. Our routines are also showcased over two medium-sized Bayesian networks: the first modeling the country-risks of a humanitarian crisis, the second studying the relationship between the use of technology and the psychological effects of forced social isolation during the COVID-19 pandemic. An implementation of the methods using the popular machine learning library PyTorch is freely available.

tntorch: Tensor Network Learning with PyTorch

We present tntorch, a tensor learning framework that supports multiple decompositions (including Candecomp/Parafac, Tucker, and Tensor Train) under a unified interface. With our library, the user can learn and handle low-rank tensors with automatic differentiation, seamless GPU support, and the convenience of PyTorch's API. Besides decomposition algorithms, tntorch implements differentiable tensor algebra, rank truncation, cross-approximation, batch processing, comprehensive tensor arithmetics, and more.

You Only Derive Once (YODO): Automatic Differentiation for Efficient Sensitivity Analysis in Bayesian Networks

Sensitivity analysis measures the influence of a Bayesian network's parameters on a quantity of interest defined by the network, such as the probability of a variable taking a specific value. In particular, the so-called sensitivity value measures the quantity of interest's partial derivative with respect to the network's conditional probabilities. However, finding such values in large networks with thousands of parameters can become computationally very expensive. We propose to use automatic differentiation combined with exact inference to obtain all sensitivity values in a single pass. Our method first marginalizes the whole network once using e.g. variable elimination and then backpropagates this operation to obtain the gradient with respect to all input parameters. We demonstrate our routines by ranking all parameters by importance on a Bayesian network modeling humanitarian crises and disasters, and then show the method's efficiency by scaling it to huge networks with up to 100'000 parameters. An implementation of the methods using the popular machine learning library PyTorch is freely available.

Are Quantum Computers Practical Yet? A Case for Feature Selection in Recommender Systems using Tensor Networks

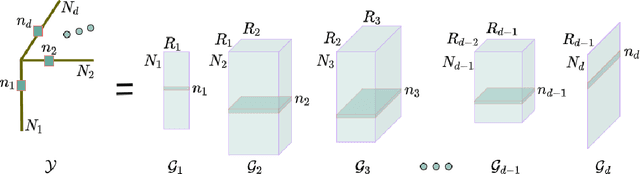
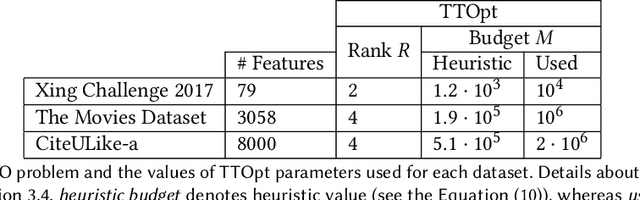
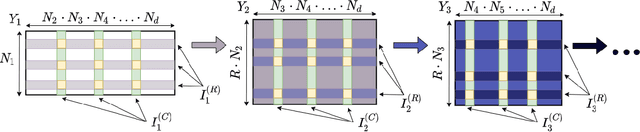
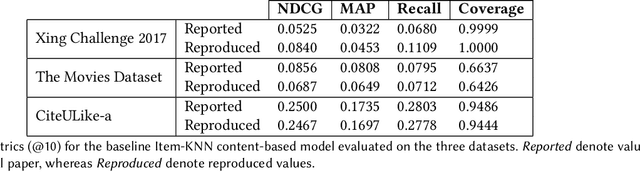
Collaborative filtering models generally perform better than content-based filtering models and do not require careful feature engineering. However, in the cold-start scenario collaborative information may be scarce or even unavailable, whereas the content information may be abundant, but also noisy and expensive to acquire. Thus, selection of particular features that improve cold-start recommendations becomes an important and non-trivial task. In the recent approach by Nembrini et al., the feature selection is driven by the correlational compatibility between collaborative and content-based models. The problem is formulated as a Quadratic Unconstrained Binary Optimization (QUBO) which, due to its NP-hard complexity, is solved using Quantum Annealing on a quantum computer provided by D-Wave. Inspired by the reported results, we contend the idea that current quantum annealers are superior for this problem and instead focus on classical algorithms. In particular, we tackle QUBO via TTOpt, a recently proposed black-box optimizer based on tensor networks and multilinear algebra. We show the computational feasibility of this method for large problems with thousands of features, and empirically demonstrate that the solutions found are comparable to the ones obtained with D-Wave across all examined datasets.

Global sensitivity analysis in probabilistic graphical models

We show how to apply Sobol's method of global sensitivity analysis to measure the influence exerted by a set of nodes' evidence on a quantity of interest expressed by a Bayesian network. Our method exploits the network structure so as to transform the problem of Sobol index estimation into that of marginalization inference. This way, we can efficiently compute indices for networks where brute-force or Monte Carlo based estimators for variance-based sensitivity analysis would require millions of costly samples. Moreover, our method gives exact results when exact inference is used, and also supports the case of correlated inputs. The proposed algorithm is inspired by the field of tensor networks, and generalizes earlier tensor sensitivity techniques from the acyclic to the cyclic case. We demonstrate the method on three medium to large Bayesian networks that cover the areas of project risk management and reliability engineering.

Cherry-Picking Gradients: Learning Low-Rank Embeddings of Visual Data via Differentiable Cross-Approximation

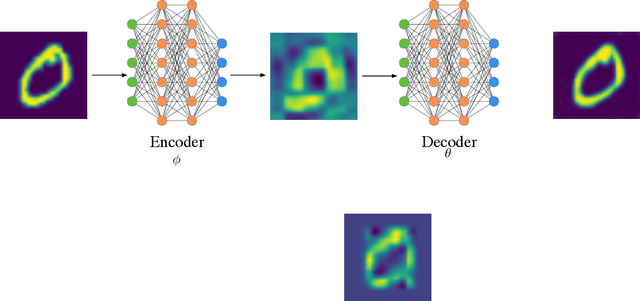
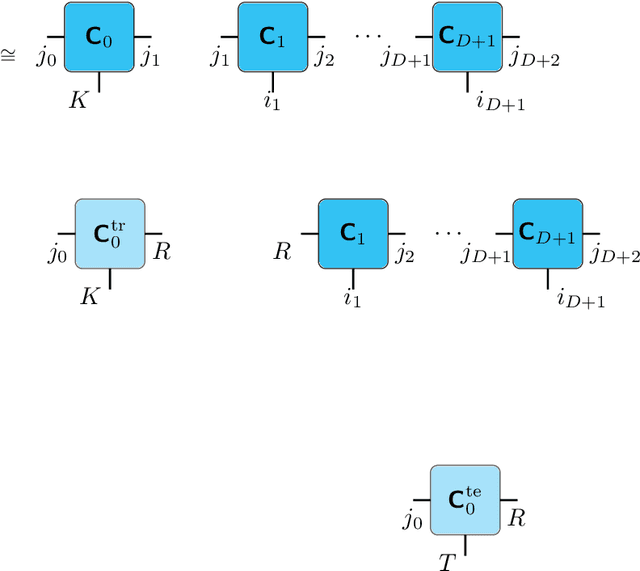
We propose an end-to-end trainable framework that processes large-scale visual data tensors by looking \emph{at a fraction of their entries only}. Our method combines a neural network encoder with a \emph{tensor train decomposition} to learn a low-rank latent encoding, coupled with cross-approximation (CA) to learn the representation through a subset of the original samples. CA is an adaptive sampling algorithm that is native to tensor decompositions and avoids working with the full high-resolution data explicitly. Instead, it actively selects local representative samples that we fetch out-of-core and on-demand. The required number of samples grows only logarithmically with the size of the input. Our implicit representation of the tensor in the network enables processing large grids that could not be otherwise tractable in their uncompressed form. The proposed approach is particularly useful for large-scale multidimensional grid data (e.g., 3D tomography), and for tasks that require context over a large receptive field (e.g., predicting the medical condition of entire organs). The code will be available at https://github.com/aelphy/c-pic

Visualization of High-dimensional Scalar Functions Using Principal Parameterizations

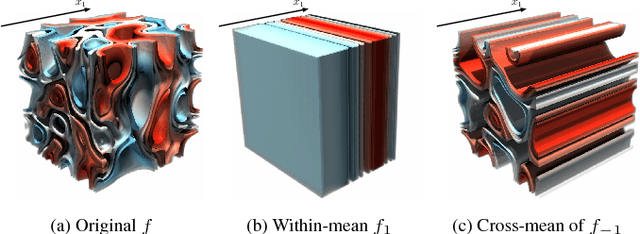
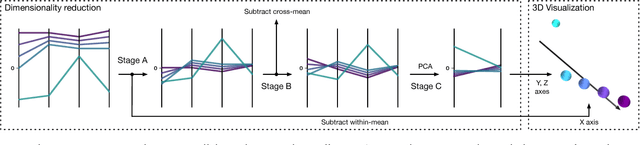
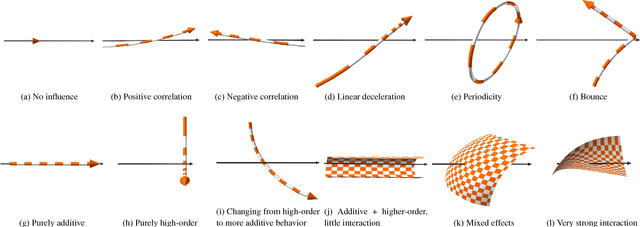
Insightful visualization of multidimensional scalar fields, in particular parameter spaces, is key to many fields in computational science and engineering. We propose a principal component-based approach to visualize such fields that accurately reflects their sensitivity to input parameters. The method performs dimensionality reduction on the vast $L^2$ Hilbert space formed by all possible partial functions (i.e., those defined by fixing one or more input parameters to specific values), which are projected to low-dimensional parameterized manifolds such as 3D curves, surfaces, and ensembles thereof. Our mapping provides a direct geometrical and visual interpretation in terms of Sobol's celebrated method for variance-based sensitivity analysis. We furthermore contribute a practical realization of the proposed method by means of tensor decomposition, which enables accurate yet interactive integration and multilinear principal component analysis of high-dimensional models.