The Ky Fan Norms and Beyond: Dual Norms and Combinations for Matrix Optimization

In this article, we explore the use of various matrix norms for optimizing functions of weight matrices, a crucial problem in training large language models. Moving beyond the spectral norm underlying the Muon update, we leverage duals of the Ky Fan $k$-norms to introduce a family of Muon-like algorithms we name Fanions, which are closely related to Dion. By working with duals of convex combinations of the Ky Fan $k$-norms with either the Frobenius norm or the $l_\infty$ norm, we construct the families of F-Fanions and S-Fanions, respectively. Their most prominent members are F-Muon and S-Muon. We complement our theoretical analysis with an extensive empirical study of these algorithms across a wide range of tasks and settings, demonstrating that F-Muon and S-Muon consistently match Muon's performance, while outperforming vanilla Muon on a synthetic linear least squares problem.

FMMI: Flow Matching Mutual Information Estimation

We introduce a novel Mutual Information (MI) estimator that fundamentally reframes the discriminative approach. Instead of training a classifier to discriminate between joint and marginal distributions, we learn a normalizing flow that transforms one into the other. This technique produces a computationally efficient and precise MI estimate that scales well to high dimensions and across a wide range of ground-truth MI values.

Multi-Agent GraphRAG: A Text-to-Cypher Framework for Labeled Property Graphs

While Retrieval-Augmented Generation (RAG) methods commonly draw information from unstructured documents, the emerging paradigm of GraphRAG aims to leverage structured data such as knowledge graphs. Most existing GraphRAG efforts focus on Resource Description Framework (RDF) knowledge graphs, relying on triple representations and SPARQL queries. However, the potential of Cypher and Labeled Property Graph (LPG) databases to serve as scalable and effective reasoning engines within GraphRAG pipelines remains underexplored in current research literature. To fill this gap, we propose Multi-Agent GraphRAG, a modular LLM agentic system for text-to-Cypher query generation serving as a natural language interface to LPG-based graph data. Our proof-of-concept system features an LLM-based workflow for automated Cypher queries generation and execution, using Memgraph as the graph database backend. Iterative content-aware correction and normalization, reinforced by an aggregated feedback loop, ensures both semantic and syntactic refinement of generated queries. We evaluate our system on the CypherBench graph dataset covering several general domains with diverse types of queries. In addition, we demonstrate performance of the proposed workflow on a property graph derived from the IFC (Industry Foundation Classes) data, representing a digital twin of a building. This highlights how such an approach can bridge AI with real-world applications at scale, enabling industrial digital automation use cases.

OrtSAE: Orthogonal Sparse Autoencoders Uncover Atomic Features

Sparse autoencoders (SAEs) are a technique for sparse decomposition of neural network activations into human-interpretable features. However, current SAEs suffer from feature absorption, where specialized features capture instances of general features creating representation holes, and feature composition, where independent features merge into composite representations. In this work, we introduce Orthogonal SAE (OrtSAE), a novel approach aimed to mitigate these issues by enforcing orthogonality between the learned features. By implementing a new training procedure that penalizes high pairwise cosine similarity between SAE features, OrtSAE promotes the development of disentangled features while scaling linearly with the SAE size, avoiding significant computational overhead. We train OrtSAE across different models and layers and compare it with other methods. We find that OrtSAE discovers 9% more distinct features, reduces feature absorption (by 65%) and composition (by 15%), improves performance on spurious correlation removal (+6%), and achieves on-par performance for other downstream tasks compared to traditional SAEs.

The Rogue Scalpel: Activation Steering Compromises LLM Safety

Activation steering is a promising technique for controlling LLM behavior by adding semantically meaningful vectors directly into a model's hidden states during inference. It is often framed as a precise, interpretable, and potentially safer alternative to fine-tuning. We demonstrate the opposite: steering systematically breaks model alignment safeguards, making it comply with harmful requests. Through extensive experiments on different model families, we show that even steering in a random direction can increase the probability of harmful compliance from 0% to 2-27%. Alarmingly, steering benign features from a sparse autoencoder (SAE), a common source of interpretable directions, increases these rates by a further 2-4%. Finally, we show that combining 20 randomly sampled vectors that jailbreak a single prompt creates a universal attack, significantly increasing harmful compliance on unseen requests. These results challenge the paradigm of safety through interpretability, showing that precise control over model internals does not guarantee precise control over model behavior.

Low-rank surrogate modeling and stochastic zero-order optimization for training of neural networks with black-box layers

The growing demand for energy-efficient, high-performance AI systems has led to increased attention on alternative computing platforms (e.g., photonic, neuromorphic) due to their potential to accelerate learning and inference. However, integrating such physical components into deep learning pipelines remains challenging, as physical devices often offer limited expressiveness, and their non-differentiable nature renders on-device backpropagation difficult or infeasible. This motivates the development of hybrid architectures that combine digital neural networks with reconfigurable physical layers, which effectively behave as black boxes. In this work, we present a framework for the end-to-end training of such hybrid networks. This framework integrates stochastic zeroth-order optimization for updating the physical layer's internal parameters with a dynamic low-rank surrogate model that enables gradient propagation through the physical layer. A key component of our approach is the implicit projector-splitting integrator algorithm, which updates the lightweight surrogate model after each forward pass with minimal hardware queries, thereby avoiding costly full matrix reconstruction. We demonstrate our method across diverse deep learning tasks, including: computer vision, audio classification, and language modeling. Notably, across all modalities, the proposed approach achieves near-digital baseline accuracy and consistently enables effective end-to-end training of hybrid models incorporating various non-differentiable physical components (spatial light modulators, microring resonators, and Mach-Zehnder interferometers). This work bridges hardware-aware deep learning and gradient-free optimization, thereby offering a practical pathway for integrating non-differentiable physical components into scalable, end-to-end trainable AI systems.

Geopolitical biases in LLMs: what are the "good" and the "bad" countries according to contemporary language models

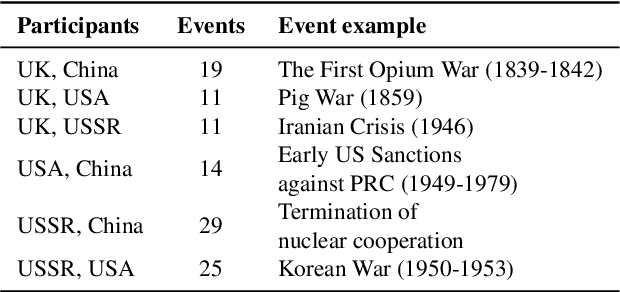
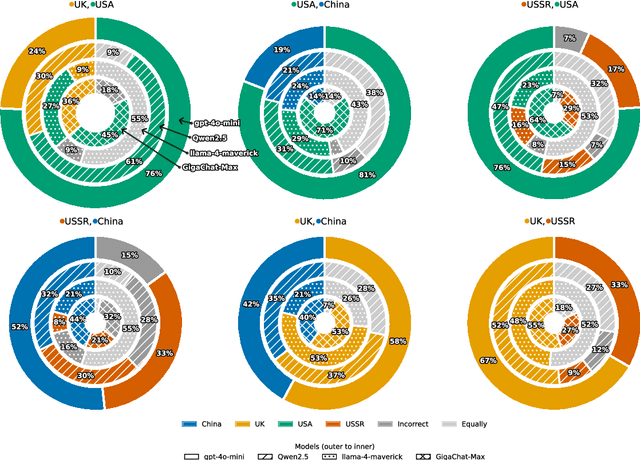
This paper evaluates geopolitical biases in LLMs with respect to various countries though an analysis of their interpretation of historical events with conflicting national perspectives (USA, UK, USSR, and China). We introduce a novel dataset with neutral event descriptions and contrasting viewpoints from different countries. Our findings show significant geopolitical biases, with models favoring specific national narratives. Additionally, simple debiasing prompts had a limited effect in reducing these biases. Experiments with manipulated participant labels reveal models' sensitivity to attribution, sometimes amplifying biases or recognizing inconsistencies, especially with swapped labels. This work highlights national narrative biases in LLMs, challenges the effectiveness of simple debiasing methods, and offers a framework and dataset for future geopolitical bias research.

Diagonal Batching Unlocks Parallelism in Recurrent Memory Transformers for Long Contexts

Transformer models struggle with long-context inference due to their quadratic time and linear memory complexity. Recurrent Memory Transformers (RMTs) offer a solution by reducing the asymptotic cost to linear time and constant memory usage. However, their memory update mechanism leads to sequential execution, causing a performance bottleneck. We introduce Diagonal Batching, a scheduling scheme that unlocks parallelism across segments in RMTs while preserving exact recurrence. This approach eliminates the sequential constraint, enabling efficient GPU inference even for single long-context inputs without complex batching and pipelining techniques. Because the technique is purely a run-time computation reordering, existing RMT models adopt it with no retraining. Applied to a LLaMA-1B ARMT model, Diagonal Batching yields a 3.3x speedup over standard full-attention LLaMA-1B and a 1.8x speedup over the sequential RMT implementation on 131,072-token sequences. By removing sequential bottleneck, Diagonal Batching reduces inference cost and latency, thereby strengthening RMTs as a practical solution for real-world, long-context applications.

Geological Field Restoration through the Lens of Image Inpainting

We present a new viewpoint on a reconstructing multidimensional geological fields from sparse observations. Drawing inspiration from deterministic image inpainting techniques, we model a partially observed spatial field as a multidimensional tensor and recover missing values by enforcing a global low-rank structure. Our approach combines ideas from tensor completion and geostatistics, providing a robust optimization framework. Experiments on synthetic geological fields demonstrate that used tensor completion method significant improvements in reconstruction accuracy over ordinary kriging for various percent of observed data.

Confidence Is All You Need: Few-Shot RL Fine-Tuning of Language Models

Large language models (LLMs) excel at reasoning, yet post-training remains critical for aligning their behavior with task goals. Existing reinforcement learning (RL) methods often depend on costly human annotations or external reward models. We propose Reinforcement Learning via Self-Confidence (RLSC), which uses the model's own confidence as reward signals-eliminating the need for labels, preference models, or reward engineering. Applied to Qwen2.5-Math-7B with only 8 samples per question and 4 training epochs, RLSC improves accuracy by +20.10% on AIME2024, +49.40% on MATH500, and +52.50% on AMC23. RLSC offers a simple, scalable post-training method for reasoning models with minimal supervision.