Can message-passing GNN approximate triangular factorizations of sparse matrices?

We study fundamental limitations of Graph Neural Networks (GNNs) for learning sparse matrix preconditioners. While recent works have shown promising results using GNNs to predict incomplete factorizations, we demonstrate that the local nature of message passing creates inherent barriers for capturing non-local dependencies required for optimal preconditioning. We introduce a new benchmark dataset of matrices where good sparse preconditioners exist but require non-local computations, constructed using both synthetic examples and real-world matrices. Our experimental results show that current GNN architectures struggle to approximate these preconditioners, suggesting the need for new architectural approaches beyond traditional message passing networks. We provide theoretical analysis and empirical evidence to explain these limitations, with implications for the broader use of GNNs in numerical linear algebra.

ConDiff: A Challenging Dataset for Neural Solvers of Partial Differential Equations

We present ConDiff, a novel dataset for scientific machine learning. ConDiff focuses on the diffusion equation with varying coefficients, a fundamental problem in many applications of parametric partial differential equations (PDEs). The main novelty of the proposed dataset is that we consider discontinuous coefficients with high contrast. These coefficient functions are sampled from a selected set of distributions. This class of problems is not only of great academic interest, but is also the basis for describing various environmental and industrial problems. In this way, ConDiff shortens the gap with real-world problems while remaining fully synthetic and easy to use. ConDiff consists of a diverse set of diffusion equations with coefficients covering a wide range of contrast levels and heterogeneity with a measurable complexity metric for clearer comparison between different coefficient functions. We baseline ConDiff on standard deep learning models in the field of scientific machine learning. By providing a large number of problem instances, each with its own coefficient function and right-hand side, we hope to encourage the development of novel physics-based deep learning approaches, such as neural operators and physics-informed neural networks, ultimately driving progress towards more accurate and efficient solutions of complex PDE problems.

Learning from Linear Algebra: A Graph Neural Network Approach to Preconditioner Design for Conjugate Gradient Solvers

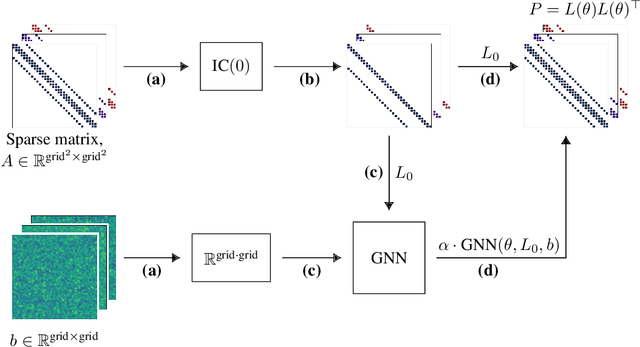
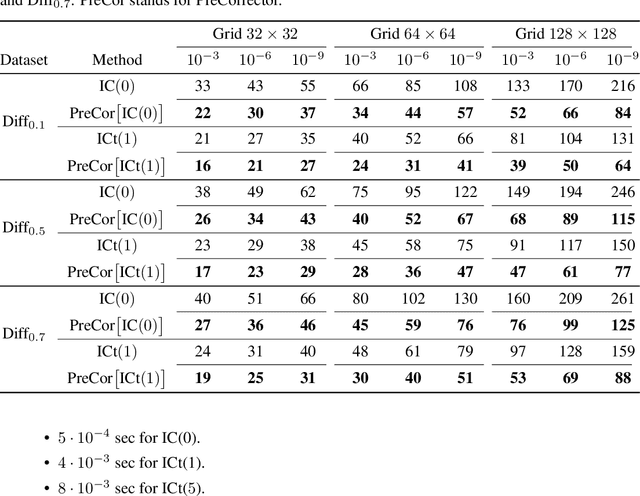
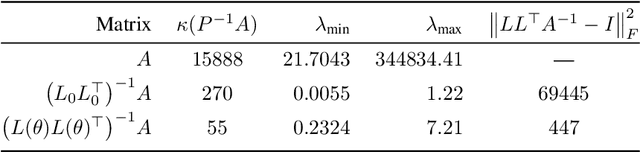
Large linear systems are ubiquitous in modern computational science. The main recipe for solving them is iterative solvers with well-designed preconditioners. Deep learning models may be used to precondition residuals during iteration of such linear solvers as the conjugate gradient (CG) method. Neural network models require an enormous number of parameters to approximate well in this setup. Another approach is to take advantage of small graph neural networks (GNNs) to construct preconditioners of the predefined sparsity pattern. In our work, we recall well-established preconditioners from linear algebra and use them as a starting point for training the GNN. Numerical experiments demonstrate that our approach outperforms both classical methods and neural network-based preconditioning. We also provide a heuristic justification for the loss function used and validate our approach on complex datasets.

Quantization of Large Language Models with an Overdetermined Basis

In this paper, we introduce an algorithm for data quantization based on the principles of Kashin representation. This approach hinges on decomposing any given vector, matrix, or tensor into two factors. The first factor maintains a small infinity norm, while the second exhibits a similarly constrained norm when multiplied by an orthogonal matrix. Surprisingly, the entries of factors after decomposition are well-concentrated around several peaks, which allows us to efficiently replace them with corresponding centroids for quantization purposes. We study the theoretical properties of the proposed approach and rigorously evaluate our compression algorithm in the context of next-word prediction tasks and on a set of downstream tasks for text classification. Our findings demonstrate that Kashin Quantization achieves competitive or superior quality in model performance while ensuring data compression, marking a significant advancement in the field of data quantization.

Reconstruction of 3D Porous Media From 2D Slices

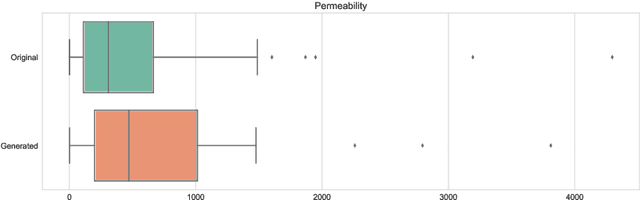
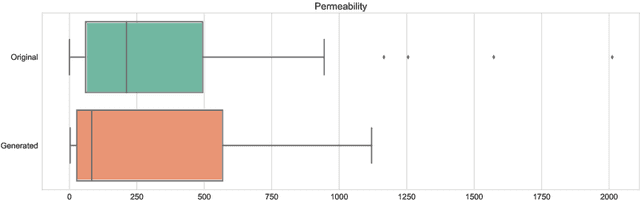
We propose a novel deep learning architecture for three-dimensional porous media structure reconstruction from two-dimensional slices. A high-level idea is that we fit a distribution on all possible three-dimensional structures of a specific type based on the given dataset of samples. Then, given partial information (central slices) we recover the three-dimensional structure that is built around such slices. Technically, it is implemented as a deep neural network with encoder, generator and discriminator modules. Numerical experiments show that this method gives a good reconstruction in terms of Minkowski functionals.

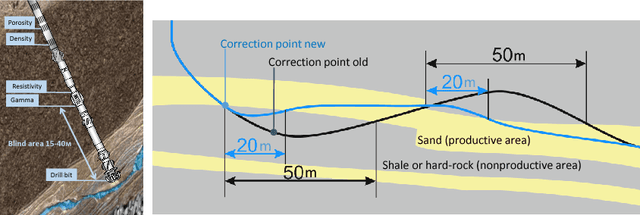
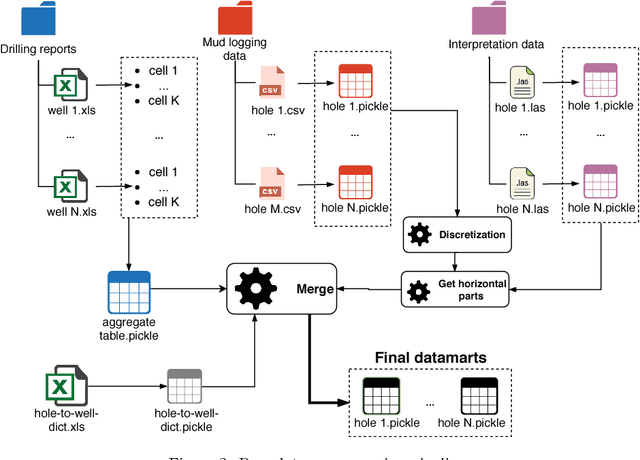
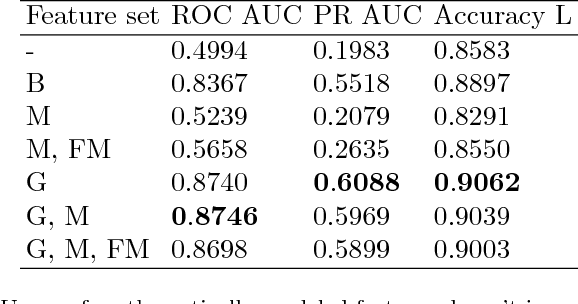
Data-driven model for the identification of the rock type at a drilling bit

In order to bridge the gap of more than 15m between the drilling bit and high-fidelity rock type sensors during the directional drilling, we present a novel approach for identifying rock type at the drilling bit. The approach is based on application of machine learning techniques for Measurements While Drilling (MWD) data. We demonstrate capabilities of the developed approach for distinguishing between the rock types corresponding to (1) a target oil bearing interval of a reservoir and (2) a non-productive shale layer and compare it to more traditional physics-driven approaches. The dataset includes MWD data and lithology mapping along multiple wellbores obtained by processing of Logging While Drilling (LWD) measurements from a massive drilling effort on one of the major newly developed oilfield in the North of Western Siberia. We compare various machine-learning algorithms, examine extra features coming from physical modeling of drilling mechanics, and show that the classification error can be reduced from 13.5% to 9%.