ConDiff: A Challenging Dataset for Neural Solvers of Partial Differential Equations

We present ConDiff, a novel dataset for scientific machine learning. ConDiff focuses on the diffusion equation with varying coefficients, a fundamental problem in many applications of parametric partial differential equations (PDEs). The main novelty of the proposed dataset is that we consider discontinuous coefficients with high contrast. These coefficient functions are sampled from a selected set of distributions. This class of problems is not only of great academic interest, but is also the basis for describing various environmental and industrial problems. In this way, ConDiff shortens the gap with real-world problems while remaining fully synthetic and easy to use. ConDiff consists of a diverse set of diffusion equations with coefficients covering a wide range of contrast levels and heterogeneity with a measurable complexity metric for clearer comparison between different coefficient functions. We baseline ConDiff on standard deep learning models in the field of scientific machine learning. By providing a large number of problem instances, each with its own coefficient function and right-hand side, we hope to encourage the development of novel physics-based deep learning approaches, such as neural operators and physics-informed neural networks, ultimately driving progress towards more accurate and efficient solutions of complex PDE problems.

Learning from Linear Algebra: A Graph Neural Network Approach to Preconditioner Design for Conjugate Gradient Solvers

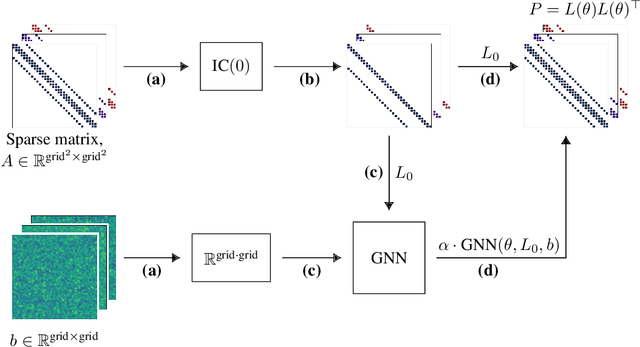
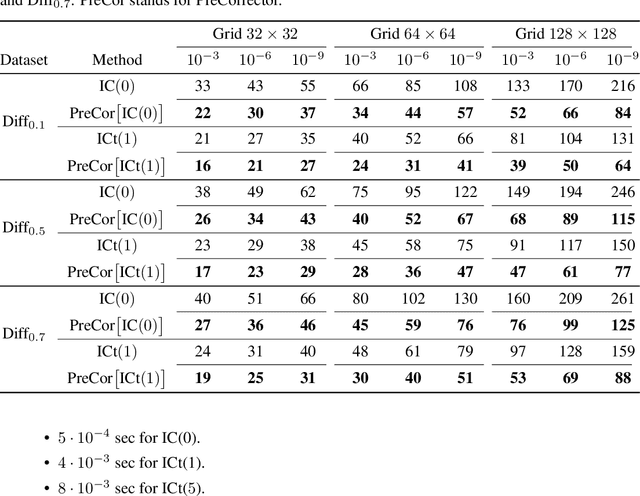
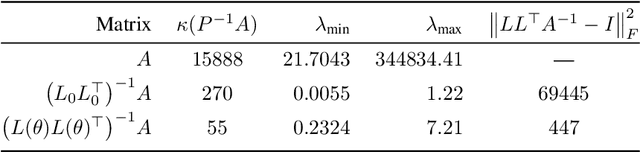
Large linear systems are ubiquitous in modern computational science. The main recipe for solving them is iterative solvers with well-designed preconditioners. Deep learning models may be used to precondition residuals during iteration of such linear solvers as the conjugate gradient (CG) method. Neural network models require an enormous number of parameters to approximate well in this setup. Another approach is to take advantage of small graph neural networks (GNNs) to construct preconditioners of the predefined sparsity pattern. In our work, we recall well-established preconditioners from linear algebra and use them as a starting point for training the GNN. Numerical experiments demonstrate that our approach outperforms both classical methods and neural network-based preconditioning. We also provide a heuristic justification for the loss function used and validate our approach on complex datasets.

Machine learning methods for prediction of breakthrough curves in reactive porous media

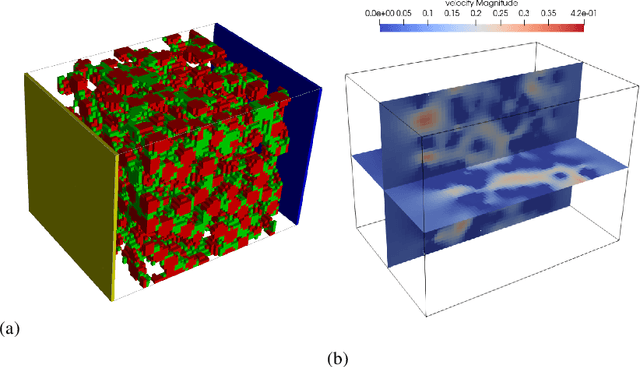
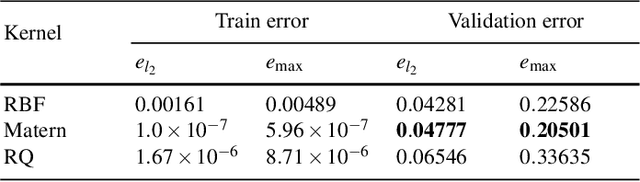
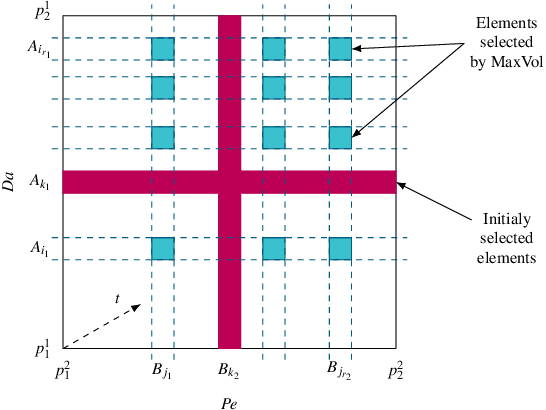
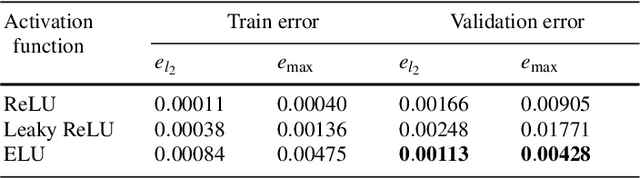
Reactive flows in porous media play an important role in our life and are crucial for many industrial, environmental and biomedical applications. Very often the concentration of the species at the inlet is known, and the so-called breakthrough curves, measured at the outlet, are the quantities which could be measured or computed numerically. The measurements and the simulations could be time-consuming and expensive, and machine learning and Big Data approaches can help to predict breakthrough curves at lower costs. Machine learning (ML) methods, such as Gaussian processes and fully-connected neural networks, and a tensor method, cross approximation, are well suited for predicting breakthrough curves. In this paper, we demonstrate their performance in the case of pore scale reactive flow in catalytic filters.

On the Performance of Machine Learning Methods for Breakthrough Curve Prediction

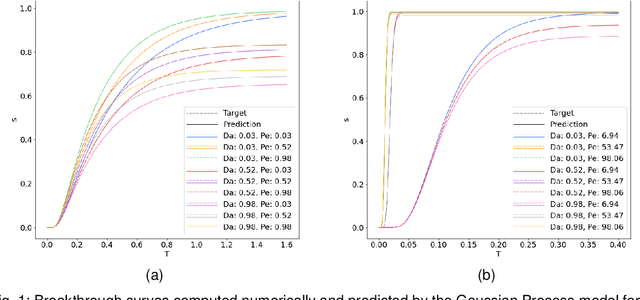
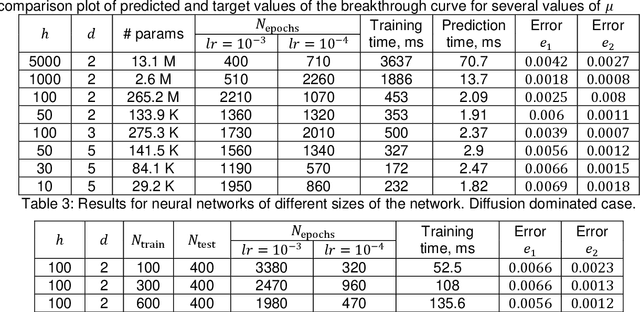
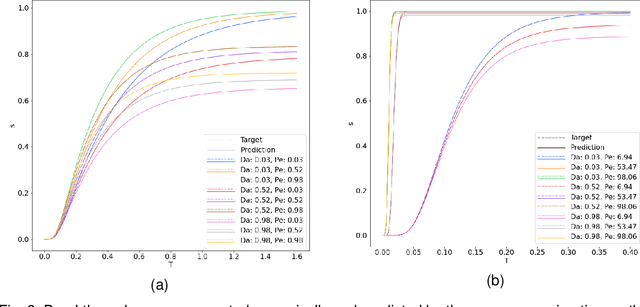
Reactive flows are important part of numerous technical and environmental processes. Often monitoring the flow and species concentrations within the domain is not possible or is expensive, in contrast, outlet concentration is straightforward to measure. In connection with reactive flows in porous media, the term breakthrough curve is used to denote the time dependency of the outlet concentration with prescribed conditions at the inlet. In this work we apply several machine learning methods to predict breakthrough curves from the given set of parameters. In our case the parameters are the Damk\"ohler and Peclet numbers. We perform a thorough analysis for the one-dimensional case and also provide the results for the three-dimensional case.