Machine learning methods for prediction of breakthrough curves in reactive porous media

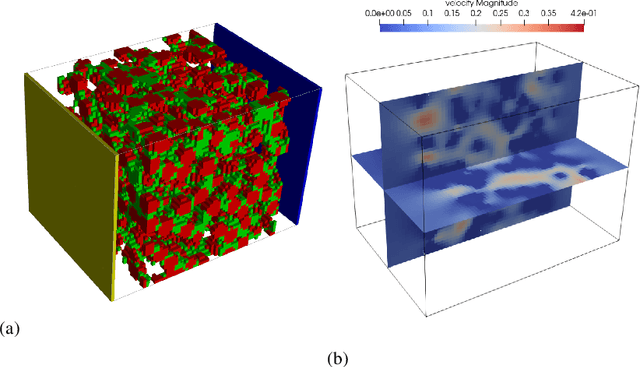
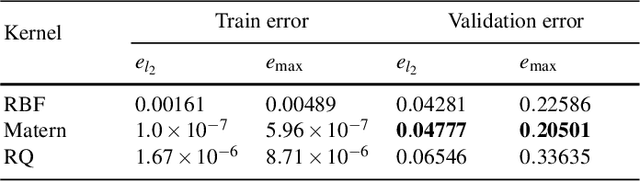
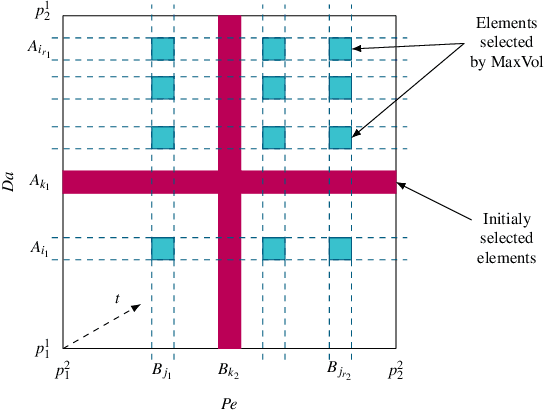
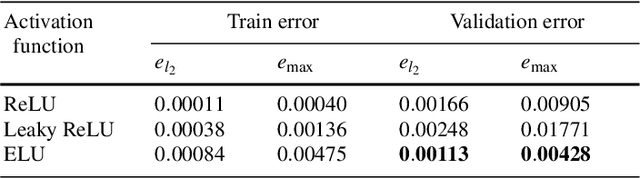
Reactive flows in porous media play an important role in our life and are crucial for many industrial, environmental and biomedical applications. Very often the concentration of the species at the inlet is known, and the so-called breakthrough curves, measured at the outlet, are the quantities which could be measured or computed numerically. The measurements and the simulations could be time-consuming and expensive, and machine learning and Big Data approaches can help to predict breakthrough curves at lower costs. Machine learning (ML) methods, such as Gaussian processes and fully-connected neural networks, and a tensor method, cross approximation, are well suited for predicting breakthrough curves. In this paper, we demonstrate their performance in the case of pore scale reactive flow in catalytic filters.

On the Performance of Machine Learning Methods for Breakthrough Curve Prediction

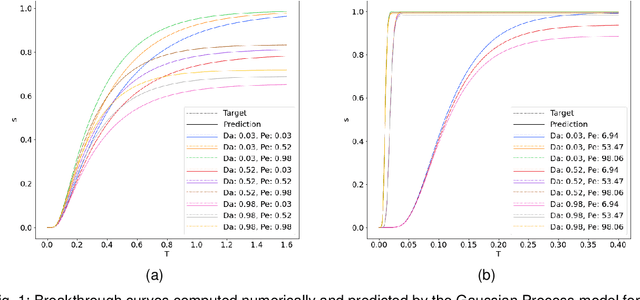
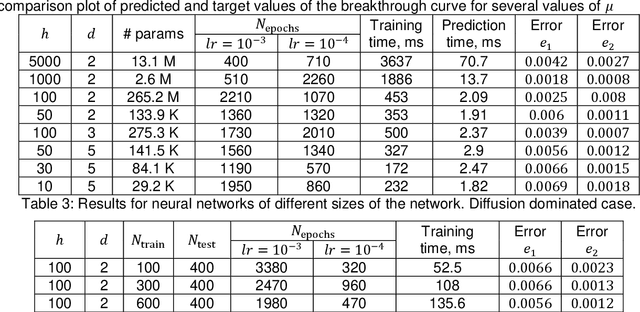
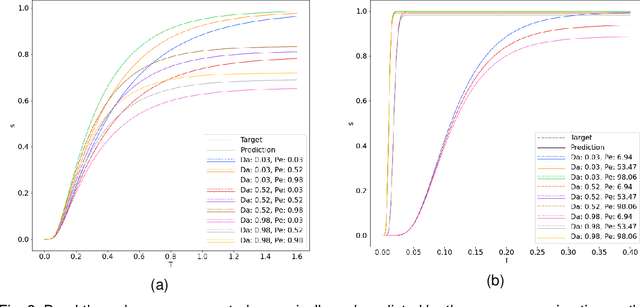
Reactive flows are important part of numerous technical and environmental processes. Often monitoring the flow and species concentrations within the domain is not possible or is expensive, in contrast, outlet concentration is straightforward to measure. In connection with reactive flows in porous media, the term breakthrough curve is used to denote the time dependency of the outlet concentration with prescribed conditions at the inlet. In this work we apply several machine learning methods to predict breakthrough curves from the given set of parameters. In our case the parameters are the Damk\"ohler and Peclet numbers. We perform a thorough analysis for the one-dimensional case and also provide the results for the three-dimensional case.

Growing axons: greedy learning of neural networks with application to function approximation

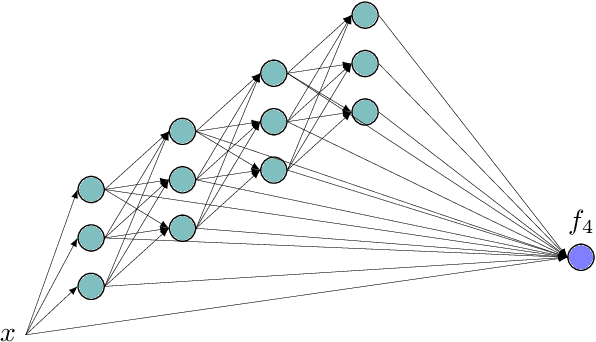
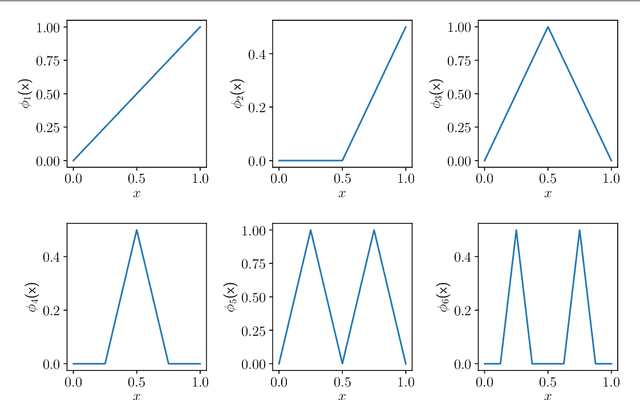
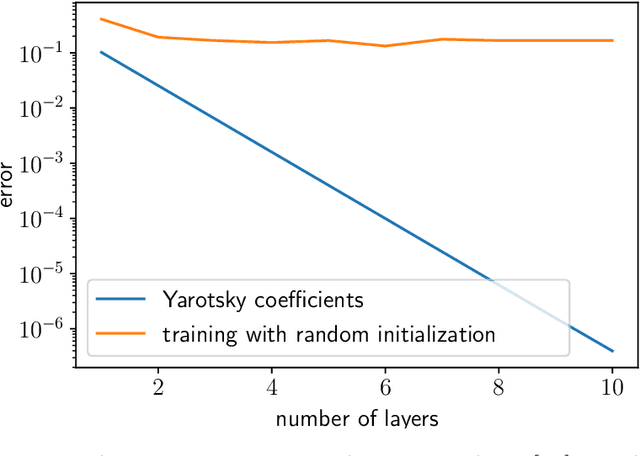
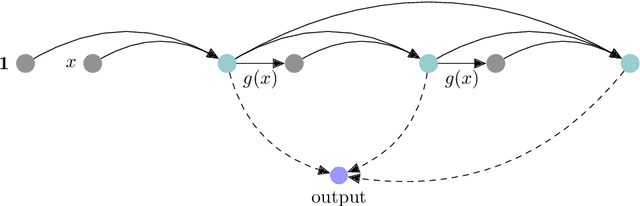
We propose a new method for learning deep neural network models that is based on a greedy learning approach: we add one basis function at a time, and a new basis function is generated as a non-linear activation function applied to a linear combination of the previous basis functions. Such a method (growing deep neural network by one neuron at a time) allows us to compute much more accurate approximants for several model problems in function approximation.