The Ky Fan Norms and Beyond: Dual Norms and Combinations for Matrix Optimization

In this article, we explore the use of various matrix norms for optimizing functions of weight matrices, a crucial problem in training large language models. Moving beyond the spectral norm underlying the Muon update, we leverage duals of the Ky Fan $k$-norms to introduce a family of Muon-like algorithms we name Fanions, which are closely related to Dion. By working with duals of convex combinations of the Ky Fan $k$-norms with either the Frobenius norm or the $l_\infty$ norm, we construct the families of F-Fanions and S-Fanions, respectively. Their most prominent members are F-Muon and S-Muon. We complement our theoretical analysis with an extensive empirical study of these algorithms across a wide range of tasks and settings, demonstrating that F-Muon and S-Muon consistently match Muon's performance, while outperforming vanilla Muon on a synthetic linear least squares problem.

Quantization of Large Language Models with an Overdetermined Basis

In this paper, we introduce an algorithm for data quantization based on the principles of Kashin representation. This approach hinges on decomposing any given vector, matrix, or tensor into two factors. The first factor maintains a small infinity norm, while the second exhibits a similarly constrained norm when multiplied by an orthogonal matrix. Surprisingly, the entries of factors after decomposition are well-concentrated around several peaks, which allows us to efficiently replace them with corresponding centroids for quantization purposes. We study the theoretical properties of the proposed approach and rigorously evaluate our compression algorithm in the context of next-word prediction tasks and on a set of downstream tasks for text classification. Our findings demonstrate that Kashin Quantization achieves competitive or superior quality in model performance while ensuring data compression, marking a significant advancement in the field of data quantization.

NAG-GS: Semi-Implicit, Accelerated and Robust Stochastic Optimizers

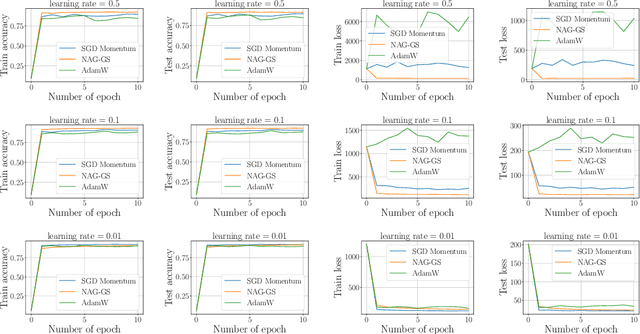
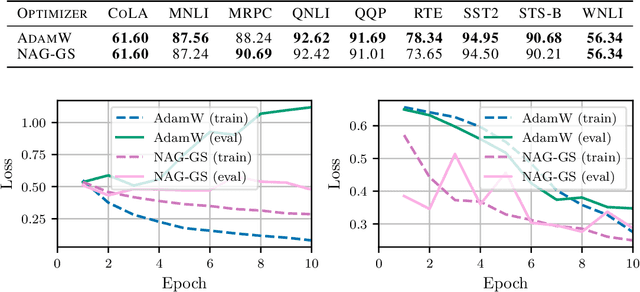
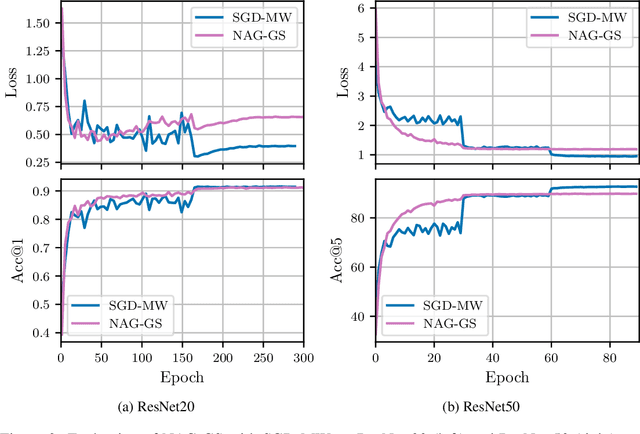
Classical machine learning models such as deep neural networks are usually trained by using Stochastic Gradient Descent-based (SGD) algorithms. The classical SGD can be interpreted as a discretization of the stochastic gradient flow. In this paper we propose a novel, robust and accelerated stochastic optimizer that relies on two key elements: (1) an accelerated Nesterov-like Stochastic Differential Equation (SDE) and (2) its semi-implicit Gauss-Seidel type discretization. The convergence and stability of the obtained method, referred to as NAG-GS, are first studied extensively in the case of the minimization of a quadratic function. This analysis allows us to come up with an optimal step size (or learning rate) in terms of rate of convergence while ensuring the stability of NAG-GS. This is achieved by the careful analysis of the spectral radius of the iteration matrix and the covariance matrix at stationarity with respect to all hyperparameters of our method. We show that NAG-GS is competitive with state-of-the-art methods such as momentum SGD with weight decay and AdamW for the training of machine learning models such as the logistic regression model, the residual networks models on standard computer vision datasets, and Transformers in the frame of the GLUE benchmark.

Memory-Efficient Backpropagation through Large Linear Layers

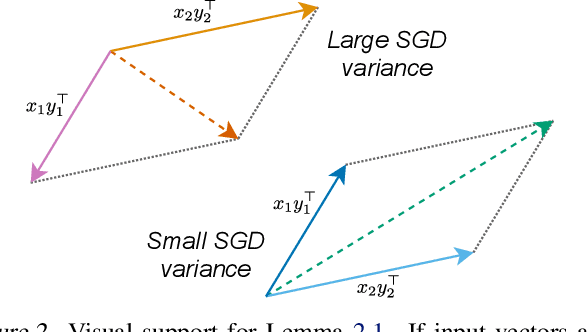
In modern neural networks like Transformers, linear layers require significant memory to store activations during backward pass. This study proposes a memory reduction approach to perform backpropagation through linear layers. Since the gradients of linear layers are computed by matrix multiplications, we consider methods for randomized matrix multiplications and demonstrate that they require less memory with a moderate decrease of the test accuracy. Also, we investigate the variance of the gradient estimate induced by the randomized matrix multiplication. We compare this variance with the variance coming from gradient estimation based on the batch of samples. We demonstrate the benefits of the proposed method on the fine-tuning of the pre-trained RoBERTa model on GLUE tasks.

Fast Line Search for Multi-Task Learning

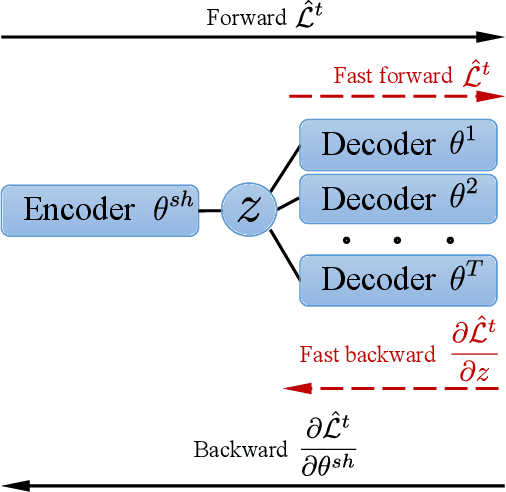
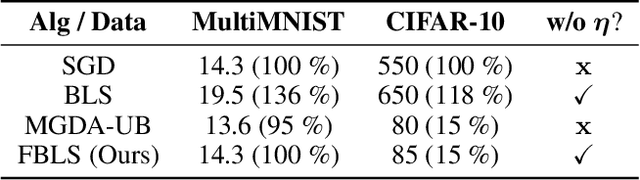
Multi-task learning is a powerful method for solving several tasks jointly by learning robust representation. Optimization of the multi-task learning model is a more complex task than a single-task due to task conflict. Based on theoretical results, convergence to the optimal point is guaranteed when step size is chosen through line search. But, usually, line search for the step size is not the best choice due to the large computational time overhead. We propose a novel idea for line search algorithms in multi-task learning. The idea is to use latent representation space instead of parameter space for finding step size. We examined this idea with backtracking line search. We compare this fast backtracking algorithm with classical backtracking and gradient methods with a constant learning rate on MNIST, CIFAR-10, Cityscapes tasks. The systematic empirical study showed that the proposed method leads to more accurate and fast solution, than the traditional backtracking approach and keep competitive computational time and performance compared to the constant learning rate method.

Follow the bisector: a simple method for multi-objective optimization

This study presents a novel Equiangular Direction Method (EDM) to solve a multi-objective optimization problem. We consider optimization problems, where multiple differentiable losses have to be minimized. The presented method computes descent direction in every iteration to guarantee equal relative decrease of objective functions. This descent direction is based on the normalized gradients of the individual losses. Therefore, it is appropriate to solve multi-objective optimization problems with multi-scale losses. We test the proposed method on the imbalanced classification problem and multi-task learning problem, where standard datasets are used. EDM is compared with other methods to solve these problems.

Stochastic gradient algorithms from ODE splitting perspective

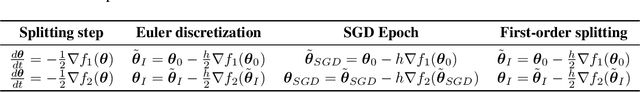
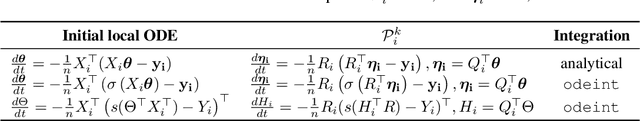
We present a different view on stochastic optimization, which goes back to the splitting schemes for approximate solutions of ODE. In this work, we provide a connection between stochastic gradient descent approach and first-order splitting scheme for ODE. We consider the special case of splitting, which is inspired by machine learning applications and derive a new upper bound on the global splitting error for it. We present, that the Kaczmarz method is the limit case of the splitting scheme for the unit batch SGD for linear least squares problem. We support our findings with systematic empirical studies, which demonstrates, that a more accurate solution of local problems leads to the stepsize robustness and provides better convergence in time and iterations on the softmax regression problem.

Empirical study of extreme overfitting points of neural networks

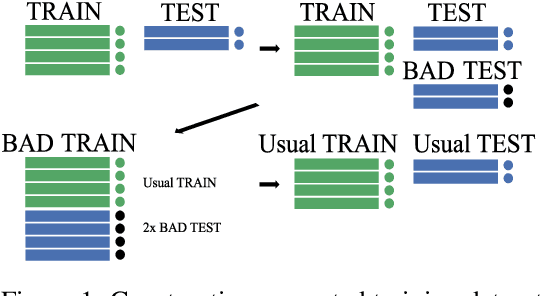
In this paper we propose a method of obtaining points of extreme overfitting - parameters of modern neural networks, at which they demonstrate close to 100 % training accuracy, simultaneously with almost zero accuracy on the test sample. Despite the widespread opinion that the overwhelming majority of critical points of the loss function of a neural network have equally good generalizing ability, such points have a huge generalization error. The paper studies the properties of such points and their location on the surface of the loss function of modern neural networks.