Quantization Aware Factorization for Deep Neural Network Compression

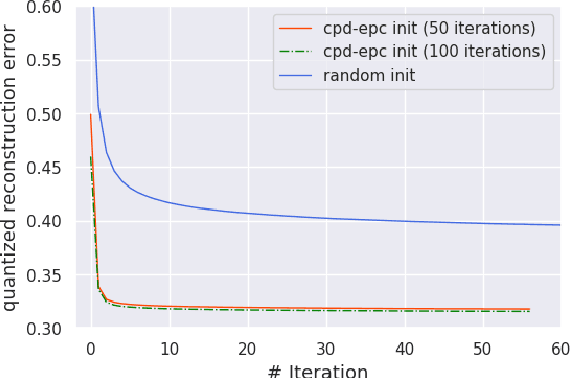
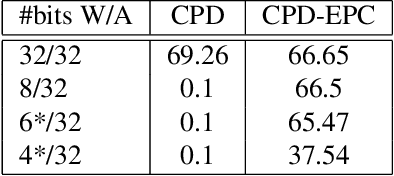
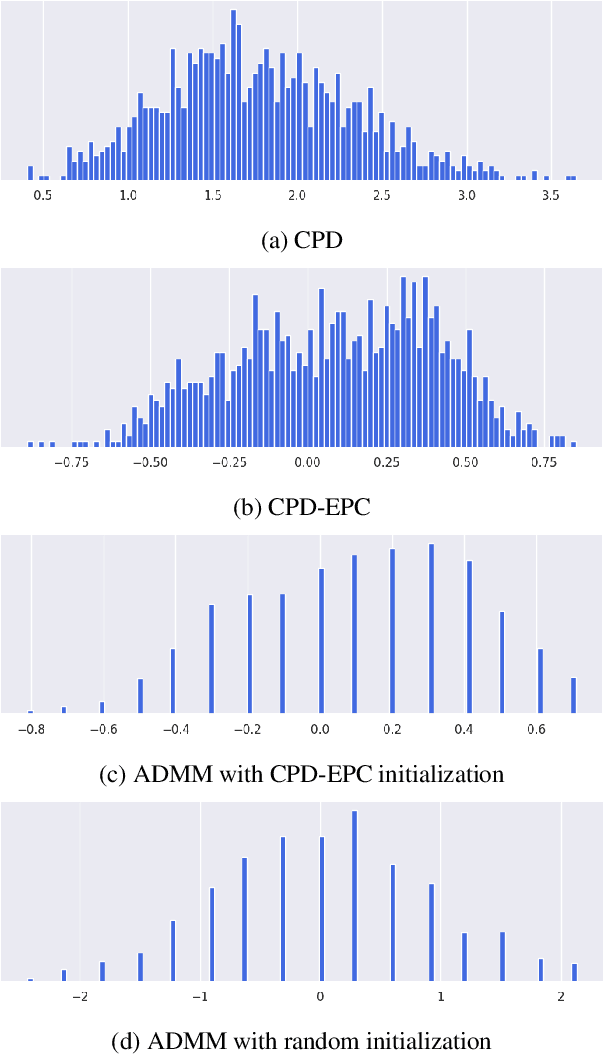
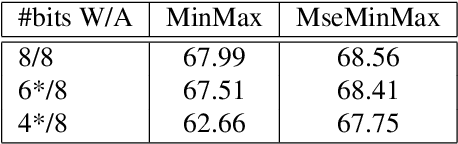
Tensor decomposition of convolutional and fully-connected layers is an effective way to reduce parameters and FLOP in neural networks. Due to memory and power consumption limitations of mobile or embedded devices, the quantization step is usually necessary when pre-trained models are deployed. A conventional post-training quantization approach applied to networks with decomposed weights yields a drop in accuracy. This motivated us to develop an algorithm that finds tensor approximation directly with quantized factors and thus benefit from both compression techniques while keeping the prediction quality of the model. Namely, we propose to use Alternating Direction Method of Multipliers (ADMM) for Canonical Polyadic (CP) decomposition with factors whose elements lie on a specified quantization grid. We compress neural network weights with a devised algorithm and evaluate it's prediction quality and performance. We compare our approach to state-of-the-art post-training quantization methods and demonstrate competitive results and high flexibility in achiving a desirable quality-performance tradeoff.

Rockmate: an Efficient, Fast, Automatic and Generic Tool for Re-materialization in PyTorch

We propose Rockmate to control the memory requirements when training PyTorch DNN models. Rockmate is an automatic tool that starts from the model code and generates an equivalent model, using a predefined amount of memory for activations, at the cost of a few re-computations. Rockmate automatically detects the structure of computational and data dependencies and rewrites the initial model as a sequence of complex blocks. We show that such a structure is widespread and can be found in many models in the literature (Transformer based models, ResNet, RegNets,...). This structure allows us to solve the problem in a fast and efficient way, using an adaptation of Checkmate (too slow on the whole model but general) at the level of individual blocks and an adaptation of Rotor (fast but limited to sequential models) at the level of the sequence itself. We show through experiments on many models that Rockmate is as fast as Rotor and as efficient as Checkmate, and that it allows in many cases to obtain a significantly lower memory consumption for activations (by a factor of 2 to 5) for a rather negligible overhead (of the order of 10% to 20%). Rockmate is open source and available at https://github.com/topal-team/rockmate.

Efficient GPT Model Pre-training using Tensor Train Matrix Representation

Large-scale transformer models have shown remarkable performance in language modelling tasks. However, such models feature billions of parameters, leading to difficulties in their deployment and prohibitive training costs from scratch. To reduce the number of the parameters in the GPT-2 architecture, we replace the matrices of fully-connected layers with the corresponding Tensor Train Matrix~(TTM) structure. Finally, we customize forward and backward operations through the TTM-based layer for simplicity and the stableness of further training. % The resulting GPT-2-based model stores up to 40% fewer parameters, showing the perplexity comparable to the original model. On the downstream tasks, including language understanding and text summarization, the model performs similarly to the original GPT-2 model. The proposed tensorized layers could be used to efficiently pre-training other Transformer models.

Survey on Large Scale Neural Network Training

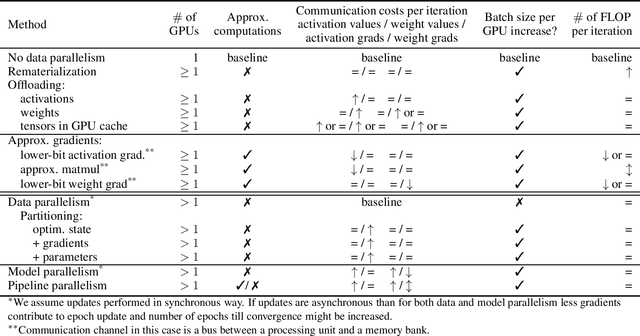
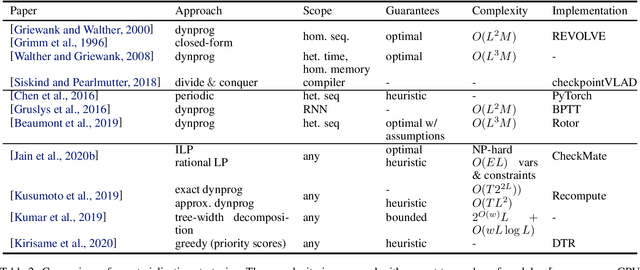
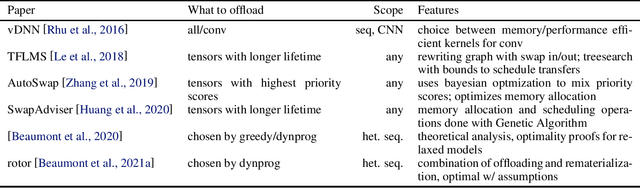
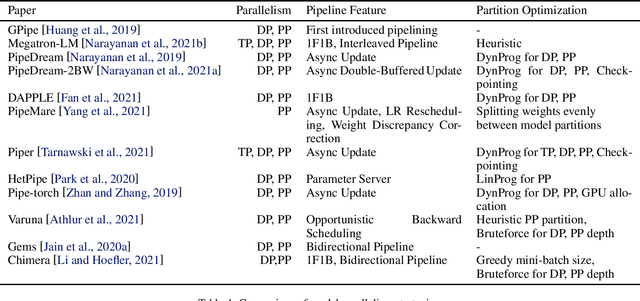
Modern Deep Neural Networks (DNNs) require significant memory to store weight, activations, and other intermediate tensors during training. Hence, many models do not fit one GPU device or can be trained using only a small per-GPU batch size. This survey provides a systematic overview of the approaches that enable more efficient DNNs training. We analyze techniques that save memory and make good use of computation and communication resources on architectures with a single or several GPUs. We summarize the main categories of strategies and compare strategies within and across categories. Along with approaches proposed in the literature, we discuss available implementations.

Memory-Efficient Backpropagation through Large Linear Layers

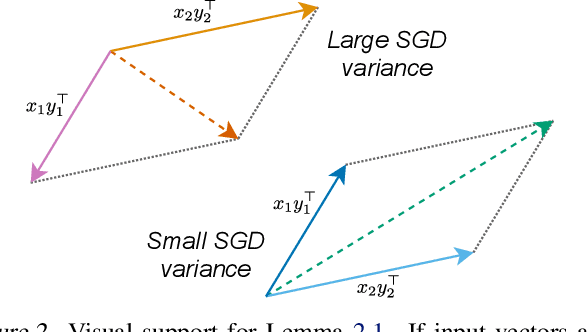
In modern neural networks like Transformers, linear layers require significant memory to store activations during backward pass. This study proposes a memory reduction approach to perform backpropagation through linear layers. Since the gradients of linear layers are computed by matrix multiplications, we consider methods for randomized matrix multiplications and demonstrate that they require less memory with a moderate decrease of the test accuracy. Also, we investigate the variance of the gradient estimate induced by the randomized matrix multiplication. We compare this variance with the variance coming from gradient estimation based on the batch of samples. We demonstrate the benefits of the proposed method on the fine-tuning of the pre-trained RoBERTa model on GLUE tasks.

Few-Bit Backward: Quantized Gradients of Activation Functions for Memory Footprint Reduction

Memory footprint is one of the main limiting factors for large neural network training. In backpropagation, one needs to store the input to each operation in the computational graph. Every modern neural network model has quite a few pointwise nonlinearities in its architecture, and such operation induces additional memory costs which -- as we show -- can be significantly reduced by quantization of the gradients. We propose a systematic approach to compute optimal quantization of the retained gradients of the pointwise nonlinear functions with only a few bits per each element. We show that such approximation can be achieved by computing optimal piecewise-constant approximation of the derivative of the activation function, which can be done by dynamic programming. The drop-in replacements are implemented for all popular nonlinearities and can be used in any existing pipeline. We confirm the memory reduction and the same convergence on several open benchmarks.

Meta-Solver for Neural Ordinary Differential Equations

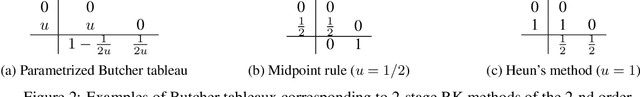
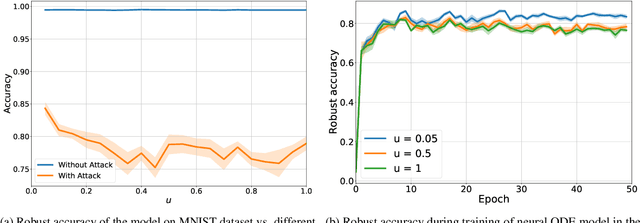
A conventional approach to train neural ordinary differential equations (ODEs) is to fix an ODE solver and then learn the neural network's weights to optimize a target loss function. However, such an approach is tailored for a specific discretization method and its properties, which may not be optimal for the selected application and yield the overfitting to the given solver. In our paper, we investigate how the variability in solvers' space can improve neural ODEs performance. We consider a family of Runge-Kutta methods that are parameterized by no more than two scalar variables. Based on the solvers' properties, we propose an approach to decrease neural ODEs overfitting to the pre-defined solver, along with a criterion to evaluate such behaviour. Moreover, we show that the right choice of solver parameterization can significantly affect neural ODEs models in terms of robustness to adversarial attacks. Recently it was shown that neural ODEs demonstrate superiority over conventional CNNs in terms of robustness. Our work demonstrates that the model robustness can be further improved by optimizing solver choice for a given task. The source code to reproduce our experiments is available at https://github.com/juliagusak/neural-ode-metasolver.

Stable Low-rank Tensor Decomposition for Compression of Convolutional Neural Network

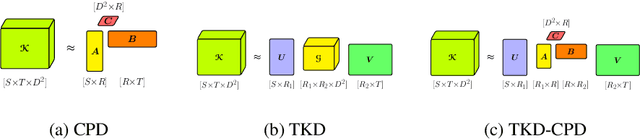
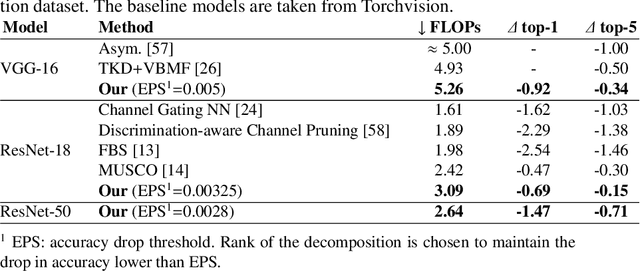
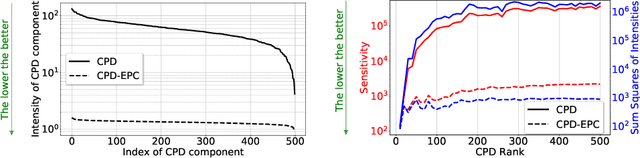
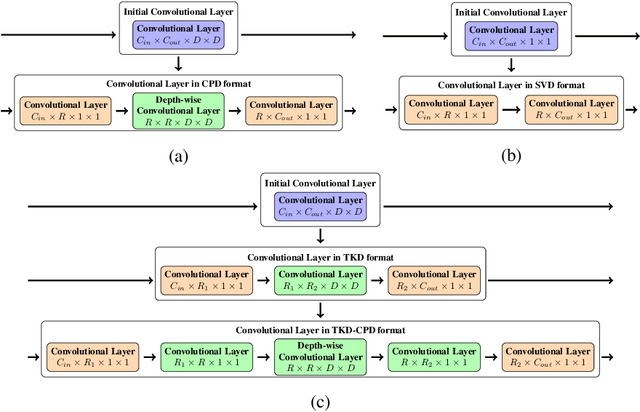
Most state of the art deep neural networks are overparameterized and exhibit a high computational cost. A straightforward approach to this problem is to replace convolutional kernels with its low-rank tensor approximations, whereas the Canonical Polyadic tensor Decomposition is one of the most suited models. However, fitting the convolutional tensors by numerical optimization algorithms often encounters diverging components, i.e., extremely large rank-one tensors but canceling each other. Such degeneracy often causes the non-interpretable result and numerical instability for the neural network fine-tuning. This paper is the first study on degeneracy in the tensor decomposition of convolutional kernels. We present a novel method, which can stabilize the low-rank approximation of convolutional kernels and ensure efficient compression while preserving the high-quality performance of the neural networks. We evaluate our approach on popular CNN architectures for image classification and show that our method results in much lower accuracy degradation and provides consistent performance.

Towards Understanding Normalization in Neural ODEs

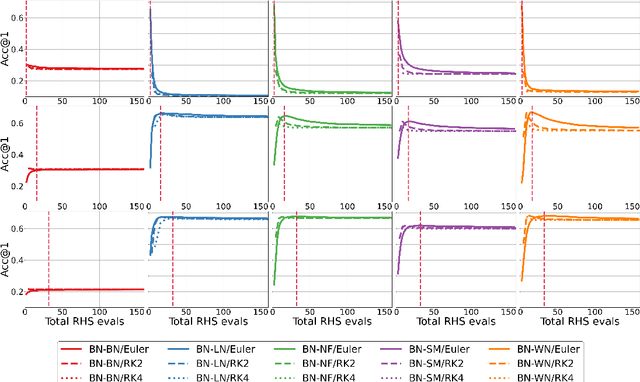
Normalization is an important and vastly investigated technique in deep learning. However, its role for Ordinary Differential Equation based networks (neural ODEs) is still poorly understood. This paper investigates how different normalization techniques affect the performance of neural ODEs. Particularly, we show that it is possible to achieve 93% accuracy in the CIFAR-10 classification task, and to the best of our knowledge, this is the highest reported accuracy among neural ODEs tested on this problem.

Interpolated Adjoint Method for Neural ODEs

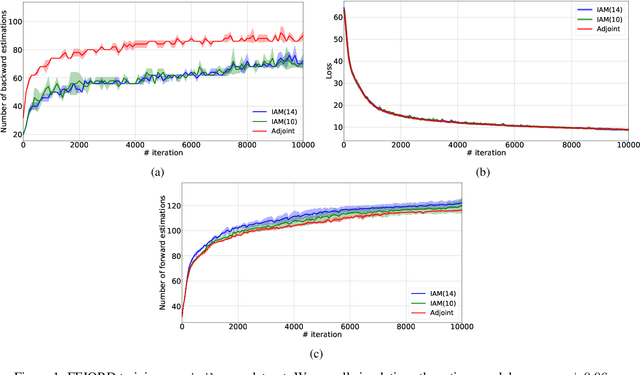
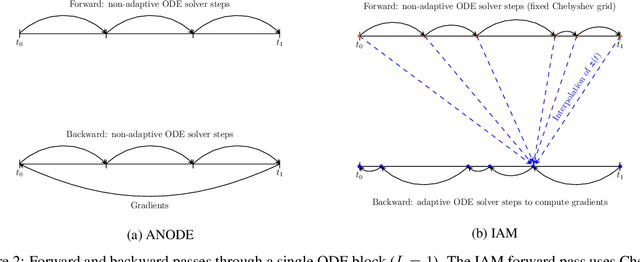
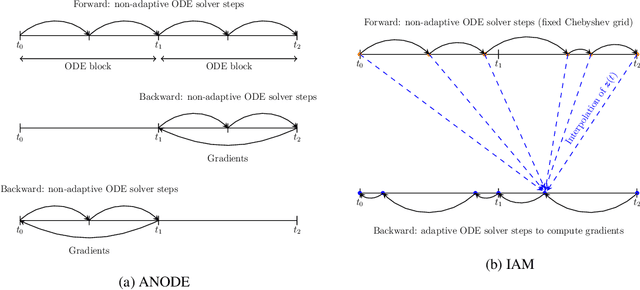
In this paper, we propose a method, which allows us to alleviate or completely avoid the notorious problem of numerical instability and stiffness of the adjoint method for training neural ODE. On the backward pass, we propose to use the machinery of smooth function interpolation to restore the trajectory obtained during the forward integration. We show the viability of our approach, both in theory and practice.