Andrzej Cichocki
Spontaneous Spatial Cognition Emerges during Egocentric Video Viewing through Non-invasive BCI
Jul 16, 2025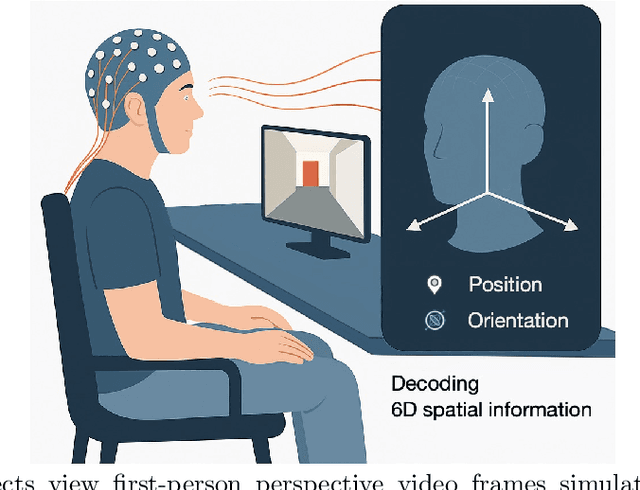


Abstract:Humans possess a remarkable capacity for spatial cognition, allowing for self-localization even in novel or unfamiliar environments. While hippocampal neurons encoding position and orientation are well documented, the large-scale neural dynamics supporting spatial representation, particularly during naturalistic, passive experience, remain poorly understood. Here, we demonstrate for the first time that non-invasive brain-computer interfaces (BCIs) based on electroencephalography (EEG) can decode spontaneous, fine-grained egocentric 6D pose, comprising three-dimensional position and orientation, during passive viewing of egocentric video. Despite EEG's limited spatial resolution and high signal noise, we find that spatially coherent visual input (i.e., continuous and structured motion) reliably evokes decodable spatial representations, aligning with participants' subjective sense of spatial engagement. Decoding performance further improves when visual input is presented at a frame rate of 100 ms per image, suggesting alignment with intrinsic neural temporal dynamics. Using gradient-based backpropagation through a neural decoding model, we identify distinct EEG channels contributing to position -- and orientation specific -- components, revealing a distributed yet complementary neural encoding scheme. These findings indicate that the brain's spatial systems operate spontaneously and continuously, even under passive conditions, challenging traditional distinctions between active and passive spatial cognition. Our results offer a non-invasive window into the automatic construction of egocentric spatial maps and advance our understanding of how the human mind transforms everyday sensory experience into structured internal representations.
Mirror Descent and Novel Exponentiated Gradient Algorithms Using Trace-Form Entropies and Deformed Logarithms
Mar 11, 2025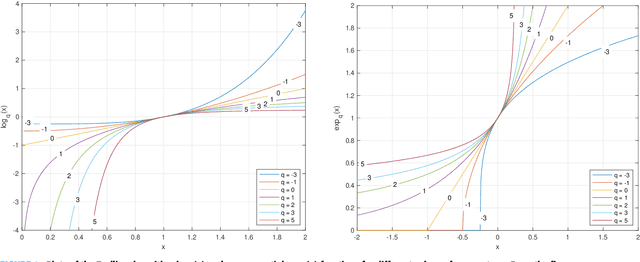
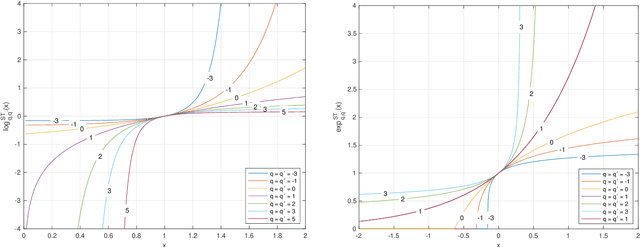
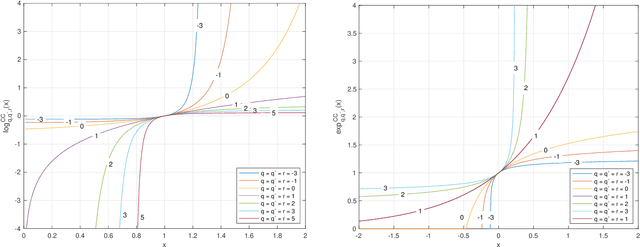
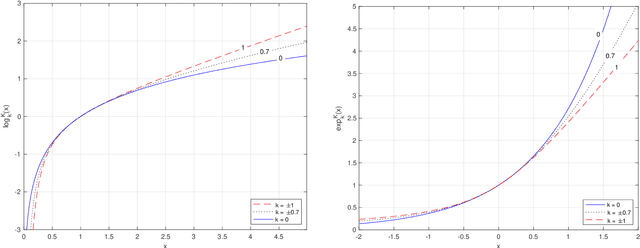
Abstract:In this paper we propose and investigate a wide class of Mirror Descent updates (MD) and associated novel Generalized Exponentiated Gradient (GEG) algorithms by exploiting various trace-form entropies and associated deformed logarithms and their inverses - deformed (generalized) exponential functions. The proposed algorithms can be considered as extension of entropic MD and generalization of multiplicative updates. In the literature, there exist nowadays over fifty mathematically well defined generalized entropies, so impossible to exploit all of them in one research paper. So we focus on a few selected most popular entropies and associated logarithms like the Tsallis, Kaniadakis and Sharma-Taneja-Mittal and some of their extension like Tempesta or Kaniadakis-Scarfone entropies. The shape and properties of the deformed logarithms and their inverses are tuned by one or more hyperparameters. By learning these hyperparameters, we can adapt to distribution of training data, which can be designed to the specific geometry of the optimization problem, leading to potentially faster convergence and better performance. The using generalized entropies and associated deformed logarithms in the Bregman divergence, used as a regularization term, provides some new insight into exponentiated gradient descent updates.
VQ-Flow: Taming Normalizing Flows for Multi-Class Anomaly Detection via Hierarchical Vector Quantization
Sep 02, 2024
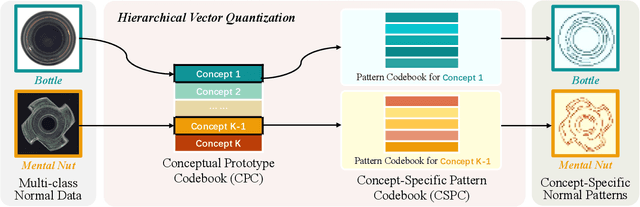
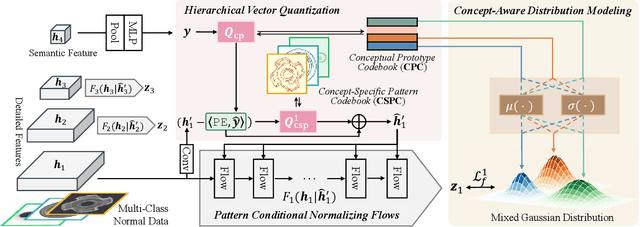
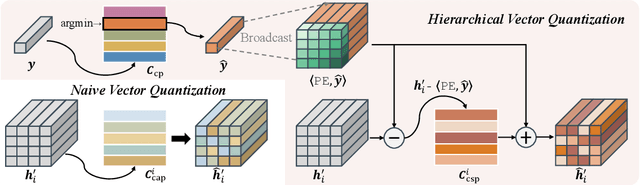
Abstract:Normalizing flows, a category of probabilistic models famed for their capabilities in modeling complex data distributions, have exhibited remarkable efficacy in unsupervised anomaly detection. This paper explores the potential of normalizing flows in multi-class anomaly detection, wherein the normal data is compounded with multiple classes without providing class labels. Through the integration of vector quantization (VQ), we empower the flow models to distinguish different concepts of multi-class normal data in an unsupervised manner, resulting in a novel flow-based unified method, named VQ-Flow. Specifically, our VQ-Flow leverages hierarchical vector quantization to estimate two relative codebooks: a Conceptual Prototype Codebook (CPC) for concept distinction and its concomitant Concept-Specific Pattern Codebook (CSPC) to capture concept-specific normal patterns. The flow models in VQ-Flow are conditioned on the concept-specific patterns captured in CSPC, capable of modeling specific normal patterns associated with different concepts. Moreover, CPC further enables our VQ-Flow for concept-aware distribution modeling, faithfully mimicking the intricate multi-class normal distribution through a mixed Gaussian distribution reparametrized on the conceptual prototypes. Through the introduction of vector quantization, the proposed VQ-Flow advances the state-of-the-art in multi-class anomaly detection within a unified training scheme, yielding the Det./Loc. AUROC of 99.5%/98.3% on MVTec AD. The codebase is publicly available at https://github.com/cool-xuan/vqflow.
Generalized Exponentiated Gradient Algorithms and Their Application to On-Line Portfolio Selection
Jun 02, 2024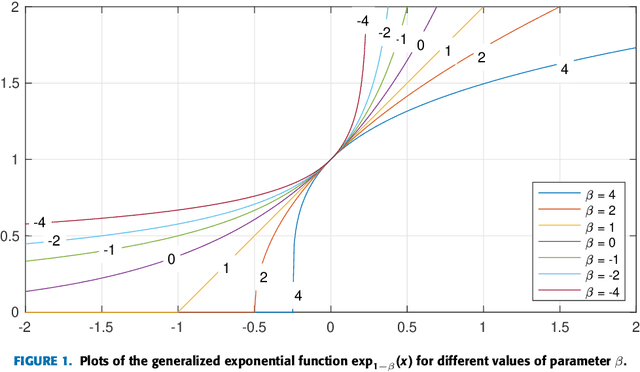
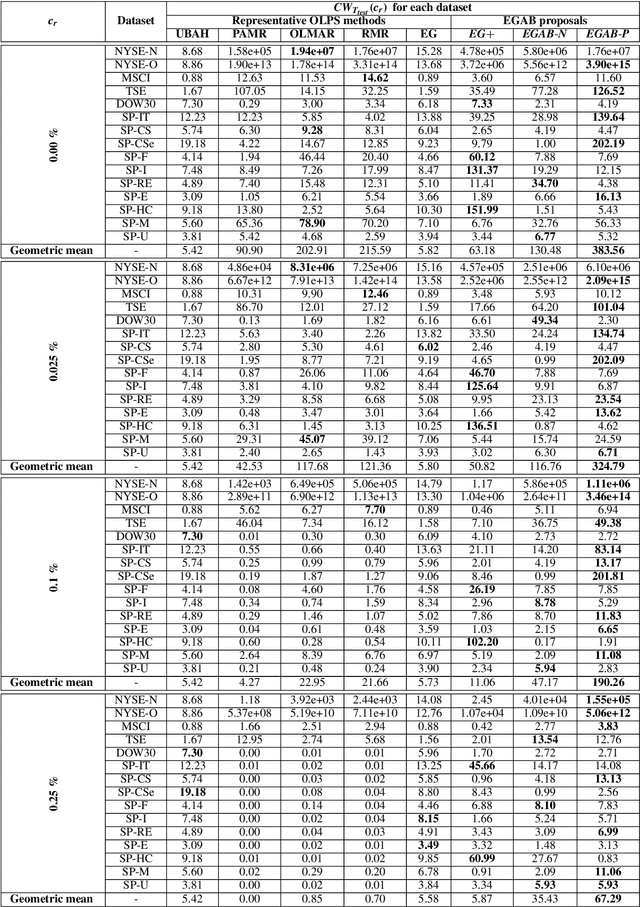
Abstract:This paper introduces a novel family of generalized exponentiated gradient (EG) updates derived from an Alpha-Beta divergence regularization function. Collectively referred to as EGAB, the proposed updates belong to the category of multiplicative gradient algorithms for positive data and demonstrate considerable flexibility by controlling iteration behavior and performance through three hyperparameters: $\alpha$, $\beta$, and the learning rate $\eta$. To enforce a unit $l_1$ norm constraint for nonnegative weight vectors within generalized EGAB algorithms, we develop two slightly distinct approaches. One method exploits scale-invariant loss functions, while the other relies on gradient projections onto the feasible domain. As an illustration of their applicability, we evaluate the proposed updates in addressing the online portfolio selection problem (OLPS) using gradient-based methods. Here, they not only offer a unified perspective on the search directions of various OLPS algorithms (including the standard exponentiated gradient and diverse mean-reversion strategies), but also facilitate smooth interpolation and extension of these updates due to the flexibility in hyperparameter selection. Simulation results confirm that the adaptability of these generalized gradient updates can effectively enhance the performance for some portfolios, particularly in scenarios involving transaction costs.
Quantization Aware Factorization for Deep Neural Network Compression
Aug 08, 2023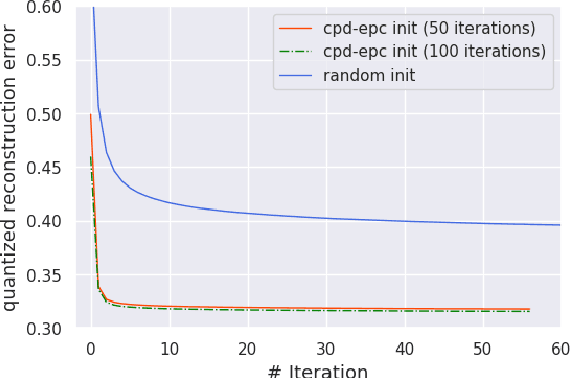
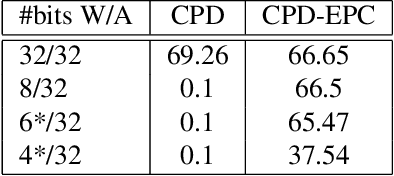
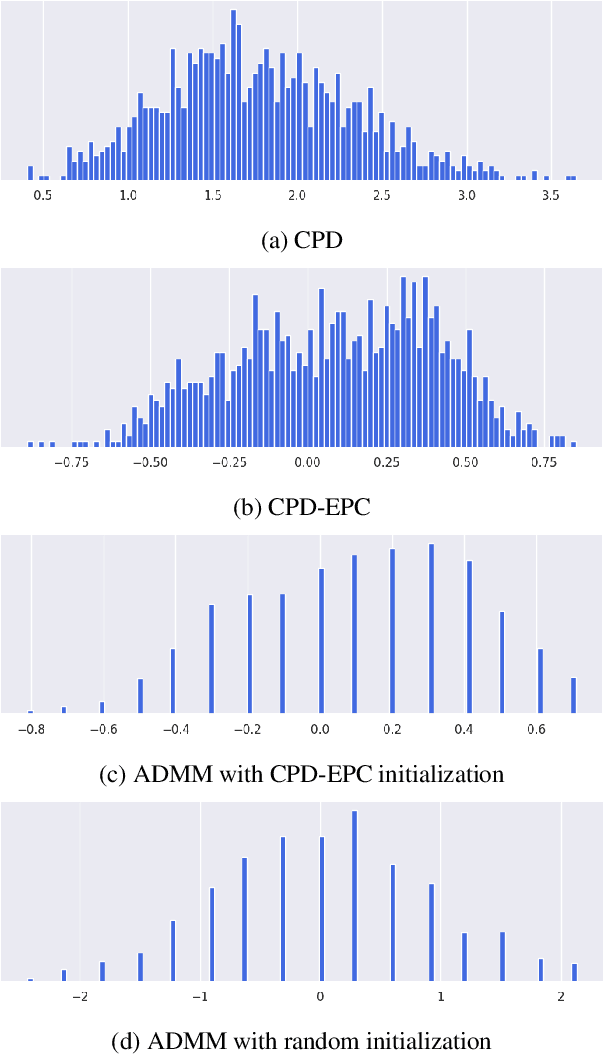
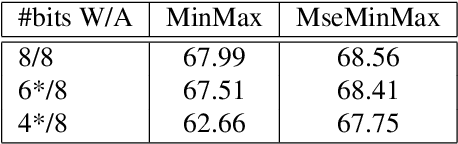
Abstract:Tensor decomposition of convolutional and fully-connected layers is an effective way to reduce parameters and FLOP in neural networks. Due to memory and power consumption limitations of mobile or embedded devices, the quantization step is usually necessary when pre-trained models are deployed. A conventional post-training quantization approach applied to networks with decomposed weights yields a drop in accuracy. This motivated us to develop an algorithm that finds tensor approximation directly with quantized factors and thus benefit from both compression techniques while keeping the prediction quality of the model. Namely, we propose to use Alternating Direction Method of Multipliers (ADMM) for Canonical Polyadic (CP) decomposition with factors whose elements lie on a specified quantization grid. We compress neural network weights with a devised algorithm and evaluate it's prediction quality and performance. We compare our approach to state-of-the-art post-training quantization methods and demonstrate competitive results and high flexibility in achiving a desirable quality-performance tradeoff.
Optical Coherence Tomography Image Enhancement via Block Hankelization and Low Rank Tensor Network Approximation
Jun 19, 2023Abstract:In this paper, the problem of image super-resolution for Optical Coherence Tomography (OCT) has been addressed. Due to the motion artifacts, OCT imaging is usually done with a low sampling rate and the resulting images are often noisy and have low resolution. Therefore, reconstruction of high resolution OCT images from the low resolution versions is an essential step for better OCT based diagnosis. In this paper, we propose a novel OCT super-resolution technique using Tensor Ring decomposition in the embedded space. A new tensorization method based on a block Hankelization approach with overlapped patches, called overlapped patch Hankelization, has been proposed which allows us to employ Tensor Ring decomposition. The Hankelization method enables us to better exploit the inter connection of pixels and consequently achieve better super-resolution of images. The low resolution image was first patch Hankelized and then its Tensor Ring decomposition with rank incremental has been computed. Simulation results confirm that the proposed approach is effective in OCT super-resolution.
Lightweight Attribute Localizing Models for Pedestrian Attribute Recognition
Jun 16, 2023
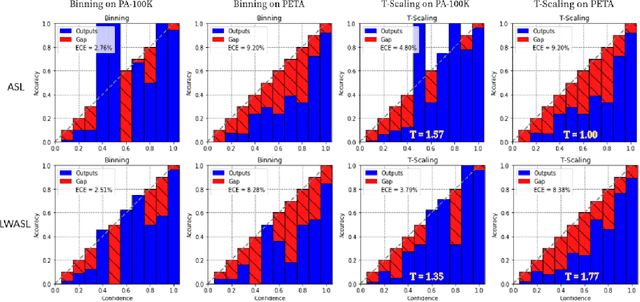
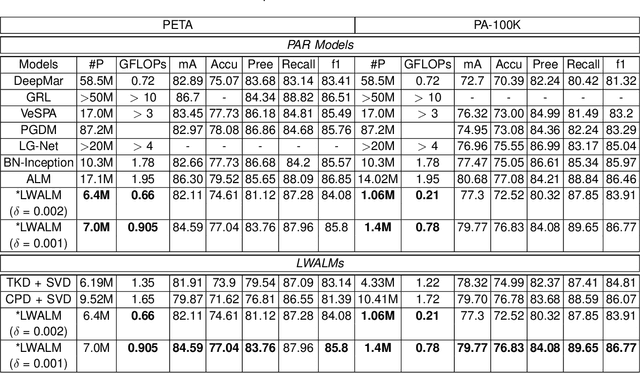
Abstract:Pedestrian Attribute Recognition (PAR) deals with the problem of identifying features in a pedestrian image. It has found interesting applications in person retrieval, suspect re-identification and soft biometrics. In the past few years, several Deep Neural Networks (DNNs) have been designed to solve the task; however, the developed DNNs predominantly suffer from over-parameterization and high computational complexity. These problems hinder them from being exploited in resource-constrained embedded devices with limited memory and computational capacity. By reducing a network's layers using effective compression techniques, such as tensor decomposition, neural network compression is an effective method to tackle these problems. We propose novel Lightweight Attribute Localizing Models (LWALM) for Pedestrian Attribute Recognition (PAR). LWALM is a compressed neural network obtained after effective layer-wise compression of the Attribute Localization Model (ALM) using the Canonical Polyadic Decomposition with Error Preserving Correction (CPD-EPC) algorithm.
Image Reconstruction using Superpixel Clustering and Tensor Completion
May 16, 2023Abstract:This paper presents a pixel selection method for compact image representation based on superpixel segmentation and tensor completion. Our method divides the image into several regions that capture important textures or semantics and selects a representative pixel from each region to store. We experiment with different criteria for choosing the representative pixel and find that the centroid pixel performs the best. We also propose two smooth tensor completion algorithms that can effectively reconstruct different types of images from the selected pixels. Our experiments show that our superpixel-based method achieves better results than uniform sampling for various missing ratios.
TTOpt: A Maximum Volume Quantized Tensor Train-based Optimization and its Application to Reinforcement Learning
Apr 30, 2022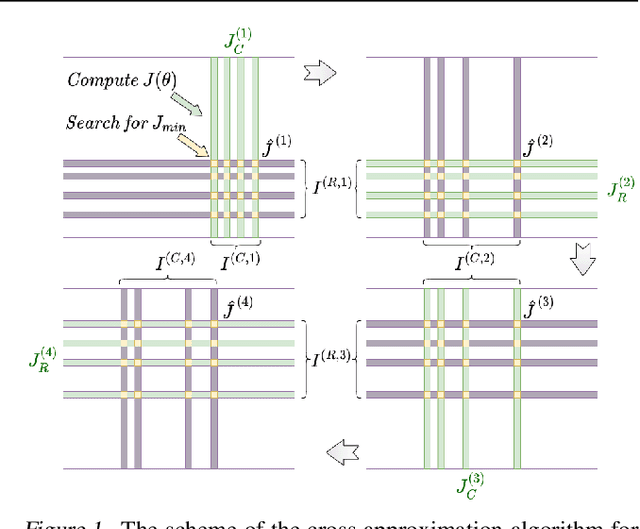
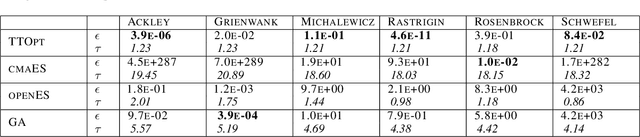
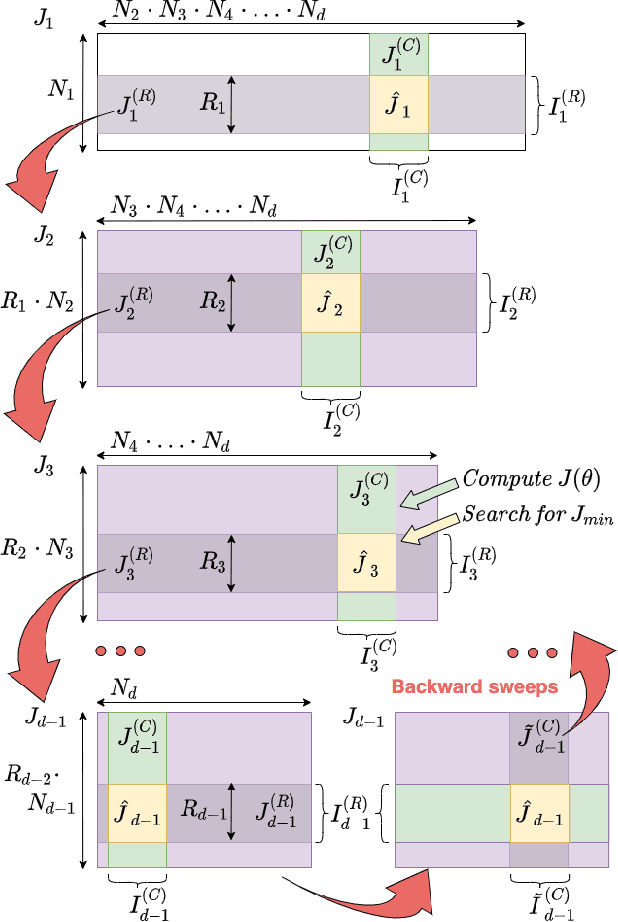
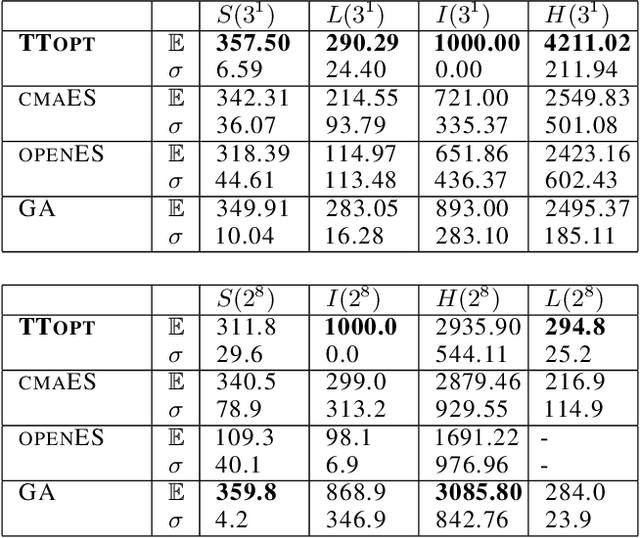
Abstract:We present a novel procedure for optimization based on the combination of efficient quantized tensor train representation and a generalized maximum matrix volume principle. We demonstrate the applicability of the new Tensor Train Optimizer (TTOpt) method for various tasks, ranging from minimization of multidimensional functions to reinforcement learning. Our algorithm compares favorably to popular evolutionary-based methods and outperforms them by the number of function evaluations or execution time, often by a significant margin.
How to Train Unstable Looped Tensor Network
Mar 05, 2022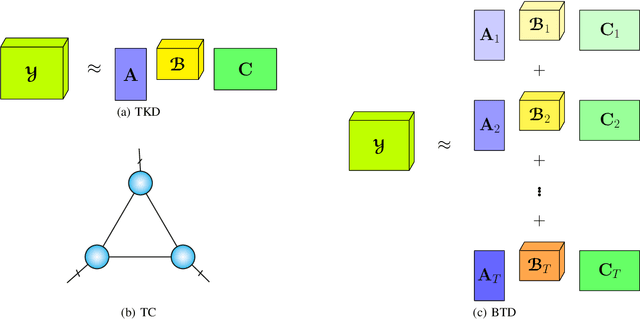
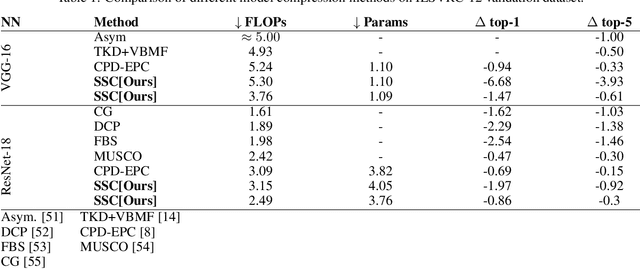
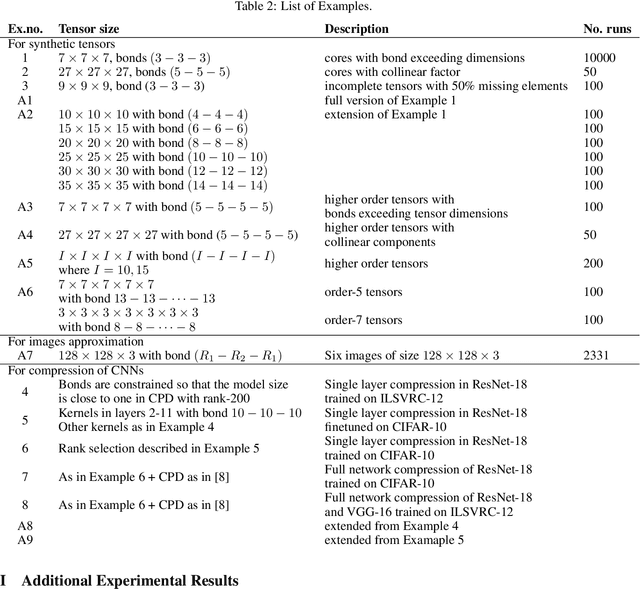
Abstract:A rising problem in the compression of Deep Neural Networks is how to reduce the number of parameters in convolutional kernels and the complexity of these layers by low-rank tensor approximation. Canonical polyadic tensor decomposition (CPD) and Tucker tensor decomposition (TKD) are two solutions to this problem and provide promising results. However, CPD often fails due to degeneracy, making the networks unstable and hard to fine-tune. TKD does not provide much compression if the core tensor is big. This motivates using a hybrid model of CPD and TKD, a decomposition with multiple Tucker models with small core tensor, known as block term decomposition (BTD). This paper proposes a more compact model that further compresses the BTD by enforcing core tensors in BTD identical. We establish a link between the BTD with shared parameters and a looped chain tensor network (TC). Unfortunately, such strongly constrained tensor networks (with loop) encounter severe numerical instability, as proved by y (Landsberg, 2012) and (Handschuh, 2015a). We study perturbation of chain tensor networks, provide interpretation of instability in TC, demonstrate the problem. We propose novel methods to gain the stability of the decomposition results, keep the network robust and attain better approximation. Experimental results will confirm the superiority of the proposed methods in compression of well-known CNNs, and TC decomposition under challenging scenarios
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge