Anh-Huy Phan
TERM Model: Tensor Ring Mixture Model for Density Estimation
Dec 13, 2023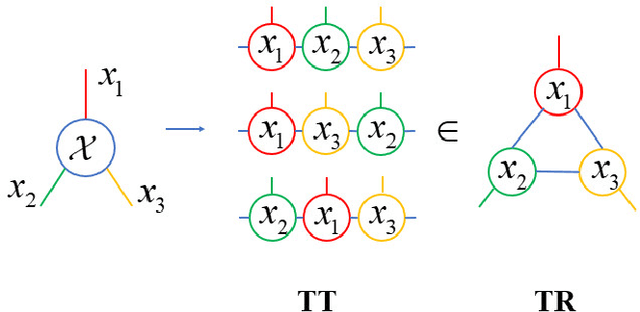
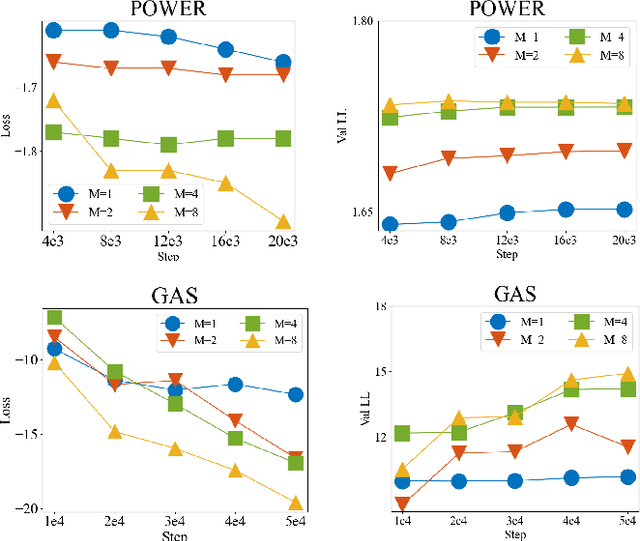
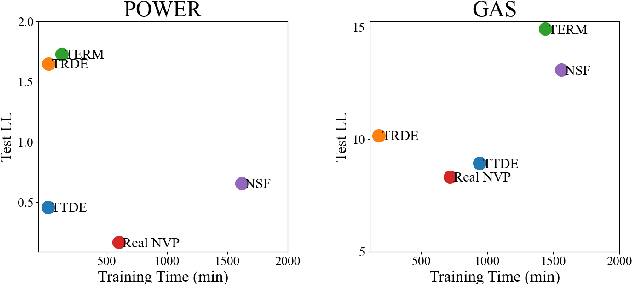
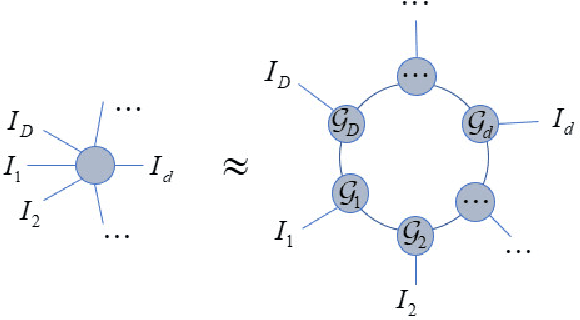
Abstract:Efficient probability density estimation is a core challenge in statistical machine learning. Tensor-based probabilistic graph methods address interpretability and stability concerns encountered in neural network approaches. However, a substantial number of potential tensor permutations can lead to a tensor network with the same structure but varying expressive capabilities. In this paper, we take tensor ring decomposition for density estimator, which significantly reduces the number of permutation candidates while enhancing expressive capability compared with existing used decompositions. Additionally, a mixture model that incorporates multiple permutation candidates with adaptive weights is further designed, resulting in increased expressive flexibility and comprehensiveness. Different from the prevailing directions of tensor network structure/permutation search, our approach provides a new viewpoint inspired by ensemble learning. This approach acknowledges that suboptimal permutations can offer distinctive information besides that of optimal permutations. Experiments show the superiority of the proposed approach in estimating probability density for moderately dimensional datasets and sampling to capture intricate details.
Quantization Aware Factorization for Deep Neural Network Compression
Aug 08, 2023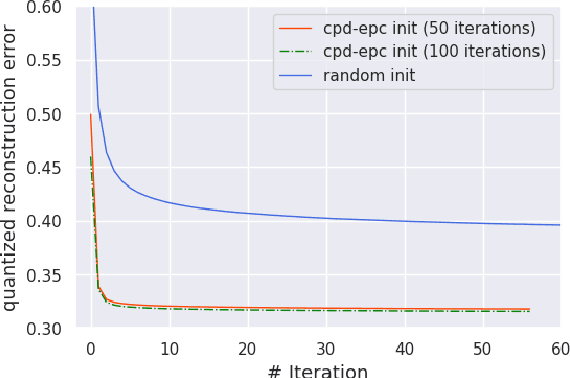
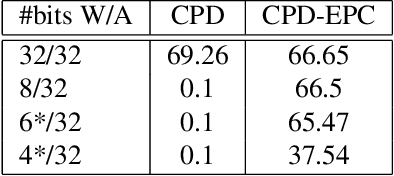
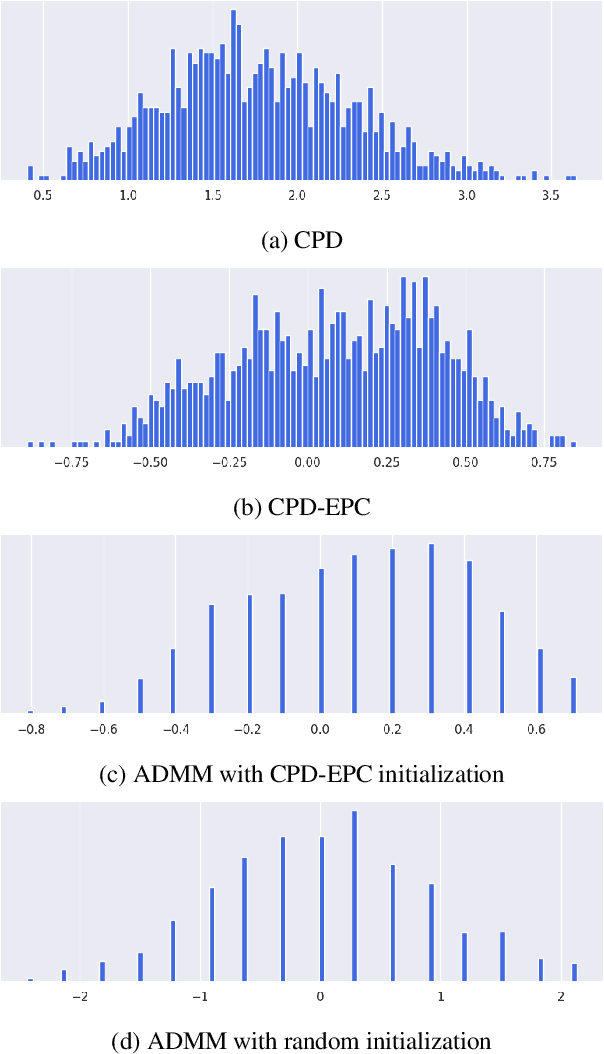
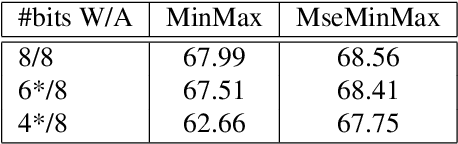
Abstract:Tensor decomposition of convolutional and fully-connected layers is an effective way to reduce parameters and FLOP in neural networks. Due to memory and power consumption limitations of mobile or embedded devices, the quantization step is usually necessary when pre-trained models are deployed. A conventional post-training quantization approach applied to networks with decomposed weights yields a drop in accuracy. This motivated us to develop an algorithm that finds tensor approximation directly with quantized factors and thus benefit from both compression techniques while keeping the prediction quality of the model. Namely, we propose to use Alternating Direction Method of Multipliers (ADMM) for Canonical Polyadic (CP) decomposition with factors whose elements lie on a specified quantization grid. We compress neural network weights with a devised algorithm and evaluate it's prediction quality and performance. We compare our approach to state-of-the-art post-training quantization methods and demonstrate competitive results and high flexibility in achiving a desirable quality-performance tradeoff.
TTOpt: A Maximum Volume Quantized Tensor Train-based Optimization and its Application to Reinforcement Learning
Apr 30, 2022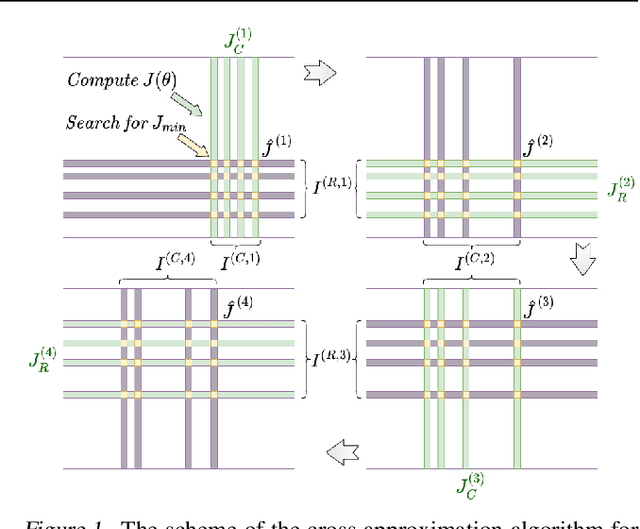
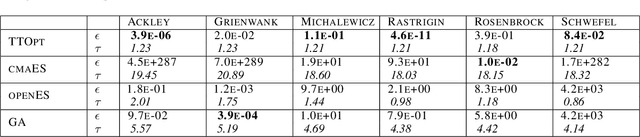
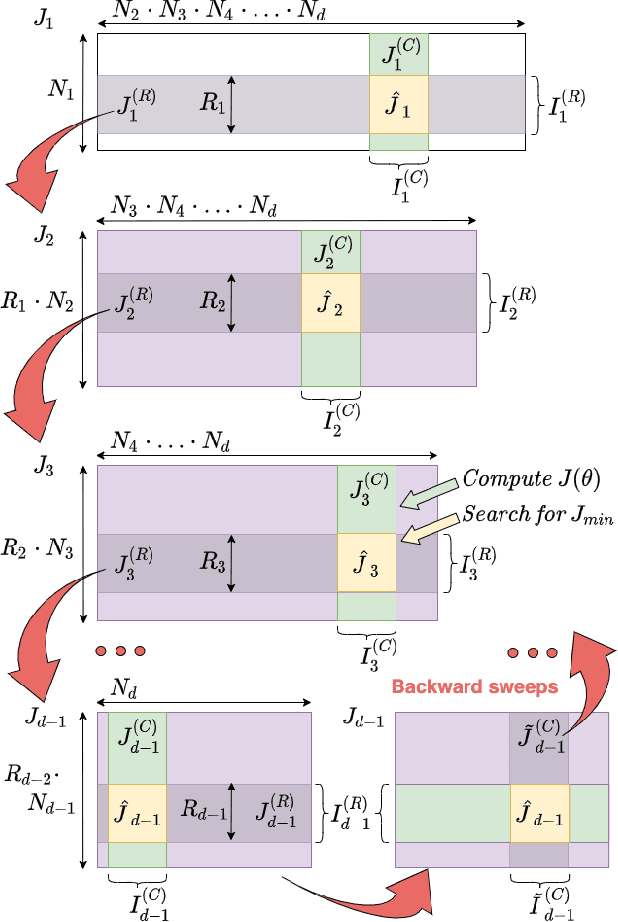
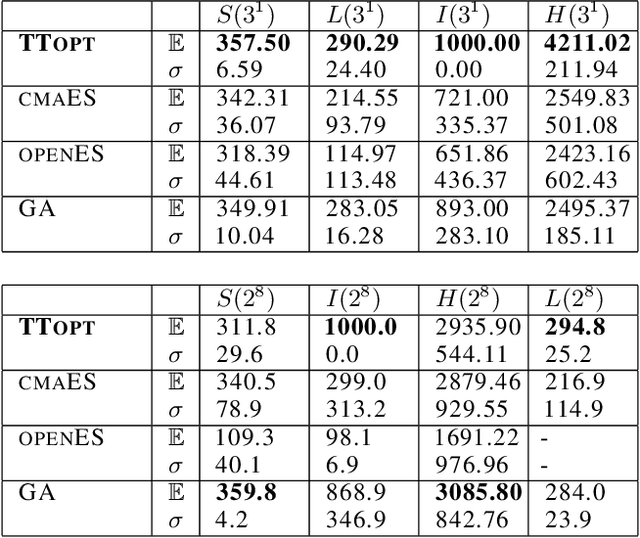
Abstract:We present a novel procedure for optimization based on the combination of efficient quantized tensor train representation and a generalized maximum matrix volume principle. We demonstrate the applicability of the new Tensor Train Optimizer (TTOpt) method for various tasks, ranging from minimization of multidimensional functions to reinforcement learning. Our algorithm compares favorably to popular evolutionary-based methods and outperforms them by the number of function evaluations or execution time, often by a significant margin.
How to Train Unstable Looped Tensor Network
Mar 05, 2022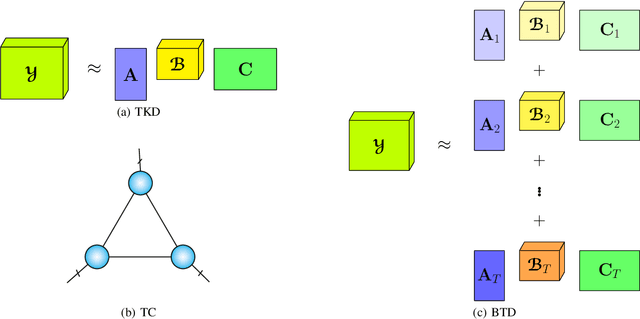
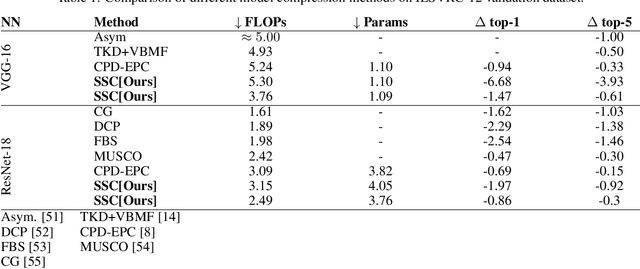
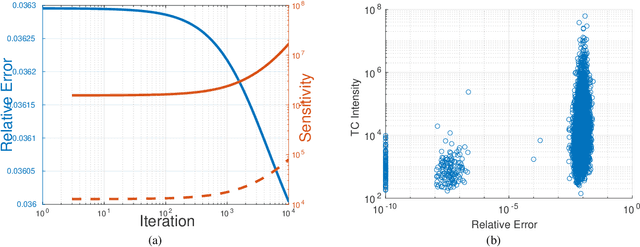
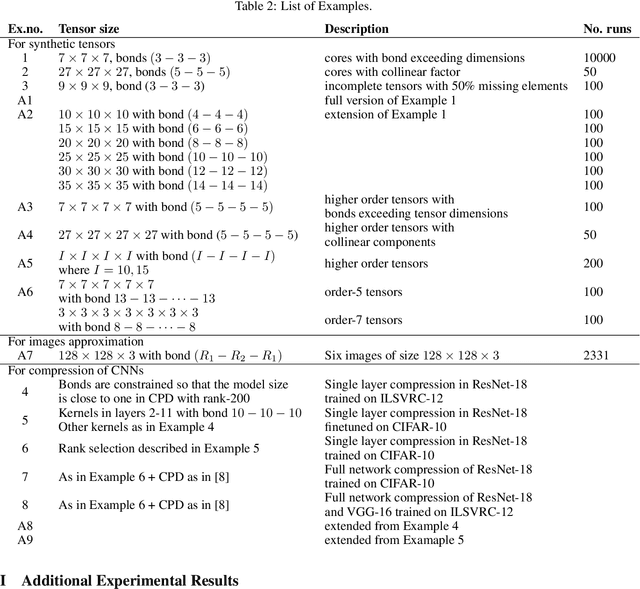
Abstract:A rising problem in the compression of Deep Neural Networks is how to reduce the number of parameters in convolutional kernels and the complexity of these layers by low-rank tensor approximation. Canonical polyadic tensor decomposition (CPD) and Tucker tensor decomposition (TKD) are two solutions to this problem and provide promising results. However, CPD often fails due to degeneracy, making the networks unstable and hard to fine-tune. TKD does not provide much compression if the core tensor is big. This motivates using a hybrid model of CPD and TKD, a decomposition with multiple Tucker models with small core tensor, known as block term decomposition (BTD). This paper proposes a more compact model that further compresses the BTD by enforcing core tensors in BTD identical. We establish a link between the BTD with shared parameters and a looped chain tensor network (TC). Unfortunately, such strongly constrained tensor networks (with loop) encounter severe numerical instability, as proved by y (Landsberg, 2012) and (Handschuh, 2015a). We study perturbation of chain tensor networks, provide interpretation of instability in TC, demonstrate the problem. We propose novel methods to gain the stability of the decomposition results, keep the network robust and attain better approximation. Experimental results will confirm the superiority of the proposed methods in compression of well-known CNNs, and TC decomposition under challenging scenarios
Stable Low-rank Tensor Decomposition for Compression of Convolutional Neural Network
Aug 12, 2020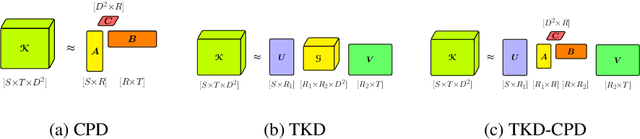
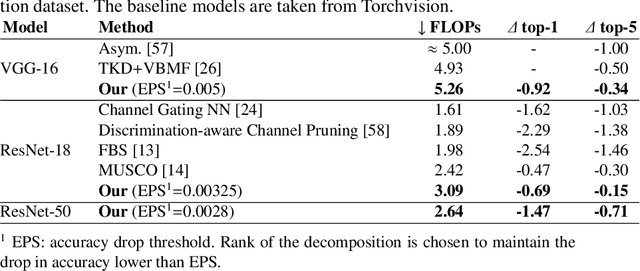
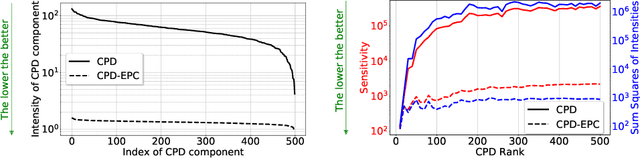
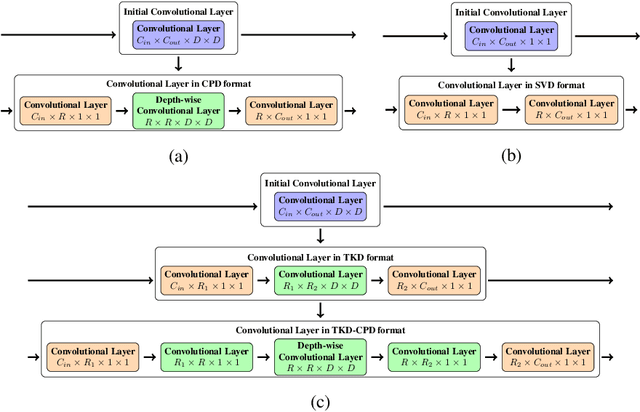
Abstract:Most state of the art deep neural networks are overparameterized and exhibit a high computational cost. A straightforward approach to this problem is to replace convolutional kernels with its low-rank tensor approximations, whereas the Canonical Polyadic tensor Decomposition is one of the most suited models. However, fitting the convolutional tensors by numerical optimization algorithms often encounters diverging components, i.e., extremely large rank-one tensors but canceling each other. Such degeneracy often causes the non-interpretable result and numerical instability for the neural network fine-tuning. This paper is the first study on degeneracy in the tensor decomposition of convolutional kernels. We present a novel method, which can stabilize the low-rank approximation of convolutional kernels and ensure efficient compression while preserving the high-quality performance of the neural networks. We evaluate our approach on popular CNN architectures for image classification and show that our method results in much lower accuracy degradation and provides consistent performance.
CNN Acceleration by Low-rank Approximation with Quantized Factors
Jun 16, 2020



Abstract:The modern convolutional neural networks although achieve great results in solving complex computer vision tasks still cannot be effectively used in mobile and embedded devices due to the strict requirements for computational complexity, memory and power consumption. The CNNs have to be compressed and accelerated before deployment. In order to solve this problem the novel approach combining two known methods, low-rank tensor approximation in Tucker format and quantization of weights and feature maps (activations), is proposed. The greedy one-step and multi-step algorithms for the task of multilinear rank selection are proposed. The approach for quality restoration after applying Tucker decomposition and quantization is developed. The efficiency of our method is demonstrated for ResNet18 and ResNet34 on CIFAR-10, CIFAR-100 and Imagenet classification tasks. As a result of comparative analysis performed for other methods for compression and acceleration our approach showed its promising features.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge