Test-Time Reasoning Through Visual Human Preferences with VLMs and Soft Rewards

Can Visual Language Models (VLMs) effectively capture human visual preferences? This work addresses this question by training VLMs to think about preferences at test time, employing reinforcement learning methods inspired by DeepSeek R1 and OpenAI O1. Using datasets such as ImageReward and Human Preference Score v2 (HPSv2), our models achieve accuracies of 64.9% on the ImageReward test set (trained on ImageReward official split) and 65.4% on HPSv2 (trained on approximately 25% of its data). These results match traditional encoder-based models while providing transparent reasoning and enhanced generalization. This approach allows to use not only rich VLM world knowledge, but also its potential to think, yielding interpretable outcomes that help decision-making processes. By demonstrating that human visual preferences reasonable by current VLMs, we introduce efficient soft-reward strategies for image ranking, outperforming simplistic selection or scoring methods. This reasoning capability enables VLMs to rank arbitrary images-regardless of aspect ratio or complexity-thereby potentially amplifying the effectiveness of visual Preference Optimization. By reducing the need for extensive markup while improving reward generalization and explainability, our findings can be a strong mile-stone that will enhance text-to-vision models even further.

Lightweight Attribute Localizing Models for Pedestrian Attribute Recognition

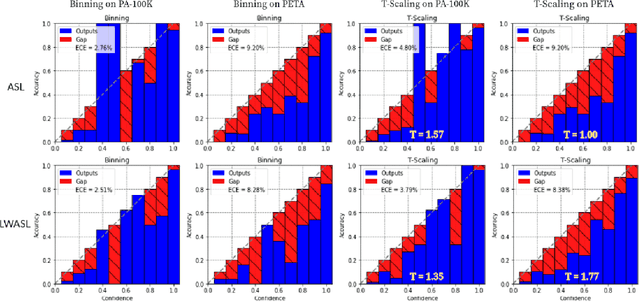
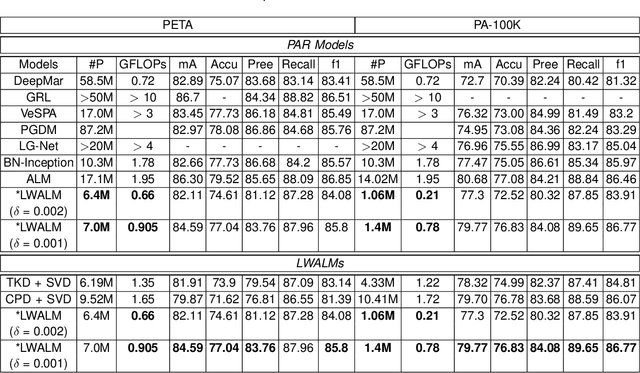
Pedestrian Attribute Recognition (PAR) deals with the problem of identifying features in a pedestrian image. It has found interesting applications in person retrieval, suspect re-identification and soft biometrics. In the past few years, several Deep Neural Networks (DNNs) have been designed to solve the task; however, the developed DNNs predominantly suffer from over-parameterization and high computational complexity. These problems hinder them from being exploited in resource-constrained embedded devices with limited memory and computational capacity. By reducing a network's layers using effective compression techniques, such as tensor decomposition, neural network compression is an effective method to tackle these problems. We propose novel Lightweight Attribute Localizing Models (LWALM) for Pedestrian Attribute Recognition (PAR). LWALM is a compressed neural network obtained after effective layer-wise compression of the Attribute Localization Model (ALM) using the Canonical Polyadic Decomposition with Error Preserving Correction (CPD-EPC) algorithm.

How to Train Unstable Looped Tensor Network

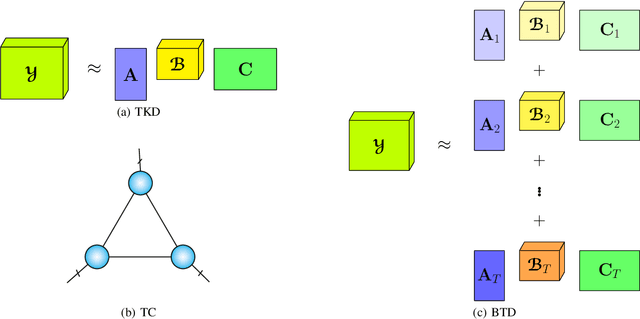
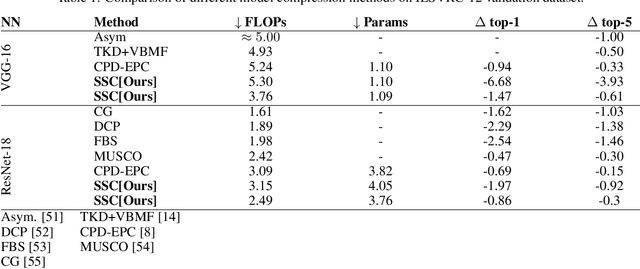
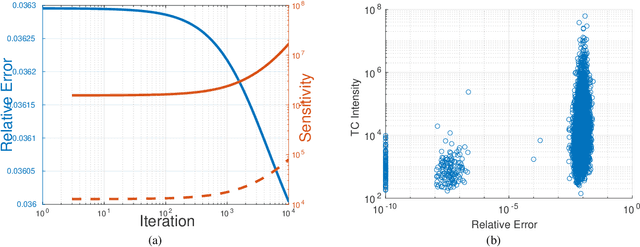
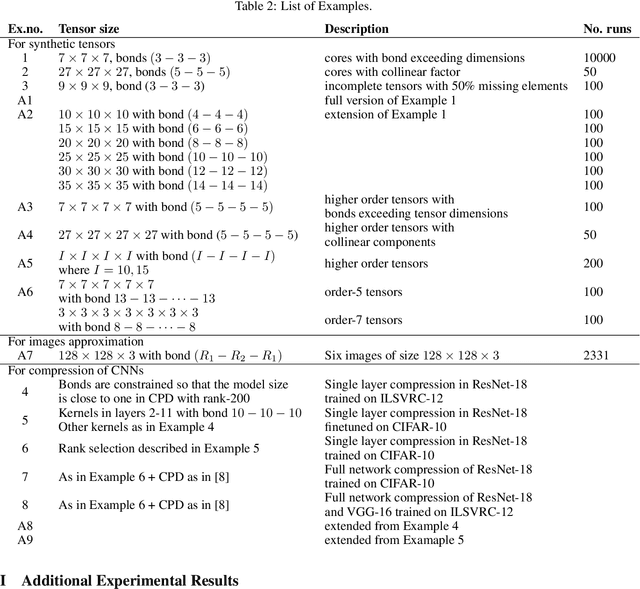
A rising problem in the compression of Deep Neural Networks is how to reduce the number of parameters in convolutional kernels and the complexity of these layers by low-rank tensor approximation. Canonical polyadic tensor decomposition (CPD) and Tucker tensor decomposition (TKD) are two solutions to this problem and provide promising results. However, CPD often fails due to degeneracy, making the networks unstable and hard to fine-tune. TKD does not provide much compression if the core tensor is big. This motivates using a hybrid model of CPD and TKD, a decomposition with multiple Tucker models with small core tensor, known as block term decomposition (BTD). This paper proposes a more compact model that further compresses the BTD by enforcing core tensors in BTD identical. We establish a link between the BTD with shared parameters and a looped chain tensor network (TC). Unfortunately, such strongly constrained tensor networks (with loop) encounter severe numerical instability, as proved by y (Landsberg, 2012) and (Handschuh, 2015a). We study perturbation of chain tensor networks, provide interpretation of instability in TC, demonstrate the problem. We propose novel methods to gain the stability of the decomposition results, keep the network robust and attain better approximation. Experimental results will confirm the superiority of the proposed methods in compression of well-known CNNs, and TC decomposition under challenging scenarios

Stable Low-rank Tensor Decomposition for Compression of Convolutional Neural Network

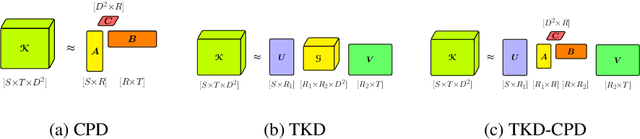
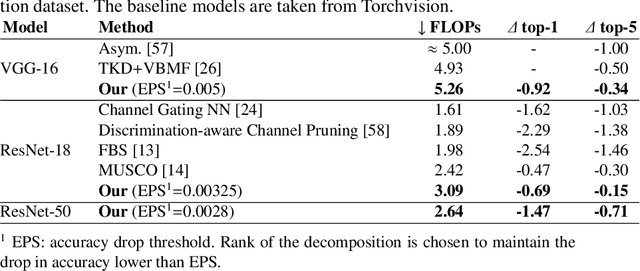
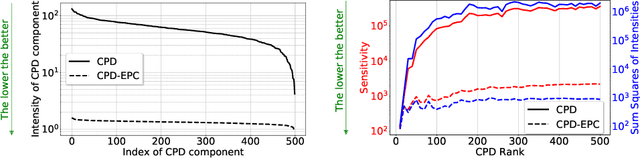
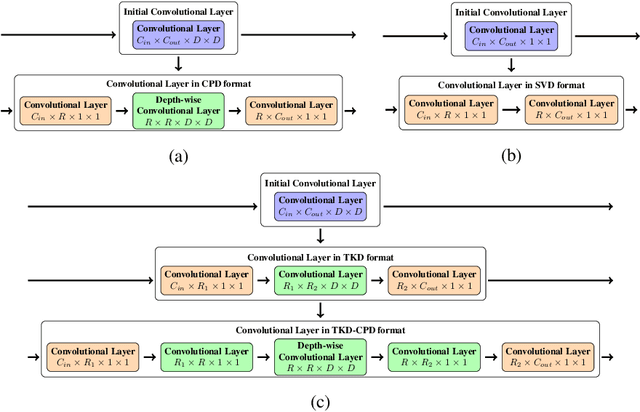
Most state of the art deep neural networks are overparameterized and exhibit a high computational cost. A straightforward approach to this problem is to replace convolutional kernels with its low-rank tensor approximations, whereas the Canonical Polyadic tensor Decomposition is one of the most suited models. However, fitting the convolutional tensors by numerical optimization algorithms often encounters diverging components, i.e., extremely large rank-one tensors but canceling each other. Such degeneracy often causes the non-interpretable result and numerical instability for the neural network fine-tuning. This paper is the first study on degeneracy in the tensor decomposition of convolutional kernels. We present a novel method, which can stabilize the low-rank approximation of convolutional kernels and ensure efficient compression while preserving the high-quality performance of the neural networks. We evaluate our approach on popular CNN architectures for image classification and show that our method results in much lower accuracy degradation and provides consistent performance.