Lightweight Attribute Localizing Models for Pedestrian Attribute Recognition

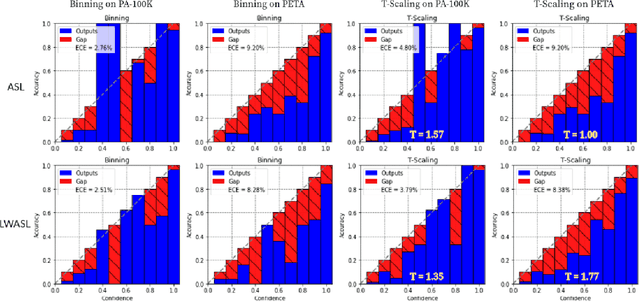
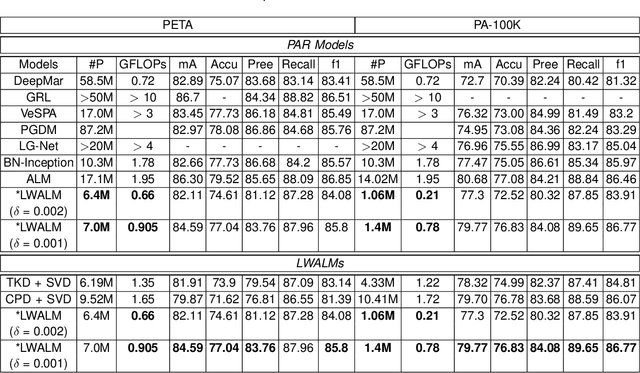
Pedestrian Attribute Recognition (PAR) deals with the problem of identifying features in a pedestrian image. It has found interesting applications in person retrieval, suspect re-identification and soft biometrics. In the past few years, several Deep Neural Networks (DNNs) have been designed to solve the task; however, the developed DNNs predominantly suffer from over-parameterization and high computational complexity. These problems hinder them from being exploited in resource-constrained embedded devices with limited memory and computational capacity. By reducing a network's layers using effective compression techniques, such as tensor decomposition, neural network compression is an effective method to tackle these problems. We propose novel Lightweight Attribute Localizing Models (LWALM) for Pedestrian Attribute Recognition (PAR). LWALM is a compressed neural network obtained after effective layer-wise compression of the Attribute Localization Model (ALM) using the Canonical Polyadic Decomposition with Error Preserving Correction (CPD-EPC) algorithm.

Image Reconstruction using Superpixel Clustering and Tensor Completion

This paper presents a pixel selection method for compact image representation based on superpixel segmentation and tensor completion. Our method divides the image into several regions that capture important textures or semantics and selects a representative pixel from each region to store. We experiment with different criteria for choosing the representative pixel and find that the centroid pixel performs the best. We also propose two smooth tensor completion algorithms that can effectively reconstruct different types of images from the selected pixels. Our experiments show that our superpixel-based method achieves better results than uniform sampling for various missing ratios.

Machine learning models for DOTA 2 outcomes prediction

Prediction of the real-time multiplayer online battle arena (MOBA) games' match outcome is one of the most important and exciting tasks in Esports analytical research. This research paper predominantly focuses on building predictive machine and deep learning models to identify the outcome of the Dota 2 MOBA game using the new method of multi-forward steps predictions. Three models were investigated and compared: Linear Regression (LR), Neural Networks (NN), and a type of recurrent neural network Long Short-Term Memory (LSTM). In order to achieve the goals, we developed a data collecting python server using Game State Integration (GSI) to track the real-time data of the players. Once the exploratory feature analysis and tuning hyper-parameters were done, our models' experiments took place on different players with dissimilar backgrounds of playing experiences. The achieved accuracy scores depend on the multi-forward prediction parameters, which for the worse case in linear regression 69\% but on average 82\%, while in the deep learning models hit the utmost accuracy of prediction on average 88\% for NN, and 93\% for LSTM models.

Deep convolutional tensor network

Tensor networks are linear algebraic representations of quantum many-body states based on their entanglement structure. People are exploring their applications to machine learning. Deep convolutional neural networks achieve state of the art results in computer vision and other areas. Supposedly this happens because of parameter sharing, locality, and deepness. We devise a novel tensor network based model called Deep convolutional tensor network (DCTN) for image classification, which has parameter sharing, locality, and deepness. It is based on the Entangled plaquette states (EPS) tensor network. We show how Entangled plaquette states can be implemented as a backpropagatable layer which can be used in neural networks. We test our model on FashionMNIST dataset and find that deepness increases overfitting and decreases test accuracy. Also, we find that the shallow version performs well considering its low parameter count. We discuss how hyperparameters of DCTN affect its training and overfitting.

Low Complexity Damped Gauss-Newton Algorithms for CANDECOMP/PARAFAC

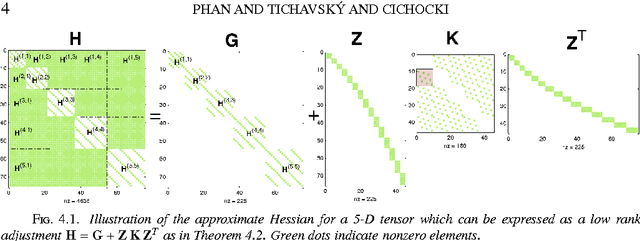
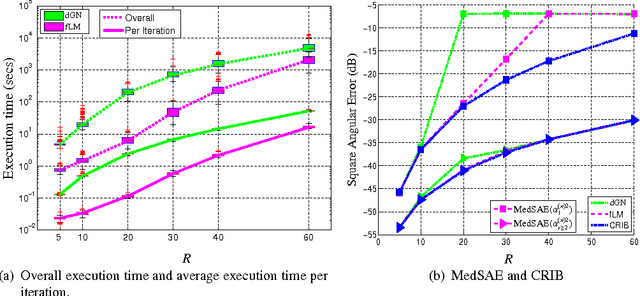
The damped Gauss-Newton (dGN) algorithm for CANDECOMP/PARAFAC (CP) decomposition can handle the challenges of collinearity of factors and different magnitudes of factors; nevertheless, for factorization of an $N$-D tensor of size $I_1\times I_N$ with rank $R$, the algorithm is computationally demanding due to construction of large approximate Hessian of size $(RT \times RT)$ and its inversion where $T = \sum_n I_n$. In this paper, we propose a fast implementation of the dGN algorithm which is based on novel expressions of the inverse approximate Hessian in block form. The new implementation has lower computational complexity, besides computation of the gradient (this part is common to both methods), requiring the inversion of a matrix of size $NR^2\times NR^2$, which is much smaller than the whole approximate Hessian, if $T \gg NR$. In addition, the implementation has lower memory requirements, because neither the Hessian nor its inverse never need to be stored in their entirety. A variant of the algorithm working with complex valued data is proposed as well. Complexity and performance of the proposed algorithm is compared with those of dGN and ALS with line search on examples of difficult benchmark tensors.