Double Nonstationarity: Blind Extraction of Independent Nonstationary Vector/Component from Nonstationary Mixtures -- Algorithms

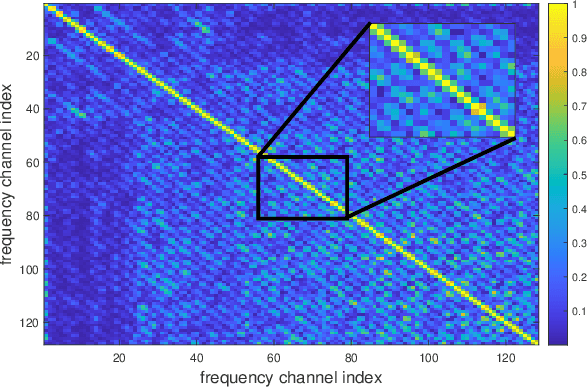
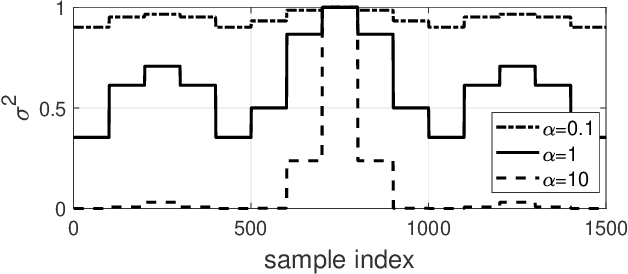
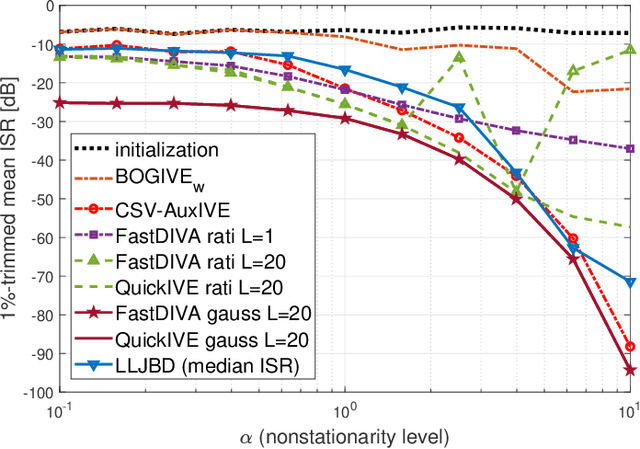
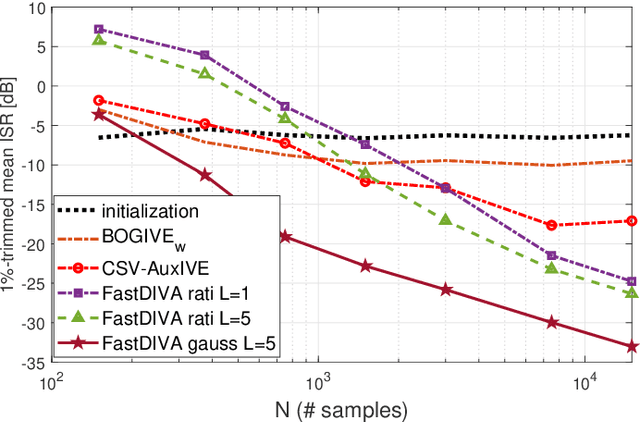
In this article, nonstationary mixing and source models are combined for developing new fast and accurate algorithms for Independent Component or Vector Extraction (ICE/IVE), one of which stands for a new extension of the well-known FastICA. This model allows for a moving source-of-interest (SOI) whose distribution on short intervals can be (non-)circular (non-)Gaussian. A particular Gaussian source model assuming tridiagonal covariance matrix structures is proposed. It is shown to be beneficial in the frequency-domain speaker extraction problem. The algorithms are verified in simulations. In comparison to the state-of-the-art algorithms, they show superior performance in terms of convergence speed and extraction accuracy.

On tensor rank of conditional probability tables in Bayesian networks

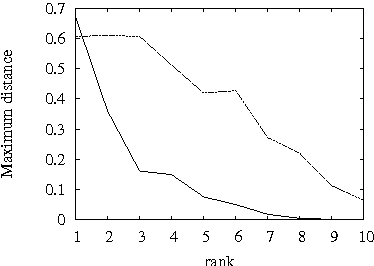
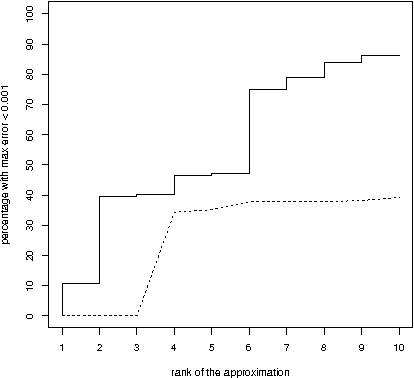
A difficult task in modeling with Bayesian networks is the elicitation of numerical parameters of Bayesian networks. A large number of parameters is needed to specify a conditional probability table (CPT) that has a larger parent set. In this paper we show that, most CPTs from real applications of Bayesian networks can actually be very well approximated by tables that require substantially less parameters. This observation has practical consequence not only for model elicitation but also for efficient probabilistic reasoning with these networks.

Low Complexity Damped Gauss-Newton Algorithms for CANDECOMP/PARAFAC

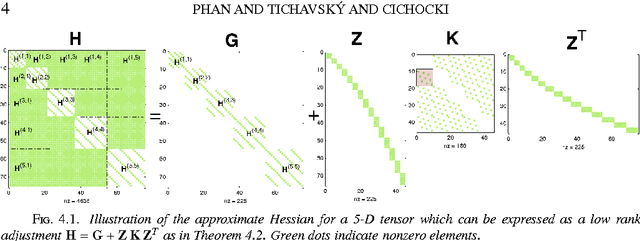
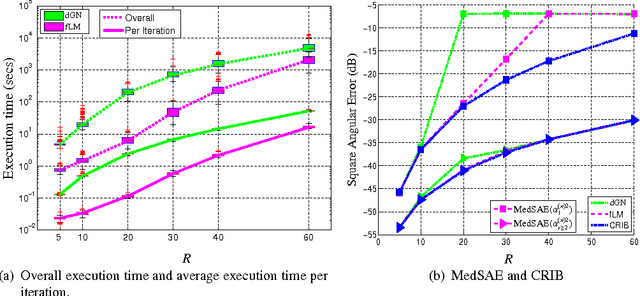
The damped Gauss-Newton (dGN) algorithm for CANDECOMP/PARAFAC (CP) decomposition can handle the challenges of collinearity of factors and different magnitudes of factors; nevertheless, for factorization of an $N$-D tensor of size $I_1\times I_N$ with rank $R$, the algorithm is computationally demanding due to construction of large approximate Hessian of size $(RT \times RT)$ and its inversion where $T = \sum_n I_n$. In this paper, we propose a fast implementation of the dGN algorithm which is based on novel expressions of the inverse approximate Hessian in block form. The new implementation has lower computational complexity, besides computation of the gradient (this part is common to both methods), requiring the inversion of a matrix of size $NR^2\times NR^2$, which is much smaller than the whole approximate Hessian, if $T \gg NR$. In addition, the implementation has lower memory requirements, because neither the Hessian nor its inverse never need to be stored in their entirety. A variant of the algorithm working with complex valued data is proposed as well. Complexity and performance of the proposed algorithm is compared with those of dGN and ALS with line search on examples of difficult benchmark tensors.