Dynamic Independent Component Extraction with Blending Mixing Vector: Lower Bound on Mean Interference-to-Signal Ratio

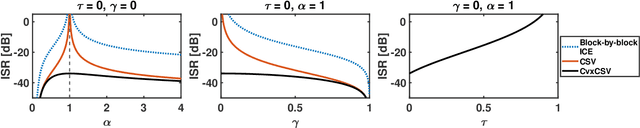
This paper deals with dynamic Blind Source Extraction (BSE) from where the mixing parameters characterizing the position of a source of interest (SOI) are allowed to vary over time. We present a new source extraction model called CvxCSV which is a parameter-reduced modification of the recent Constant Separation Vector (CSV) mixing model. In CvxCSV, the mixing vector evolves as a convex combination of its initial and final values. We derive a lower bound on the achievable mean interference-to-signal ratio (ISR) based on the Cram\'er-Rao theory. The bound reveals advantageous properties of CvxCSV compared with CSV and compared with a sequential BSE based on independent component extraction (ICE). In particular, the achievable ISR by CvxCSV is lower than that by the previous approaches. Moreover, the model requires significantly weaker conditions for identifiability, even when the SOI is Gaussian.

Double Nonstationarity: Blind Extraction of Independent Nonstationary Vector/Component from Nonstationary Mixtures -- Algorithms

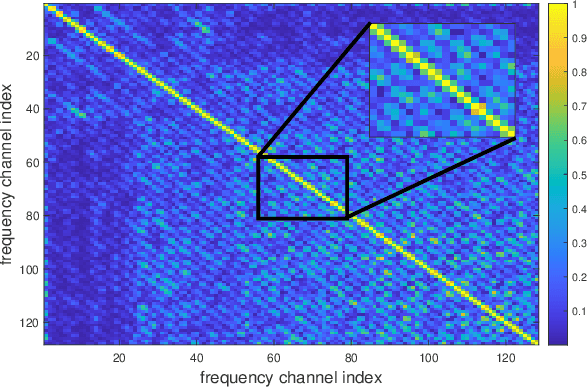
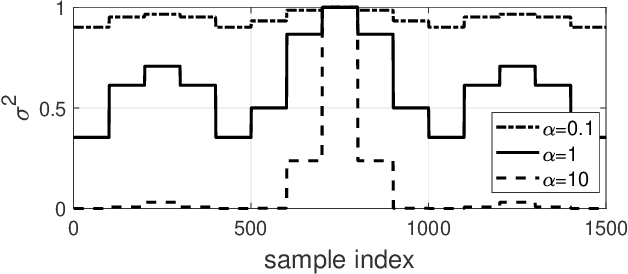
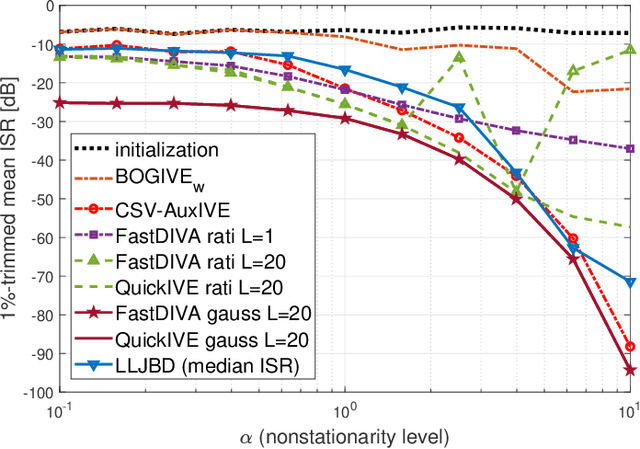
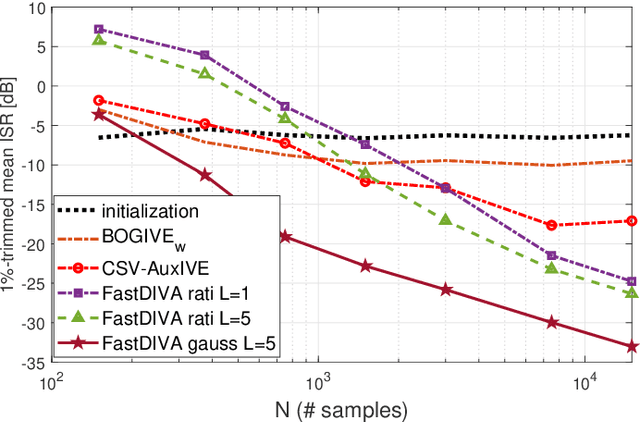
In this article, nonstationary mixing and source models are combined for developing new fast and accurate algorithms for Independent Component or Vector Extraction (ICE/IVE), one of which stands for a new extension of the well-known FastICA. This model allows for a moving source-of-interest (SOI) whose distribution on short intervals can be (non-)circular (non-)Gaussian. A particular Gaussian source model assuming tridiagonal covariance matrix structures is proposed. It is shown to be beneficial in the frequency-domain speaker extraction problem. The algorithms are verified in simulations. In comparison to the state-of-the-art algorithms, they show superior performance in terms of convergence speed and extraction accuracy.