Blind Capon Beamformer Based on Independent Component Extraction: Single-Parameter Algorithm,

We consider a phase-shift mixing model for linear sensor arrays in the context of blind source extraction. We derive a blind Capon beamformer that seeks the direction where the output is independent of the other signals in the mixture. The algorithm is based on Independent Component Extraction and imposes an orthogonal constraint, thanks to which it optimizes only one real-valued parameter related to the angle of arrival. The Cram\'er-Rao lower bound for the mean interference-to-signal ratio is derived. The algorithm and the bound are compared with conventional blind and direction-of-arrival estimation+beamforming methods, showing improvements in terms of extraction accuracy. An application is demonstrated in frequency-domain speaker extraction in a low-reverberation room.

Informed FastICA: Semi-Blind Minimum Variance Distortionless Beamformer

Non-Gaussianity-based Independent Vector Extraction leads to the famous one-unit FastICA/FastIVA algorithm when the likelihood function is optimized using an approximate Newton-Raphson algorithm under the orthogonality constraint. In this paper, we replace the constraint with the analytic form of the minimum variance distortionless beamformer (MVDR), by which a semi-blind variant of FastICA/FastIVA is obtained. The side information here is provided by a weighted covariance matrix replacing the noise covariance matrix, the estimation of which is a frequent goal of neural beamformers. The algorithm thus provides an intuitive connection between model-based blind extraction and learning-based extraction. The algorithm is tested in simulations and speaker ID-guided speaker extraction, showing fast convergence and promising performance.

Independent Vector Extraction Constrained on Manifold of Half-Length Filters

Independent Vector Analysis (IVA) is a popular extension of Independent Component Analysis (ICA) for joint separation of a set of instantaneous linear mixtures, with a direct application in frequency-domain speaker separation or extraction. The mixtures are parameterized by mixing matrices, one matrix per mixture. This means that the IVA mixing model does not account for any relationships between parameters across the mixtures/frequencies. The separation proceeds jointly only through the source model, where statistical dependencies of sources across the mixtures are taken into account. In this paper, we propose a mixing model for joint blind source extraction where the mixing model parameters are linked across the frequencies. This is achieved by constraining the set of feasible parameters to the manifold of half-length separating filters, which has a clear interpretation and application in frequency-domain speaker extraction.

Dynamic Independent Component Extraction with Blending Mixing Vector: Lower Bound on Mean Interference-to-Signal Ratio

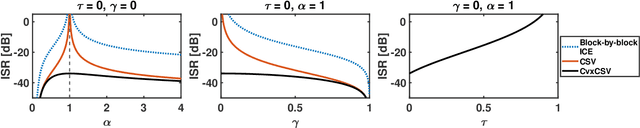
This paper deals with dynamic Blind Source Extraction (BSE) from where the mixing parameters characterizing the position of a source of interest (SOI) are allowed to vary over time. We present a new source extraction model called CvxCSV which is a parameter-reduced modification of the recent Constant Separation Vector (CSV) mixing model. In CvxCSV, the mixing vector evolves as a convex combination of its initial and final values. We derive a lower bound on the achievable mean interference-to-signal ratio (ISR) based on the Cram\'er-Rao theory. The bound reveals advantageous properties of CvxCSV compared with CSV and compared with a sequential BSE based on independent component extraction (ICE). In particular, the achievable ISR by CvxCSV is lower than that by the previous approaches. Moreover, the model requires significantly weaker conditions for identifiability, even when the SOI is Gaussian.