Independent Vector Extraction Constrained on Manifold of Half-Length Filters

Independent Vector Analysis (IVA) is a popular extension of Independent Component Analysis (ICA) for joint separation of a set of instantaneous linear mixtures, with a direct application in frequency-domain speaker separation or extraction. The mixtures are parameterized by mixing matrices, one matrix per mixture. This means that the IVA mixing model does not account for any relationships between parameters across the mixtures/frequencies. The separation proceeds jointly only through the source model, where statistical dependencies of sources across the mixtures are taken into account. In this paper, we propose a mixing model for joint blind source extraction where the mixing model parameters are linked across the frequencies. This is achieved by constraining the set of feasible parameters to the manifold of half-length separating filters, which has a clear interpretation and application in frequency-domain speaker extraction.

Dynamic Independent Component Extraction with Blending Mixing Vector: Lower Bound on Mean Interference-to-Signal Ratio

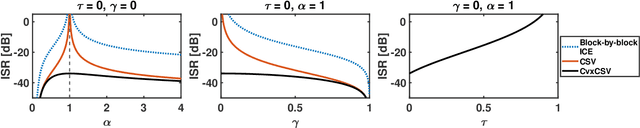
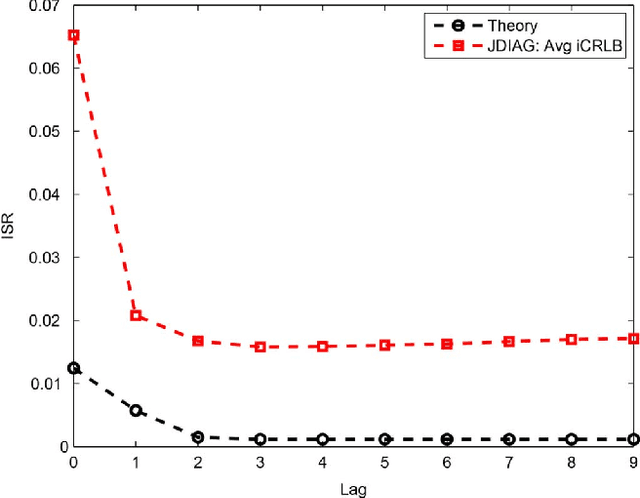
This paper deals with dynamic Blind Source Extraction (BSE) from where the mixing parameters characterizing the position of a source of interest (SOI) are allowed to vary over time. We present a new source extraction model called CvxCSV which is a parameter-reduced modification of the recent Constant Separation Vector (CSV) mixing model. In CvxCSV, the mixing vector evolves as a convex combination of its initial and final values. We derive a lower bound on the achievable mean interference-to-signal ratio (ISR) based on the Cram\'er-Rao theory. The bound reveals advantageous properties of CvxCSV compared with CSV and compared with a sequential BSE based on independent component extraction (ICE). In particular, the achievable ISR by CvxCSV is lower than that by the previous approaches. Moreover, the model requires significantly weaker conditions for identifiability, even when the SOI is Gaussian.

Independent Component Analysis for Trustworthy Cyberspace during High Impact Events: An Application to Covid-19

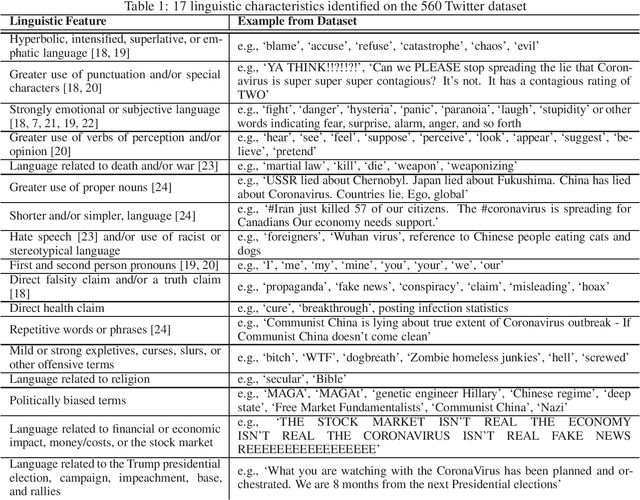
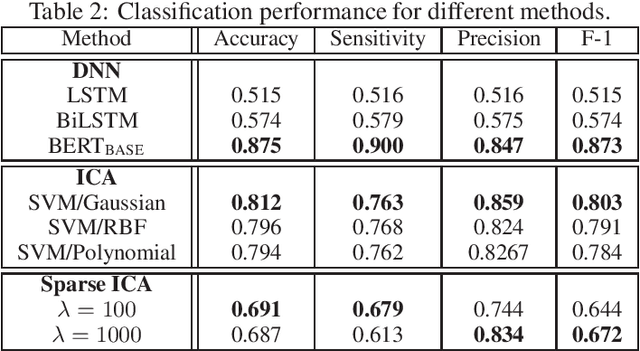
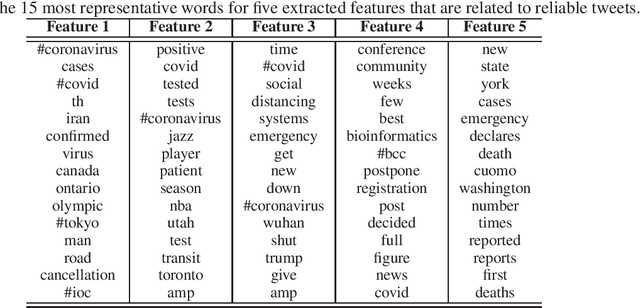
Social media has become an important communication channel during high impact events, such as the COVID-19 pandemic. As misinformation in social media can rapidly spread, creating social unrest, curtailing the spread of misinformation during such events is a significant data challenge. While recent solutions that are based on machine learning have shown promise for the detection of misinformation, most widely used methods include approaches that rely on either handcrafted features that cannot be optimal for all scenarios, or those that are based on deep learning where the interpretation of the prediction results is not directly accessible. In this work, we propose a data-driven solution that is based on the ICA model, such that knowledge discovery and detection of misinformation are achieved jointly. To demonstrate the effectiveness of our method and compare its performance with deep learning methods, we developed a labeled COVID-19 Twitter dataset based on socio-linguistic criteria.

Tracing Network Evolution Using the PARAFAC2 Model

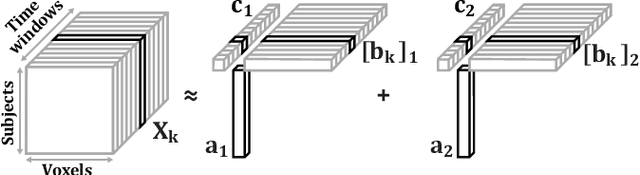
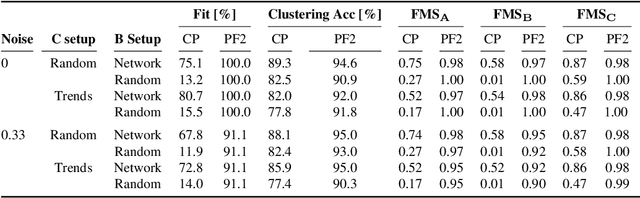
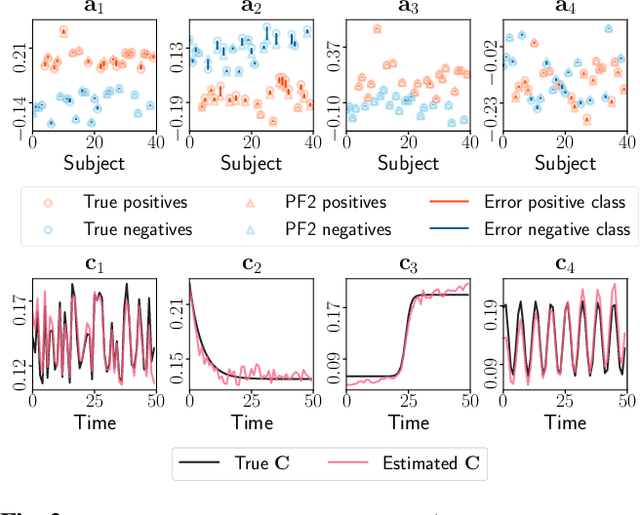
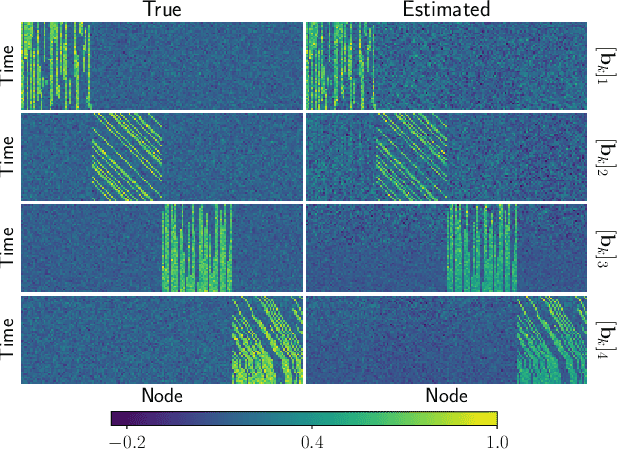
Characterizing time-evolving networks is a challenging task, but it is crucial for understanding the dynamic behavior of complex systems such as the brain. For instance, how spatial networks of functional connectivity in the brain evolve during a task is not well-understood. A traditional approach in neuroimaging data analysis is to make simplifications through the assumption of static spatial networks. In this paper, without assuming static networks in time and/or space, we arrange the temporal data as a higher-order tensor and use a tensor factorization model called PARAFAC2 to capture underlying patterns (spatial networks) in time-evolving data and their evolution. Numerical experiments on simulated data demonstrate that PARAFAC2 can successfully reveal the underlying networks and their dynamics. We also show the promising performance of the model in terms of tracing the evolution of task-related functional connectivity in the brain through the analysis of functional magnetic resonance imaging data.

Tensor-Based Fusion of EEG and FMRI to Understand Neurological Changes in Schizophrenia

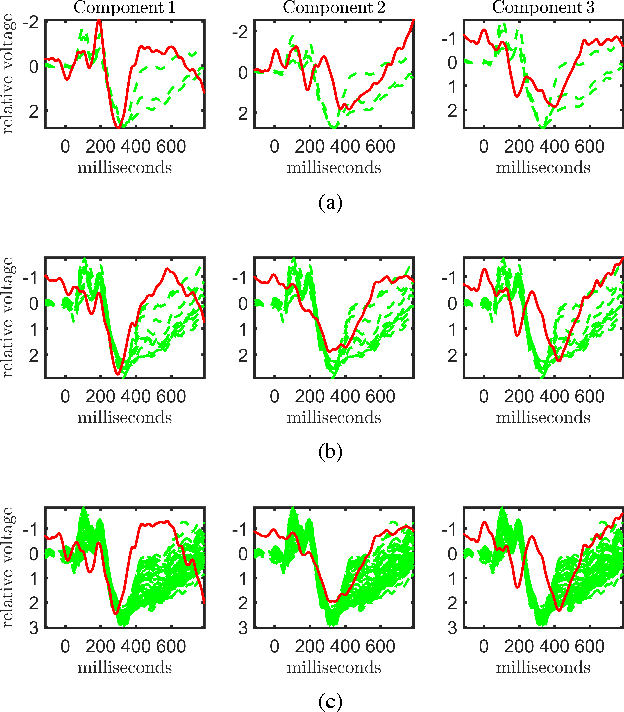
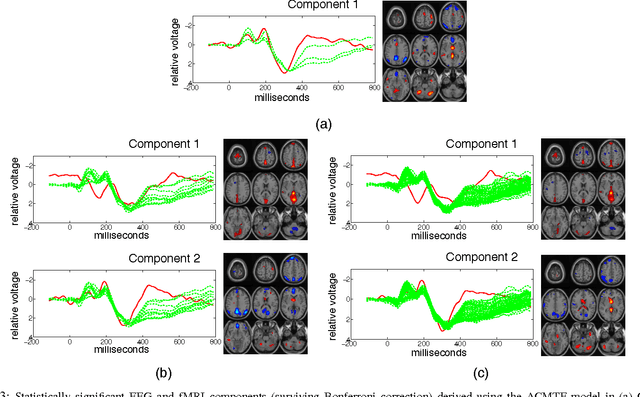
Neuroimaging modalities such as functional magnetic resonance imaging (fMRI) and electroencephalography (EEG) provide information about neurological functions in complementary spatiotemporal resolutions; therefore, fusion of these modalities is expected to provide better understanding of brain activity. In this paper, we jointly analyze fMRI and multi-channel EEG signals collected during an auditory oddball task with the goal of capturing brain activity patterns that differ between patients with schizophrenia and healthy controls. Rather than selecting a single electrode or matricizing the third-order tensor that can be naturally used to represent multi-channel EEG signals, we preserve the multi-way structure of EEG data and use a coupled matrix and tensor factorization (CMTF) model to jointly analyze fMRI and EEG signals. Our analysis reveals that (i) joint analysis of EEG and fMRI using a CMTF model can capture meaningful temporal and spatial signatures of patterns that behave differently in patients and controls, and (ii) these differences and the interpretability of the associated components increase by including multiple electrodes from frontal, motor and parietal areas, but not necessarily by including all electrodes in the analysis.

Linked Component Analysis from Matrices to High Order Tensors: Applications to Biomedical Data

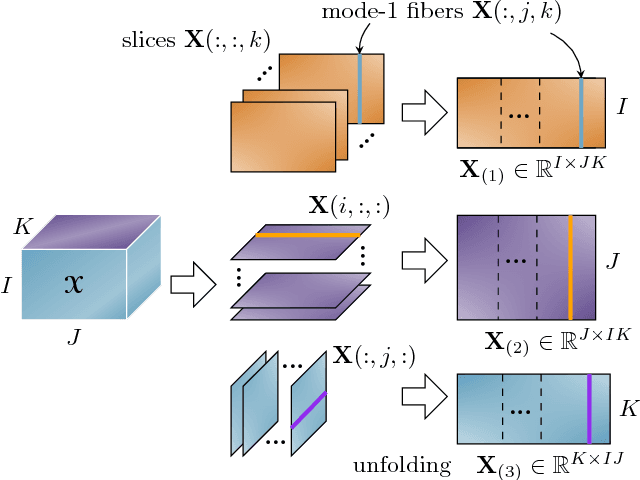
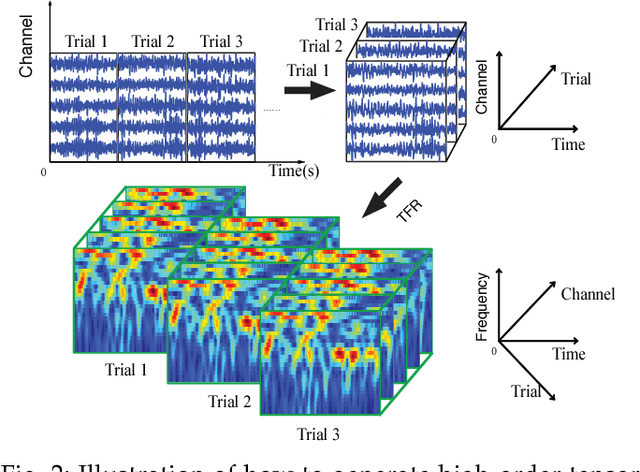
With the increasing availability of various sensor technologies, we now have access to large amounts of multi-block (also called multi-set, multi-relational, or multi-view) data that need to be jointly analyzed to explore their latent connections. Various component analysis methods have played an increasingly important role for the analysis of such coupled data. In this paper, we first provide a brief review of existing matrix-based (two-way) component analysis methods for the joint analysis of such data with a focus on biomedical applications. Then, we discuss their important extensions and generalization to multi-block multiway (tensor) data. We show how constrained multi-block tensor decomposition methods are able to extract similar or statistically dependent common features that are shared by all blocks, by incorporating the multiway nature of data. Special emphasis is given to the flexible common and individual feature analysis of multi-block data with the aim to simultaneously extract common and individual latent components with desired properties and types of diversity. Illustrative examples are given to demonstrate their effectiveness for biomedical data analysis.

Independent Vector Analysis: Identification Conditions and Performance Bounds

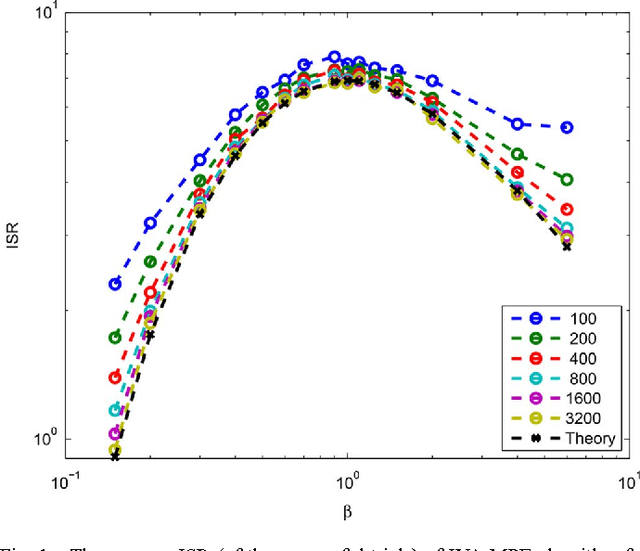
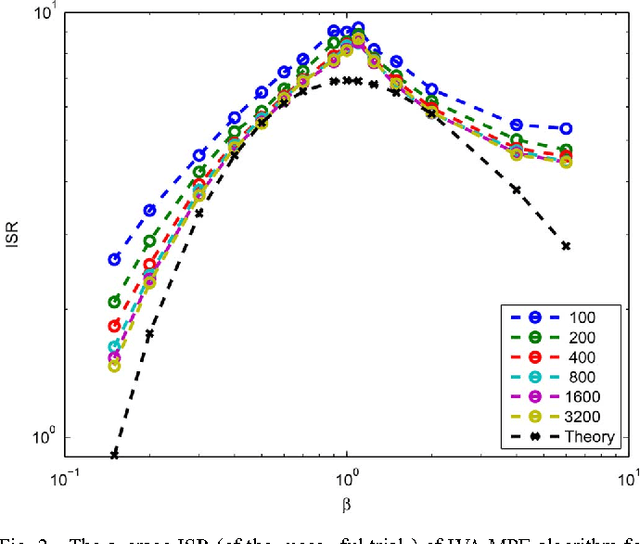
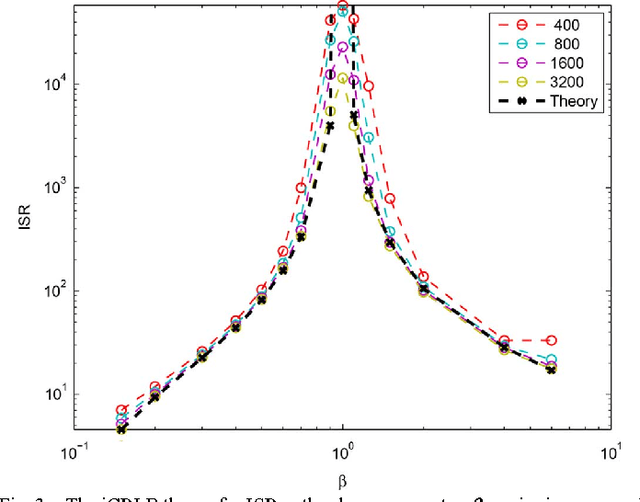
Recently, an extension of independent component analysis (ICA) from one to multiple datasets, termed independent vector analysis (IVA), has been the subject of significant research interest. IVA has also been shown to be a generalization of Hotelling's canonical correlation analysis. In this paper, we provide the identification conditions for a general IVA formulation, which accounts for linear, nonlinear, and sample-to-sample dependencies. The identification conditions are a generalization of previous results for ICA and for IVA when samples are independently and identically distributed. Furthermore, a principal aim of IVA is the identification of dependent sources between datasets. Thus, we provide the additional conditions for when the arbitrary ordering of the sources within each dataset is common. Performance bounds in terms of the Cramer-Rao lower bound are also provided for the demixing matrices and interference to source ratio. The performance of two IVA algorithms are compared to the theoretical bounds.