Single Image Reflection Removal via inter-layer Complementarity

Although dual-stream architectures have achieved remarkable success in single image reflection removal, they fail to fully exploit inter-layer complementarity in their physical modeling and network design, which limits the quality of image separation. To address this fundamental limitation, we propose two targeted improvements to enhance dual-stream architectures: First, we introduce a novel inter-layer complementarity model where low-frequency components extracted from the residual layer interact with the transmission layer through dual-stream architecture to enhance inter-layer complementarity. Meanwhile, high-frequency components from the residual layer provide inverse modulation to both streams, improving the detail quality of the transmission layer. Second, we propose an efficient inter-layer complementarity attention mechanism which first cross-reorganizes dual streams at the channel level to obtain reorganized streams with inter-layer complementary structures, then performs attention computation on the reorganized streams to achieve better inter-layer separation, and finally restores the original stream structure for output. Experimental results demonstrate that our method achieves state-of-the-art separation quality on multiple public datasets while significantly reducing both computational cost and model complexity.

Scaling Capability in Token Space: An Analysis of Large Vision Language Model

The scaling capability has been widely validated in neural language models with respect to the number of parameters and the size of training data. One important question is that does the scaling capability also exists similarly with respect to the number of vision tokens in large vision language Model? This study fills the gap by investigating the relationship between the number of vision tokens and the performance on vision-language models. Our theoretical analysis and empirical evaluations demonstrate that the model exhibits scalable performance \(S(N_l)\) with respect to the number of vision tokens \(N_l\), characterized by the relationship \(S(N_l) \approx (c/N_l)^{\alpha}\). Furthermore, we also investigate the impact of a fusion mechanism that integrates the user's question with vision tokens. The results reveal two key findings. First, the scaling capability remains intact with the incorporation of the fusion mechanism. Second, the fusion mechanism enhances model performance, particularly when the user's question is task-specific and relevant. The analysis, conducted on fifteen diverse benchmarks spanning a broad range of tasks and domains, validates the effectiveness of the proposed approach.

Weak Scaling Capability in Token Space: An Observation from Large Vision Language Model

The scaling capability has been widely validated with respect to the number of parameters and the size of training data. One important question that is unexplored is that does scaling capability also exists similarly with respect to the number of vision tokens? This study fills the gap by investigating the relationship between the number of vision tokens and the performance of vision-language models. Our theoretical analysis and empirical evaluations reveal that the model exhibits weak scaling capabilities on the length \(N_l\), with performance approximately \(S(N_l) \approx (c/N_l)^{\alpha}\), where \(c, \alpha\) are hyperparameters. Interestingly, this scaling behavior remains largely unaffected by the inclusion or exclusion of the user's question in the input. Furthermore, fusing the user's question with the vision token can enhance model performance when the question is relevant to the task. To address the computational challenges associated with large-scale vision tokens, we propose a novel architecture that efficiently reduces the token count while integrating user question tokens into the representation. Our findings may offer insights for developing more efficient and effective vision-language models under specific task constraints.

Discovering More Effective Tensor Network Structure Search Algorithms via Large Language Models (LLMs)

Tensor network structure search (TN-SS), aiming at searching for suitable tensor network (TN) structures in representing high-dimensional problems, largely promotes the efficacy of TN in various machine learning applications. Nonetheless, finding a satisfactory TN structure using existing algorithms remains challenging. To develop more effective algorithms and avoid the human labor-intensive development process, we explore the knowledge embedded in large language models (LLMs) for the automatic design of TN-SS algorithms. Our approach, dubbed GPTN-SS, leverages an elaborate crafting LLM-based prompting system that operates in an evolutionary-like manner. The experimental results, derived from real-world data, demonstrate that GPTN-SS can effectively leverage the insights gained from existing methods to develop novel TN-SS algorithms that achieve a better balance between exploration and exploitation. These algorithms exhibit superior performance in searching the high-quality TN structures for natural image compression and model parameters compression while also demonstrating generalizability in their performance.

Semi-supervised multi-view concept decomposition

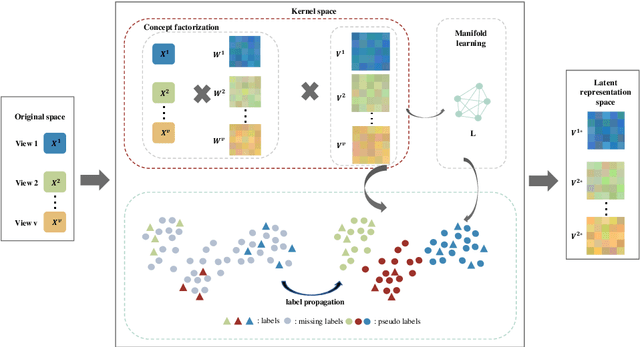
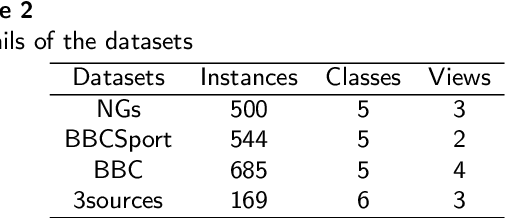
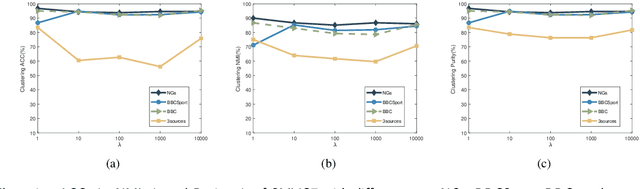
Concept Factorization (CF), as a novel paradigm of representation learning, has demonstrated superior performance in multi-view clustering tasks. It overcomes limitations such as the non-negativity constraint imposed by traditional matrix factorization methods and leverages kernel methods to learn latent representations that capture the underlying structure of the data, thereby improving data representation. However, existing multi-view concept factorization methods fail to consider the limited labeled information inherent in real-world multi-view data. This often leads to significant performance loss. To overcome these limitations, we propose a novel semi-supervised multi-view concept factorization model, named SMVCF. In the SMVCF model, we first extend the conventional single-view CF to a multi-view version, enabling more effective exploration of complementary information across multiple views. We then integrate multi-view CF, label propagation, and manifold learning into a unified framework to leverage and incorporate valuable information present in the data. Additionally, an adaptive weight vector is introduced to balance the importance of different views in the clustering process. We further develop targeted optimization methods specifically tailored for the SMVCF model. Finally, we conduct extensive experiments on four diverse datasets with varying label ratios to evaluate the performance of SMVCF. The experimental results demonstrate the effectiveness and superiority of our proposed approach in multi-view clustering tasks.

Transformed Low-Rank Parameterization Can Help Robust Generalization for Tensor Neural Networks

Achieving efficient and robust multi-channel data learning is a challenging task in data science. By exploiting low-rankness in the transformed domain, i.e., transformed low-rankness, tensor Singular Value Decomposition (t-SVD) has achieved extensive success in multi-channel data representation and has recently been extended to function representation such as Neural Networks with t-product layers (t-NNs). However, it still remains unclear how t-SVD theoretically affects the learning behavior of t-NNs. This paper is the first to answer this question by deriving the upper bounds of the generalization error of both standard and adversarially trained t-NNs. It reveals that the t-NNs compressed by exact transformed low-rank parameterization can achieve a sharper adversarial generalization bound. In practice, although t-NNs rarely have exactly transformed low-rank weights, our analysis further shows that by adversarial training with gradient flow (GF), the over-parameterized t-NNs with ReLU activations are trained with implicit regularization towards transformed low-rank parameterization under certain conditions. We also establish adversarial generalization bounds for t-NNs with approximately transformed low-rank weights. Our analysis indicates that the transformed low-rank parameterization can promisingly enhance robust generalization for t-NNs.

Towards Efficient and Accurate Approximation: Tensor Decomposition Based on Randomized Block Krylov Iteration

Efficient and accurate low-rank approximation (LRA) methods are of great significance for large-scale data analysis. Randomized tensor decompositions have emerged as powerful tools to meet this need, but most existing methods perform poorly in the presence of noise interference. Inspired by the remarkable performance of randomized block Krylov iteration (rBKI) in reducing the effect of tail singular values, this work designs an rBKI-based Tucker decomposition (rBKI-TK) for accurate approximation, together with a hierarchical tensor ring decomposition based on rBKI-TK for efficient compression of large-scale data. Besides, the error bound between the deterministic LRA and the randomized LRA is studied. Numerical experiences demonstrate the efficiency, accuracy and scalability of the proposed methods in both data compression and denoising.

Latent Matrices for Tensor Network Decomposition and to Tensor Completion

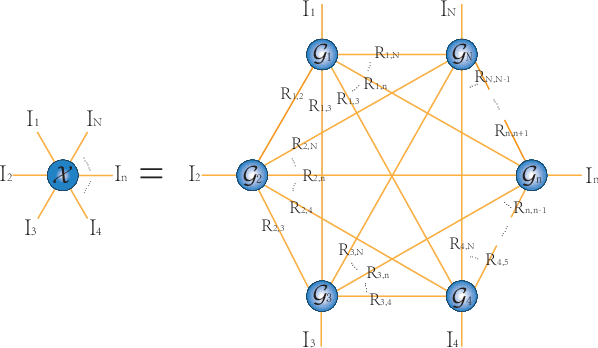
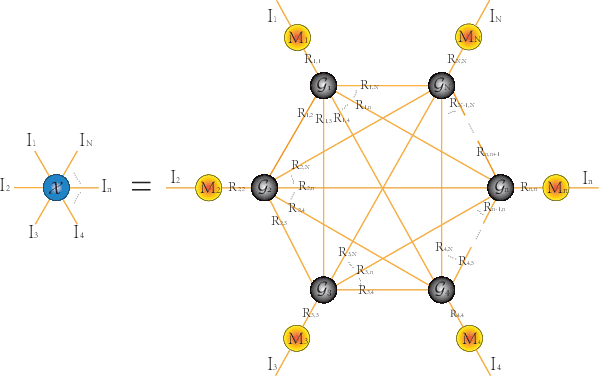
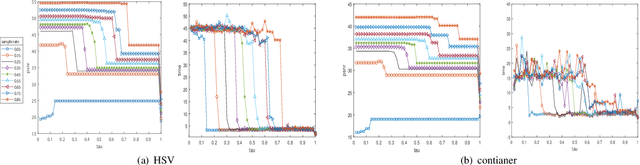
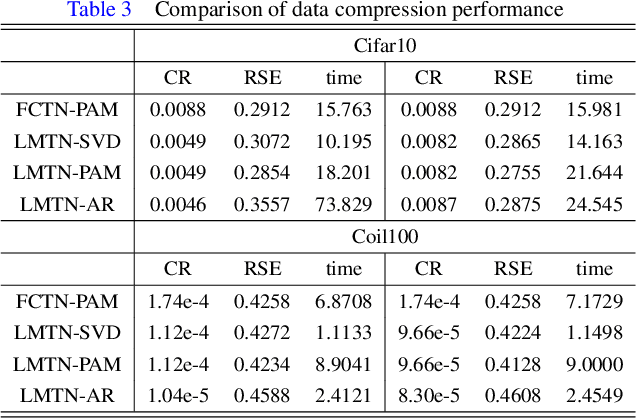
The prevalent fully-connected tensor network (FCTN) has achieved excellent success to compress data. However, the FCTN decomposition suffers from slow computational speed when facing higher-order and large-scale data. Naturally, there arises an interesting question: can a new model be proposed that decomposes the tensor into smaller ones and speeds up the computation of the algorithm? This work gives a positive answer by formulating a novel higher-order tensor decomposition model that utilizes latent matrices based on the tensor network structure, which can decompose a tensor into smaller-scale data than the FCTN decomposition, hence we named it Latent Matrices for Tensor Network Decomposition (LMTN). Furthermore, three optimization algorithms, LMTN-PAM, LMTN-SVD and LMTN-AR, have been developed and applied to the tensor-completion task. In addition, we provide proofs of theoretical convergence and complexity analysis for these algorithms. Experimental results show that our algorithm has the effectiveness in both deep learning dataset compression and higher-order tensor completion, and that our LMTN-SVD algorithm is 3-6 times faster than the FCTN-PAM algorithm and only a 1.8 points accuracy drop.

A high-order tensor completion algorithm based on Fully-Connected Tensor Network weighted optimization

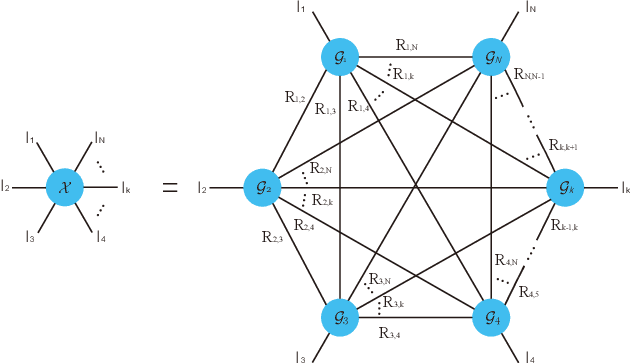
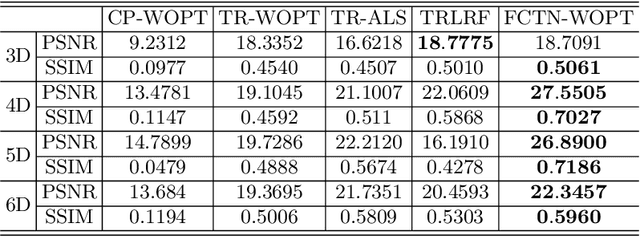
Tensor completion aimes at recovering missing data, and it is one of the popular concerns in deep learning and signal processing. Among the higher-order tensor decomposition algorithms, the recently proposed fully-connected tensor network decomposition (FCTN) algorithm is the most advanced. In this paper, by leveraging the superior expression of the fully-connected tensor network (FCTN) decomposition, we propose a new tensor completion method named the fully connected tensor network weighted optization(FCTN-WOPT). The algorithm performs a composition of the completed tensor by initialising the factors from the FCTN decomposition. We build a loss function with the weight tensor, the completed tensor and the incomplete tensor together, and then update the completed tensor using the lbfgs gradient descent algorithm to reduce the spatial memory occupation and speed up iterations. Finally we test the completion with synthetic data and real data (both image data and video data) and the results show the advanced performance of our FCTN-WOPT when it is applied to higher-order tensor completion.

Noisy Tensor Completion via Low-rank Tensor Ring

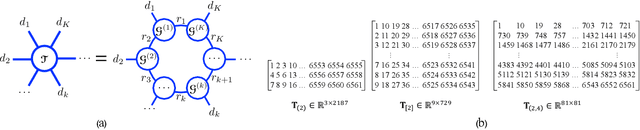
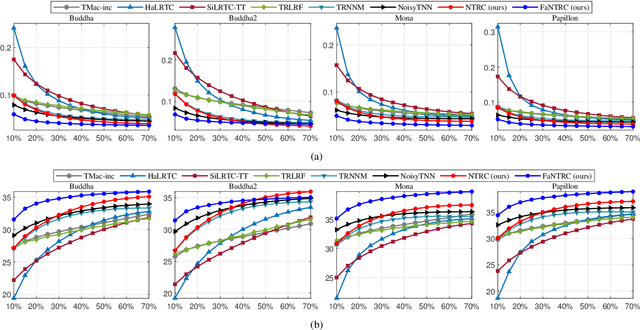
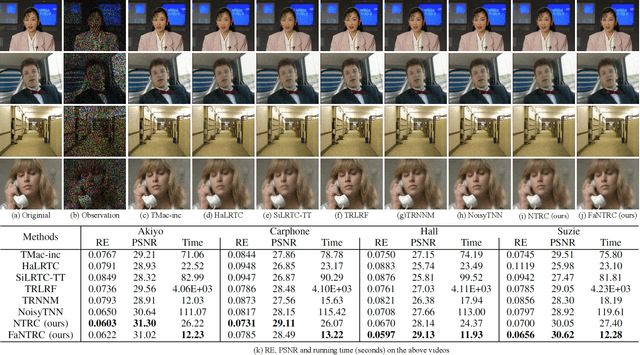
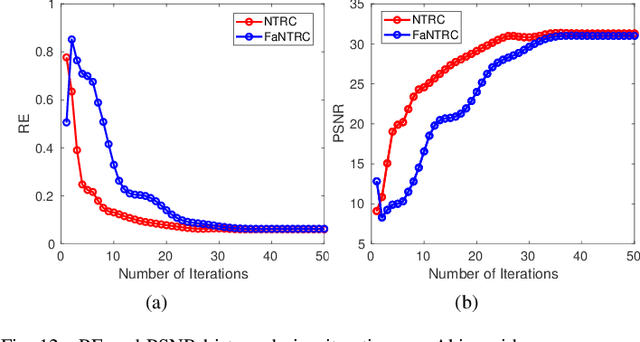
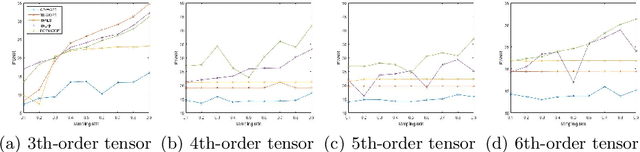
Tensor completion is a fundamental tool for incomplete data analysis, where the goal is to predict missing entries from partial observations. However, existing methods often make the explicit or implicit assumption that the observed entries are noise-free to provide a theoretical guarantee of exact recovery of missing entries, which is quite restrictive in practice. To remedy such drawbacks, this paper proposes a novel noisy tensor completion model, which complements the incompetence of existing works in handling the degeneration of high-order and noisy observations. Specifically, the tensor ring nuclear norm (TRNN) and least-squares estimator are adopted to regularize the underlying tensor and the observed entries, respectively. In addition, a non-asymptotic upper bound of estimation error is provided to depict the statistical performance of the proposed estimator. Two efficient algorithms are developed to solve the optimization problem with convergence guarantee, one of which is specially tailored to handle large-scale tensors by replacing the minimization of TRNN of the original tensor equivalently with that of a much smaller one in a heterogeneous tensor decomposition framework. Experimental results on both synthetic and real-world data demonstrate the effectiveness and efficiency of the proposed model in recovering noisy incomplete tensor data compared with state-of-the-art tensor completion models.