GaussianArt: Unified Modeling of Geometry and Motion for Articulated Objects

Reconstructing articulated objects is essential for building digital twins of interactive environments. However, prior methods typically decouple geometry and motion by first reconstructing object shape in distinct states and then estimating articulation through post-hoc alignment. This separation complicates the reconstruction pipeline and restricts scalability, especially for objects with complex, multi-part articulation. We introduce a unified representation that jointly models geometry and motion using articulated 3D Gaussians. This formulation improves robustness in motion decomposition and supports articulated objects with up to 20 parts, significantly outperforming prior approaches that often struggle beyond 2--3 parts due to brittle initialization. To systematically assess scalability and generalization, we propose MPArt-90, a new benchmark consisting of 90 articulated objects across 20 categories, each with diverse part counts and motion configurations. Extensive experiments show that our method consistently achieves superior accuracy in part-level geometry reconstruction and motion estimation across a broad range of object types. We further demonstrate applicability to downstream tasks such as robotic simulation and human-scene interaction modeling, highlighting the potential of unified articulated representations in scalable physical modeling.

Latent Matrices for Tensor Network Decomposition and to Tensor Completion

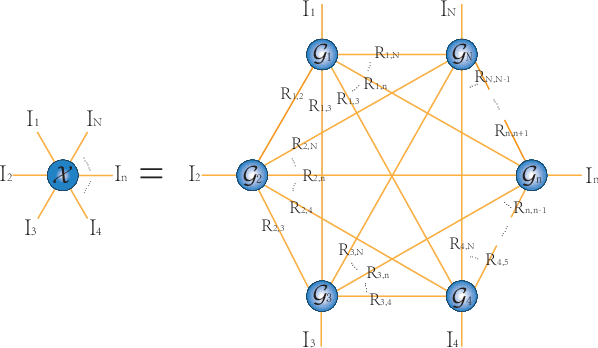
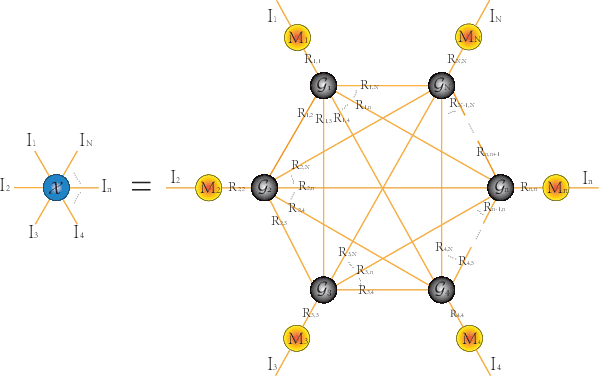
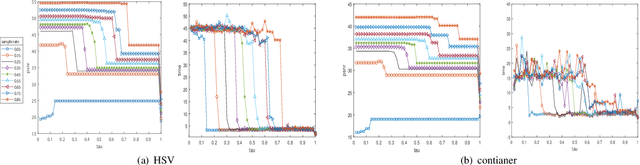
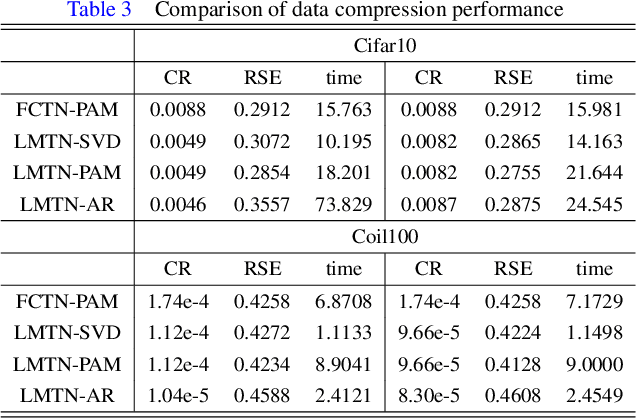
The prevalent fully-connected tensor network (FCTN) has achieved excellent success to compress data. However, the FCTN decomposition suffers from slow computational speed when facing higher-order and large-scale data. Naturally, there arises an interesting question: can a new model be proposed that decomposes the tensor into smaller ones and speeds up the computation of the algorithm? This work gives a positive answer by formulating a novel higher-order tensor decomposition model that utilizes latent matrices based on the tensor network structure, which can decompose a tensor into smaller-scale data than the FCTN decomposition, hence we named it Latent Matrices for Tensor Network Decomposition (LMTN). Furthermore, three optimization algorithms, LMTN-PAM, LMTN-SVD and LMTN-AR, have been developed and applied to the tensor-completion task. In addition, we provide proofs of theoretical convergence and complexity analysis for these algorithms. Experimental results show that our algorithm has the effectiveness in both deep learning dataset compression and higher-order tensor completion, and that our LMTN-SVD algorithm is 3-6 times faster than the FCTN-PAM algorithm and only a 1.8 points accuracy drop.

A high-order tensor completion algorithm based on Fully-Connected Tensor Network weighted optimization

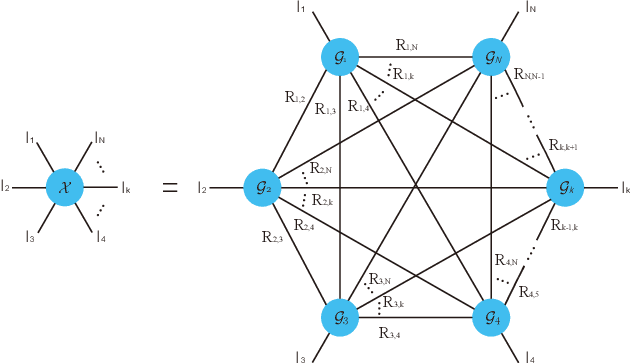
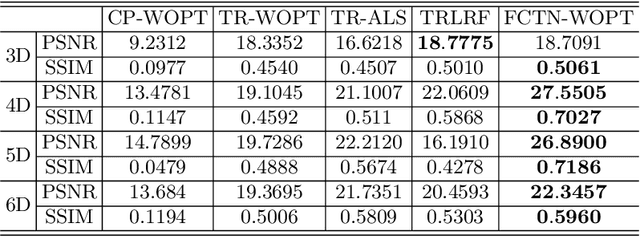
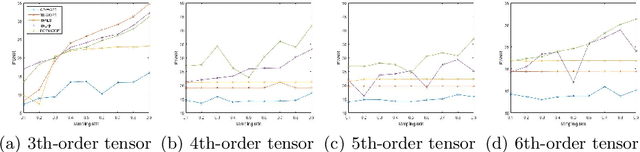
Tensor completion aimes at recovering missing data, and it is one of the popular concerns in deep learning and signal processing. Among the higher-order tensor decomposition algorithms, the recently proposed fully-connected tensor network decomposition (FCTN) algorithm is the most advanced. In this paper, by leveraging the superior expression of the fully-connected tensor network (FCTN) decomposition, we propose a new tensor completion method named the fully connected tensor network weighted optization(FCTN-WOPT). The algorithm performs a composition of the completed tensor by initialising the factors from the FCTN decomposition. We build a loss function with the weight tensor, the completed tensor and the incomplete tensor together, and then update the completed tensor using the lbfgs gradient descent algorithm to reduce the spatial memory occupation and speed up iterations. Finally we test the completion with synthetic data and real data (both image data and video data) and the results show the advanced performance of our FCTN-WOPT when it is applied to higher-order tensor completion.