A high-order tensor completion algorithm based on Fully-Connected Tensor Network weighted optimization

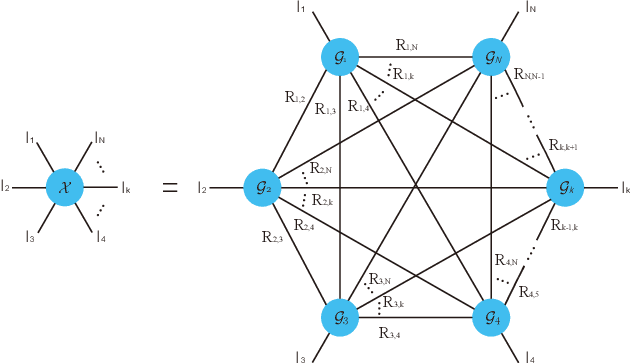
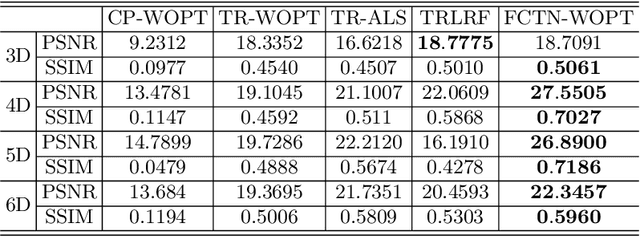
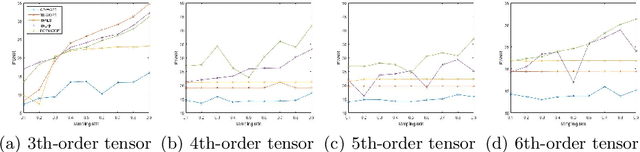
Tensor completion aimes at recovering missing data, and it is one of the popular concerns in deep learning and signal processing. Among the higher-order tensor decomposition algorithms, the recently proposed fully-connected tensor network decomposition (FCTN) algorithm is the most advanced. In this paper, by leveraging the superior expression of the fully-connected tensor network (FCTN) decomposition, we propose a new tensor completion method named the fully connected tensor network weighted optization(FCTN-WOPT). The algorithm performs a composition of the completed tensor by initialising the factors from the FCTN decomposition. We build a loss function with the weight tensor, the completed tensor and the incomplete tensor together, and then update the completed tensor using the lbfgs gradient descent algorithm to reduce the spatial memory occupation and speed up iterations. Finally we test the completion with synthetic data and real data (both image data and video data) and the results show the advanced performance of our FCTN-WOPT when it is applied to higher-order tensor completion.

Driving Anomaly Detection Using Conditional Generative Adversarial Network

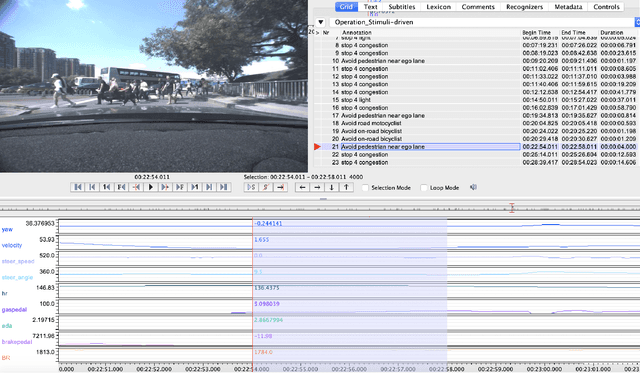
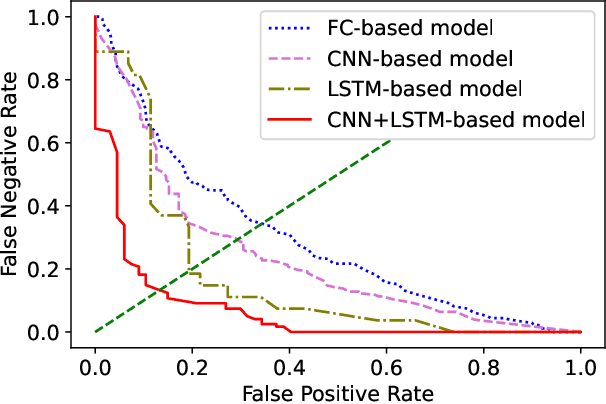
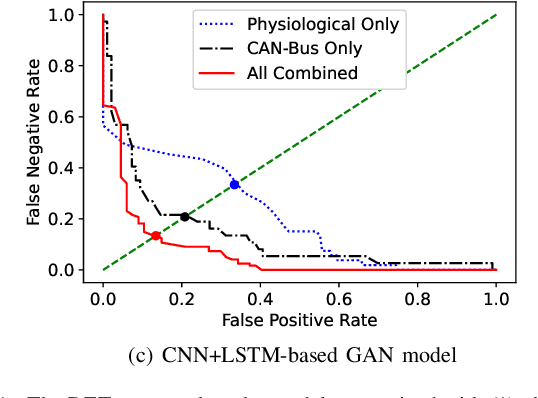
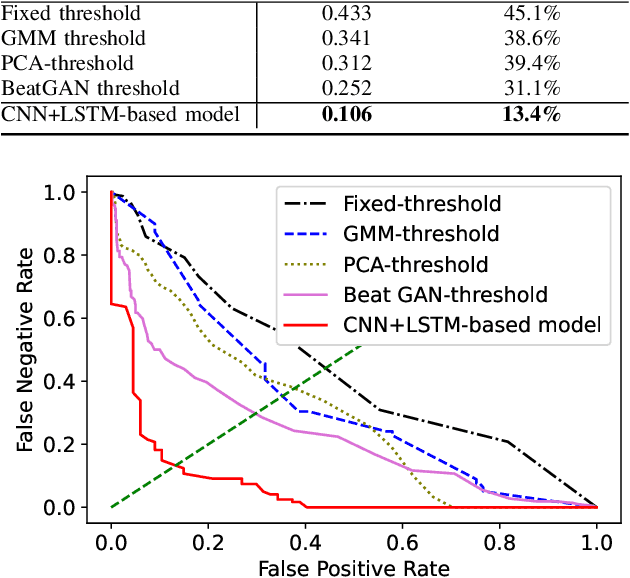
Anomaly driving detection is an important problem in advanced driver assistance systems (ADAS). It is important to identify potential hazard scenarios as early as possible to avoid potential accidents. This study proposes an unsupervised method to quantify driving anomalies using a conditional generative adversarial network (GAN). The approach predicts upcoming driving scenarios by conditioning the models on the previously observed signals. The system uses the difference of the output from the discriminator between the predicted and actual signals as a metric to quantify the anomaly degree of a driving segment. We take a driver-centric approach, considering physiological signals from the driver and controller area network-Bus (CAN-Bus) signals from the vehicle. The approach is implemented with convolutional neural networks (CNNs) to extract discriminative feature representations, and with long short-term memory (LSTM) cells to capture temporal information. The study is implemented and evaluated with the driving anomaly dataset (DAD), which includes 250 hours of naturalistic recordings manually annotated with driving events. The experimental results reveal that recordings annotated with events that are likely to be anomalous, such as avoiding on-road pedestrians and traffic rule violations, have higher anomaly scores than recordings without any event annotation. The results are validated with perceptual evaluations, where annotators are asked to assess the risk and familiarity of the videos detected with high anomaly scores. The results indicate that the driving segments with higher anomaly scores are more risky and less regularly seen on the road than other driving segments, validating the proposed unsupervised approach.

Noisy Tensor Completion via Low-rank Tensor Ring

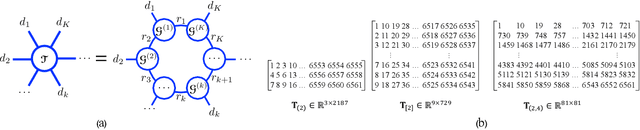
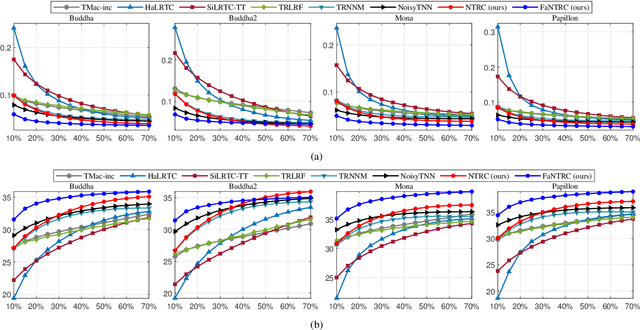
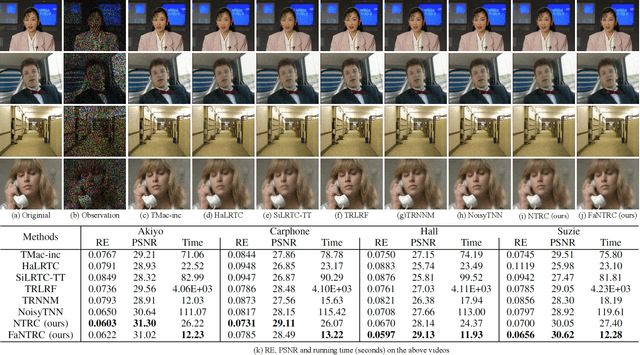
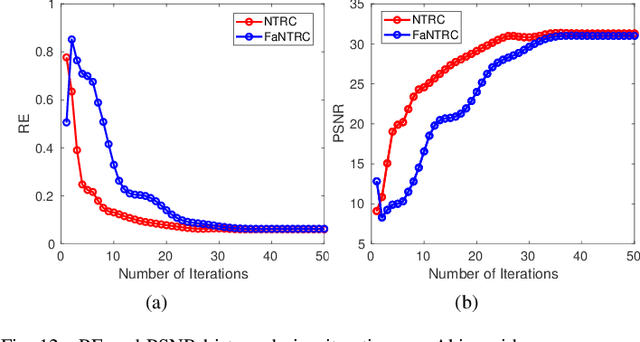
Tensor completion is a fundamental tool for incomplete data analysis, where the goal is to predict missing entries from partial observations. However, existing methods often make the explicit or implicit assumption that the observed entries are noise-free to provide a theoretical guarantee of exact recovery of missing entries, which is quite restrictive in practice. To remedy such drawbacks, this paper proposes a novel noisy tensor completion model, which complements the incompetence of existing works in handling the degeneration of high-order and noisy observations. Specifically, the tensor ring nuclear norm (TRNN) and least-squares estimator are adopted to regularize the underlying tensor and the observed entries, respectively. In addition, a non-asymptotic upper bound of estimation error is provided to depict the statistical performance of the proposed estimator. Two efficient algorithms are developed to solve the optimization problem with convergence guarantee, one of which is specially tailored to handle large-scale tensors by replacing the minimization of TRNN of the original tensor equivalently with that of a much smaller one in a heterogeneous tensor decomposition framework. Experimental results on both synthetic and real-world data demonstrate the effectiveness and efficiency of the proposed model in recovering noisy incomplete tensor data compared with state-of-the-art tensor completion models.

Bayesian Robust Tensor Ring Model for Incomplete Multiway Data

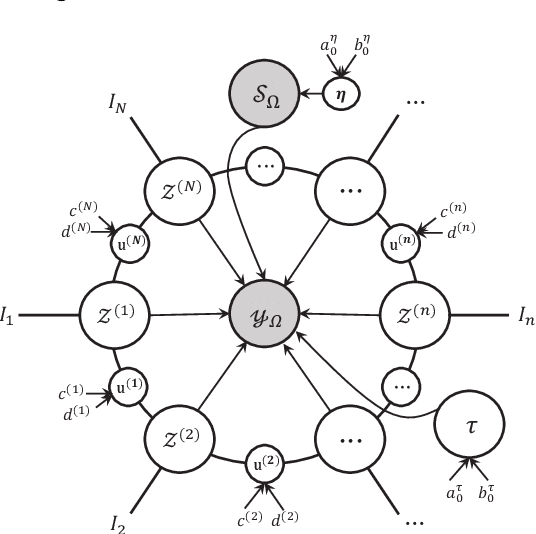
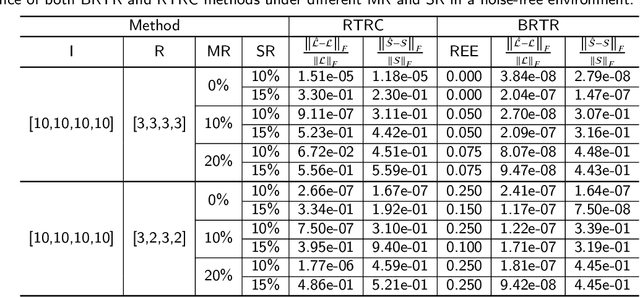
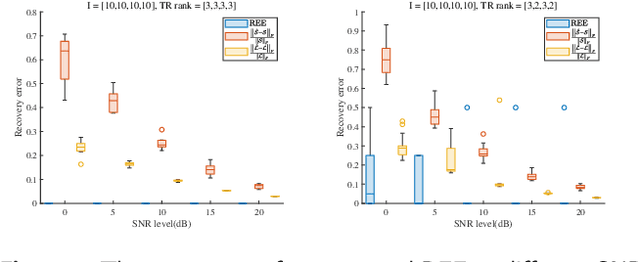
Low-rank tensor completion aims to recover missing entries from the observed data. However, the observed data may be disturbed by noise and outliers. Therefore, robust tensor completion (RTC) is proposed to solve this problem. The recently proposed tensor ring (TR) structure is applied to RTC due to its superior abilities in dealing with high-dimensional data with predesigned TR rank. To avoid manual rank selection and achieve a balance between low-rank component and sparse component, in this paper, we propose a Bayesian robust tensor ring (BRTR) decomposition method for RTC problem. Furthermore, we develop a variational Bayesian (VB) algorithm to infer the probability distribution of posteriors. During the learning process, the frontal slices of previous tensor and horizontal slices of latter tensor shared with the same TR rank with zero components are pruned, resulting in automatic rank determination. Compared with existing methods, BRTR can automatically learn TR rank without manual fine-tuning of parameters. Extensive experiments indicate that BRTR has better recovery performance and ability to remove noise than other state-of-the-art methods.

Efficient Tensor Robust PCA under Hybrid Model of Tucker and Tensor Train

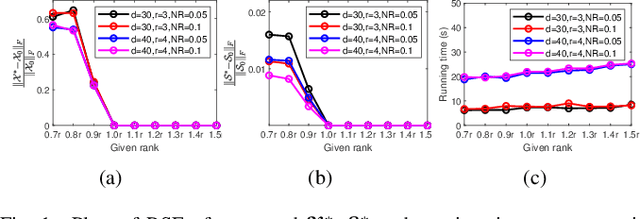
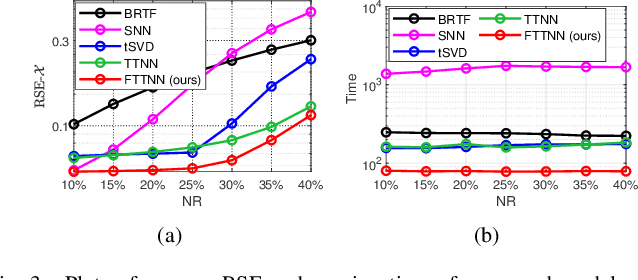
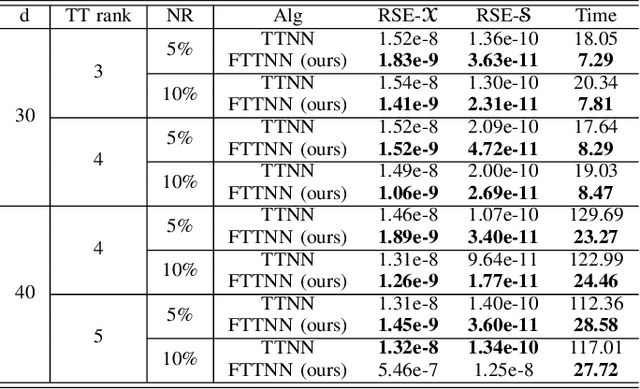
Tensor robust principal component analysis (TRPCA) is a fundamental model in machine learning and computer vision. Recently, tensor train (TT) decomposition has been verified effective to capture the global low-rank correlation for tensor recovery tasks. However, due to the large-scale tensor data in real-world applications, previous TRPCA models often suffer from high computational complexity. In this letter, we propose an efficient TRPCA under hybrid model of Tucker and TT. Specifically, in theory we reveal that TT nuclear norm (TTNN) of the original big tensor can be equivalently converted to that of a much smaller tensor via a Tucker compression format, thereby significantly reducing the computational cost of singular value decomposition (SVD). Numerical experiments on both synthetic and real-world tensor data verify the superiority of the proposed model.

Understanding Convolutional Neural Networks from Theoretical Perspective via Volterra Convolution

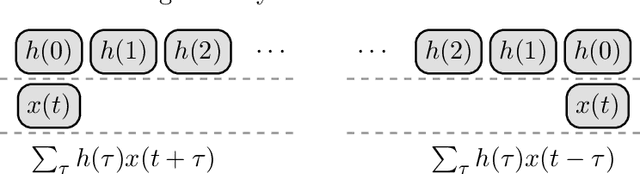
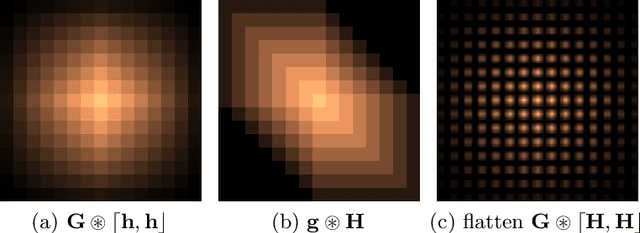
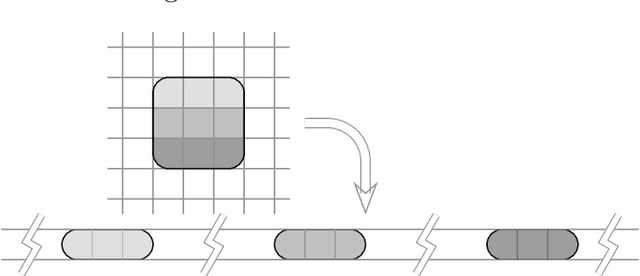
This study proposes a general and unified perspective of convolutional neural networks by exploring the relationship between (deep) convolutional neural networks and finite Volterra convolutions. It provides a novel approach to explain and study the overall characteristics of neural networks without being disturbed by the complex network architectures. Concretely, we examine the basic structures of finite term Volterra convolutions and convolutional neural networks. Our results show that convolutional neural network is an approximation of the finite term Volterra convolution, whose order increases exponentially with the number of layers and kernel size increases exponentially with the strides. With this perspective, the specialized perturbations are directly obtained from the approximated kernels rather than iterative generated adversarial examples. Extensive experiments on synthetic and real-world data sets show the correctness and effectiveness of our results.

An Efficient Tensor Completion Method via New Latent Nuclear Norm

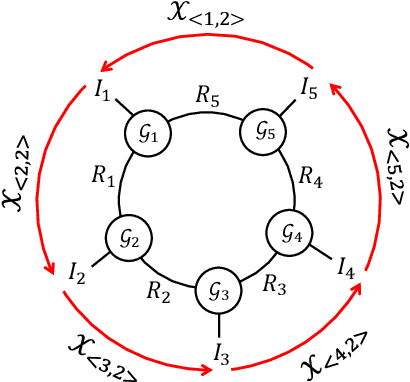
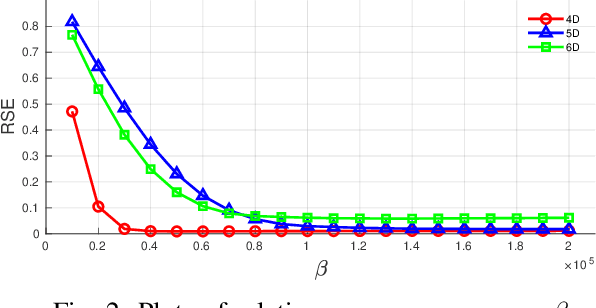
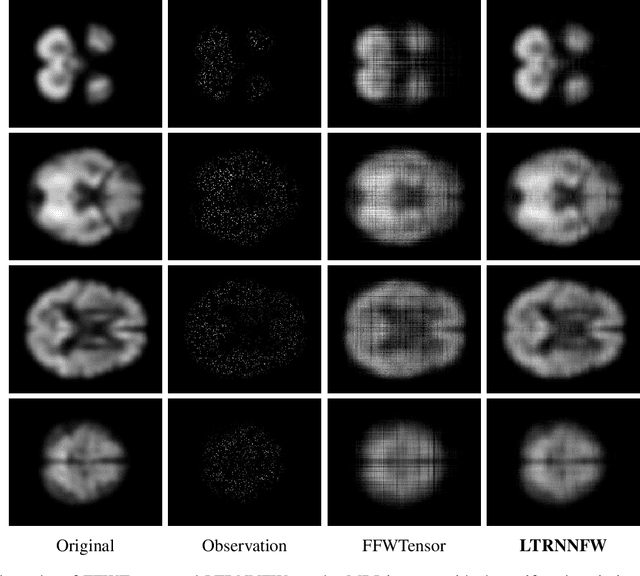
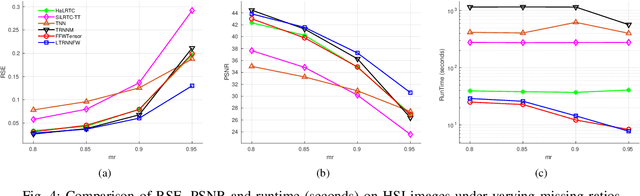
In tensor completion, the latent nuclear norm is commonly used to induce low-rank structure, while substantially failing to capture the global information due to the utilization of unbalanced unfolding scheme. To overcome this drawback, a new latent nuclear norm equipped with a more balanced unfolding scheme is defined for low-rank regularizer. Moreover, the new latent nuclear norm together with the Frank-Wolfe (FW) algorithm is developed as an efficient completion method by utilizing the sparsity structure of observed tensor. Specifically, both FW linear subproblem and line search only need to access the observed entries, by which we can instead maintain the sparse tensors and a set of small basis matrices during iteration. Most operations are based on sparse tensors, and the closed-form solution of FW linear subproblem can be obtained from rank-one SVD. We theoretically analyze the space-complexity and time-complexity of the proposed method, and show that it is much more efficient over other norm-based completion methods for higher-order tensors. Extensive experimental results of visual-data inpainting demonstrate that the proposed method is able to achieve state-of-the-art performance at smaller costs of time and space, which is very meaningful for the memory-limited equipment in practical applications.

Deep Approximately Orthogonal Nonnegative Matrix Factorization for Clustering

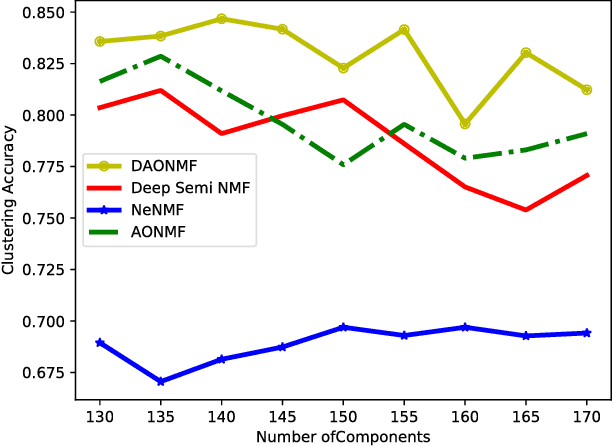
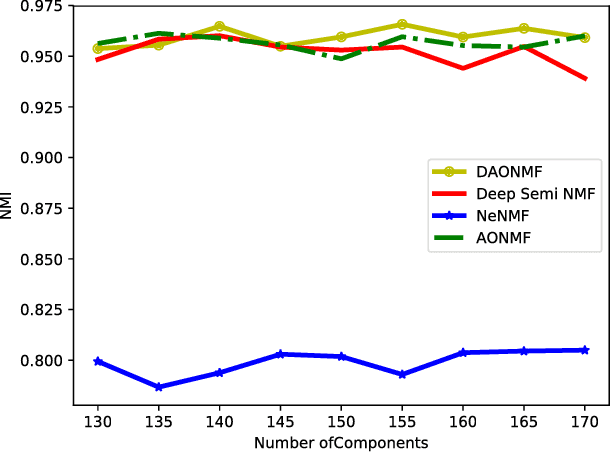
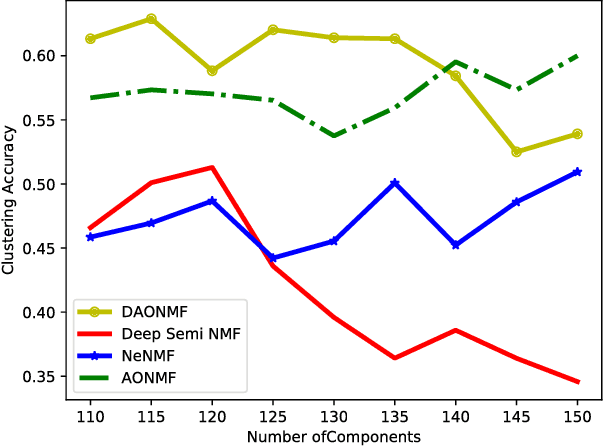
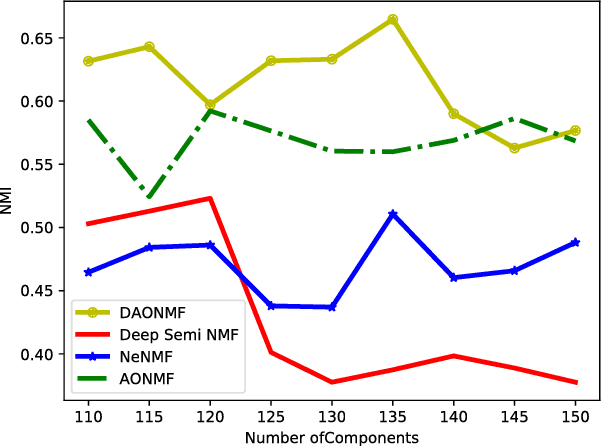
Nonnegative Matrix Factorization (NMF) is a widely used technique for data representation. Inspired by the expressive power of deep learning, several NMF variants equipped with deep architectures have been proposed. However, these methods mostly use the only nonnegativity while ignoring task-specific features of data. In this paper, we propose a novel deep approximately orthogonal nonnegative matrix factorization method where both nonnegativity and orthogonality are imposed with the aim to perform a hierarchical clustering by using different level of abstractions of data. Experiment on two face image datasets showed that the proposed method achieved better clustering performance than other deep matrix factorization methods and state-of-the-art single layer NMF variants.