Spiking Graph Neural Network on Riemannian Manifolds

Graph neural networks (GNNs) have become the dominant solution for learning on graphs, the typical non-Euclidean structures. Conventional GNNs, constructed with the Artificial Neuron Network (ANN), have achieved impressive performance at the cost of high computation and energy consumption. In parallel, spiking GNNs with brain-like spiking neurons are drawing increasing research attention owing to the energy efficiency. So far, existing spiking GNNs consider graphs in Euclidean space, ignoring the structural geometry, and suffer from the high latency issue due to Back-Propagation-Through-Time (BPTT) with the surrogate gradient. In light of the aforementioned issues, we are devoted to exploring spiking GNN on Riemannian manifolds, and present a Manifold-valued Spiking GNN (MSG). In particular, we design a new spiking neuron on geodesically complete manifolds with the diffeomorphism, so that BPTT regarding the spikes is replaced by the proposed differentiation via manifold. Theoretically, we show that MSG approximates a solver of the manifold ordinary differential equation. Extensive experiments on common graphs show the proposed MSG achieves superior performance to previous spiking GNNs and energy efficiency to conventional GNNs.

LSEnet: Lorentz Structural Entropy Neural Network for Deep Graph Clustering

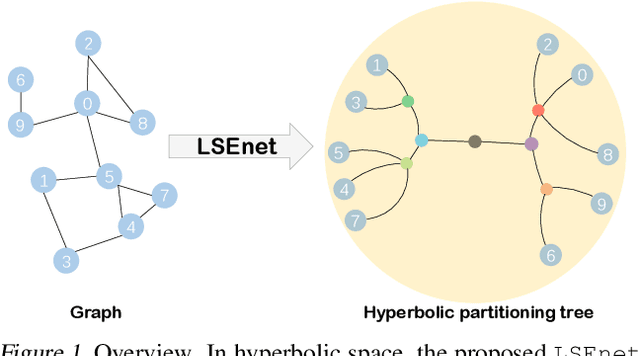
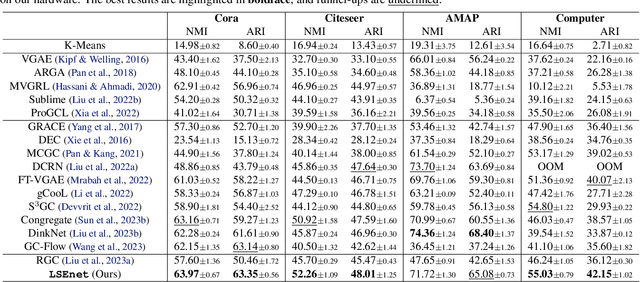
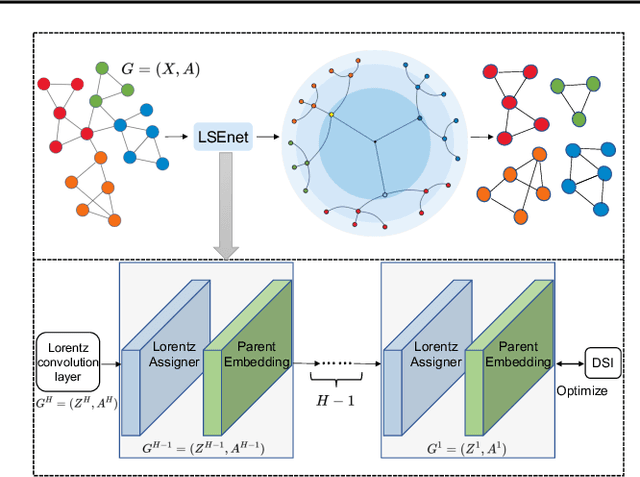
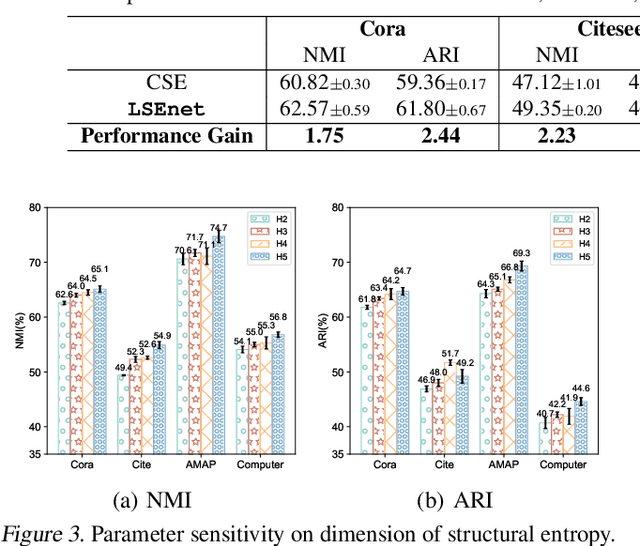
Graph clustering is a fundamental problem in machine learning. Deep learning methods achieve the state-of-the-art results in recent years, but they still cannot work without predefined cluster numbers. Such limitation motivates us to pose a more challenging problem of graph clustering with unknown cluster number. We propose to address this problem from a fresh perspective of graph information theory (i.e., structural information). In the literature, structural information has not yet been introduced to deep clustering, and its classic definition falls short of discrete formulation and modeling node features. In this work, we first formulate a differentiable structural information (DSI) in the continuous realm, accompanied by several theoretical results. By minimizing DSI, we construct the optimal partitioning tree where densely connected nodes in the graph tend to have the same assignment, revealing the cluster structure. DSI is also theoretically presented as a new graph clustering objective, not requiring the predefined cluster number. Furthermore, we design a neural LSEnet in the Lorentz model of hyperbolic space, where we integrate node features to structural information via manifold-valued graph convolution. Extensive empirical results on real graphs show the superiority of our approach.

DeepRicci: Self-supervised Graph Structure-Feature Co-Refinement for Alleviating Over-squashing

Graph Neural Networks (GNNs) have shown great power for learning and mining on graphs, and Graph Structure Learning (GSL) plays an important role in boosting GNNs with a refined graph. In the literature, most GSL solutions either primarily focus on structure refinement with task-specific supervision (i.e., node classification), or overlook the inherent weakness of GNNs themselves (e.g., over-squashing), resulting in suboptimal performance despite sophisticated designs. In light of these limitations, we propose to study self-supervised graph structure-feature co-refinement for effectively alleviating the issue of over-squashing in typical GNNs. In this paper, we take a fundamentally different perspective of the Ricci curvature in Riemannian geometry, in which we encounter the challenges of modeling, utilizing and computing Ricci curvature. To tackle these challenges, we present a self-supervised Riemannian model, DeepRicci. Specifically, we introduce a latent Riemannian space of heterogeneous curvatures to model various Ricci curvatures, and propose a gyrovector feature mapping to utilize Ricci curvature for typical GNNs. Thereafter, we refine node features by geometric contrastive learning among different geometric views, and simultaneously refine graph structure by backward Ricci flow based on a novel formulation of differentiable Ricci curvature. Finally, extensive experiments on public datasets show the superiority of DeepRicci, and the connection between backward Ricci flow and over-squashing. Codes of our work are given in https://github.com/RiemanGraph/.

Motif-aware Riemannian Graph Neural Network with Generative-Contrastive Learning

Graphs are typical non-Euclidean data of complex structures. In recent years, Riemannian graph representation learning has emerged as an exciting alternative to Euclidean ones. However, Riemannian methods are still in an early stage: most of them present a single curvature (radius) regardless of structural complexity, suffer from numerical instability due to the exponential/logarithmic map, and lack the ability to capture motif regularity. In light of the issues above, we propose the problem of \emph{Motif-aware Riemannian Graph Representation Learning}, seeking a numerically stable encoder to capture motif regularity in a diverse-curvature manifold without labels. To this end, we present a novel Motif-aware Riemannian model with Generative-Contrastive learning (MotifRGC), which conducts a minmax game in Riemannian manifold in a self-supervised manner. First, we propose a new type of Riemannian GCN (D-GCN), in which we construct a diverse-curvature manifold by a product layer with the diversified factor, and replace the exponential/logarithmic map by a stable kernel layer. Second, we introduce a motif-aware Riemannian generative-contrastive learning to capture motif regularity in the constructed manifold and learn motif-aware node representation without external labels. Empirical results show the superiority of MofitRGC.

Bayesian Robust Tensor Ring Model for Incomplete Multiway Data

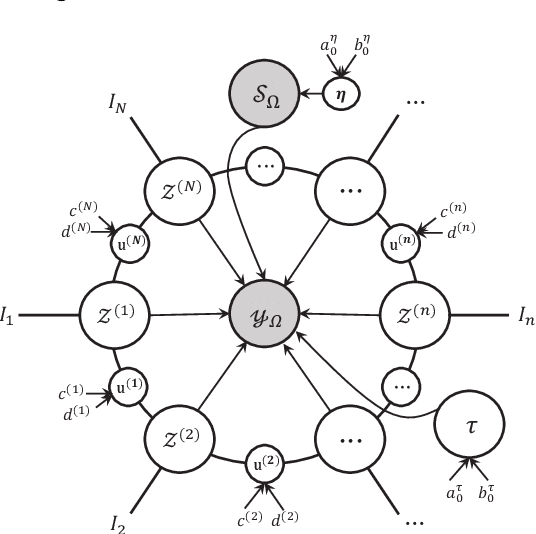
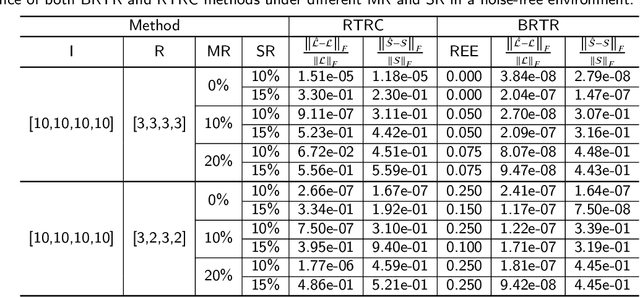
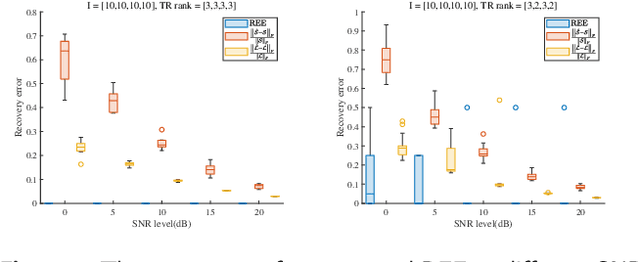
Low-rank tensor completion aims to recover missing entries from the observed data. However, the observed data may be disturbed by noise and outliers. Therefore, robust tensor completion (RTC) is proposed to solve this problem. The recently proposed tensor ring (TR) structure is applied to RTC due to its superior abilities in dealing with high-dimensional data with predesigned TR rank. To avoid manual rank selection and achieve a balance between low-rank component and sparse component, in this paper, we propose a Bayesian robust tensor ring (BRTR) decomposition method for RTC problem. Furthermore, we develop a variational Bayesian (VB) algorithm to infer the probability distribution of posteriors. During the learning process, the frontal slices of previous tensor and horizontal slices of latter tensor shared with the same TR rank with zero components are pruned, resulting in automatic rank determination. Compared with existing methods, BRTR can automatically learn TR rank without manual fine-tuning of parameters. Extensive experiments indicate that BRTR has better recovery performance and ability to remove noise than other state-of-the-art methods.

Efficient Tensor Robust PCA under Hybrid Model of Tucker and Tensor Train

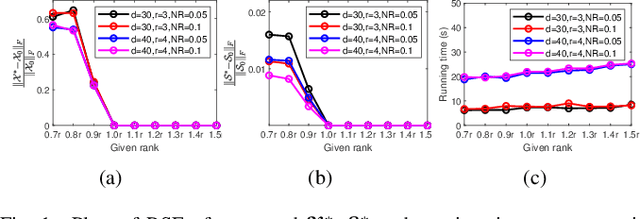
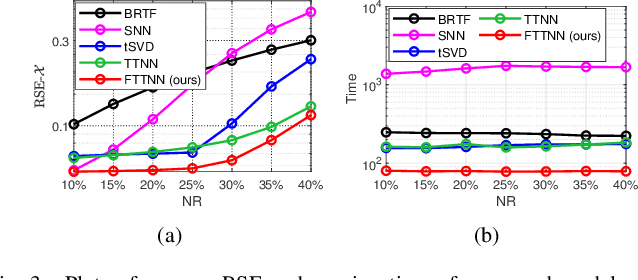
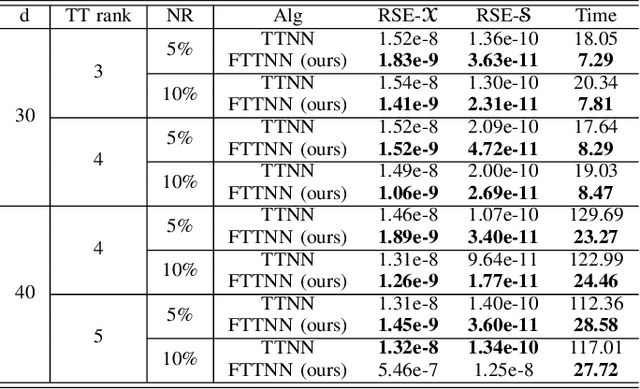
Tensor robust principal component analysis (TRPCA) is a fundamental model in machine learning and computer vision. Recently, tensor train (TT) decomposition has been verified effective to capture the global low-rank correlation for tensor recovery tasks. However, due to the large-scale tensor data in real-world applications, previous TRPCA models often suffer from high computational complexity. In this letter, we propose an efficient TRPCA under hybrid model of Tucker and TT. Specifically, in theory we reveal that TT nuclear norm (TTNN) of the original big tensor can be equivalently converted to that of a much smaller tensor via a Tucker compression format, thereby significantly reducing the computational cost of singular value decomposition (SVD). Numerical experiments on both synthetic and real-world tensor data verify the superiority of the proposed model.