Spiking Graph Neural Network on Riemannian Manifolds
Paper and Code
Oct 23, 2024


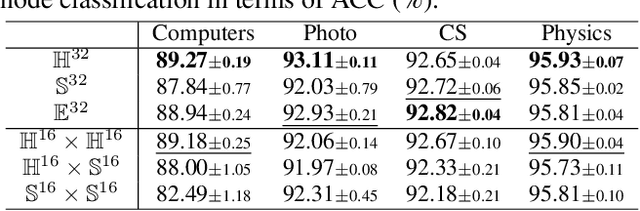
Graph neural networks (GNNs) have become the dominant solution for learning on graphs, the typical non-Euclidean structures. Conventional GNNs, constructed with the Artificial Neuron Network (ANN), have achieved impressive performance at the cost of high computation and energy consumption. In parallel, spiking GNNs with brain-like spiking neurons are drawing increasing research attention owing to the energy efficiency. So far, existing spiking GNNs consider graphs in Euclidean space, ignoring the structural geometry, and suffer from the high latency issue due to Back-Propagation-Through-Time (BPTT) with the surrogate gradient. In light of the aforementioned issues, we are devoted to exploring spiking GNN on Riemannian manifolds, and present a Manifold-valued Spiking GNN (MSG). In particular, we design a new spiking neuron on geodesically complete manifolds with the diffeomorphism, so that BPTT regarding the spikes is replaced by the proposed differentiation via manifold. Theoretically, we show that MSG approximates a solver of the manifold ordinary differential equation. Extensive experiments on common graphs show the proposed MSG achieves superior performance to previous spiking GNNs and energy efficiency to conventional GNNs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge