DeepRicci: Self-supervised Graph Structure-Feature Co-Refinement for Alleviating Over-squashing

Graph Neural Networks (GNNs) have shown great power for learning and mining on graphs, and Graph Structure Learning (GSL) plays an important role in boosting GNNs with a refined graph. In the literature, most GSL solutions either primarily focus on structure refinement with task-specific supervision (i.e., node classification), or overlook the inherent weakness of GNNs themselves (e.g., over-squashing), resulting in suboptimal performance despite sophisticated designs. In light of these limitations, we propose to study self-supervised graph structure-feature co-refinement for effectively alleviating the issue of over-squashing in typical GNNs. In this paper, we take a fundamentally different perspective of the Ricci curvature in Riemannian geometry, in which we encounter the challenges of modeling, utilizing and computing Ricci curvature. To tackle these challenges, we present a self-supervised Riemannian model, DeepRicci. Specifically, we introduce a latent Riemannian space of heterogeneous curvatures to model various Ricci curvatures, and propose a gyrovector feature mapping to utilize Ricci curvature for typical GNNs. Thereafter, we refine node features by geometric contrastive learning among different geometric views, and simultaneously refine graph structure by backward Ricci flow based on a novel formulation of differentiable Ricci curvature. Finally, extensive experiments on public datasets show the superiority of DeepRicci, and the connection between backward Ricci flow and over-squashing. Codes of our work are given in https://github.com/RiemanGraph/.

Contrastive Sequential Interaction Network Learning on Co-Evolving Riemannian Spaces

The sequential interaction network usually find itself in a variety of applications, e.g., recommender system. Herein, inferring future interaction is of fundamental importance, and previous efforts are mainly focused on the dynamics in the classic zero-curvature Euclidean space. Despite the promising results achieved by previous methods, a range of significant issues still largely remains open: On the bipartite nature, is it appropriate to place user and item nodes in one identical space regardless of their inherent difference? On the network dynamics, instead of a fixed curvature space, will the representation spaces evolve when new interactions arrive continuously? On the learning paradigm, can we get rid of the label information costly to acquire? To address the aforementioned issues, we propose a novel Contrastive model for Sequential Interaction Network learning on Co-Evolving RiEmannian spaces, CSINCERE. To the best of our knowledge, we are the first to introduce a couple of co-evolving representation spaces, rather than a single or static space, and propose a co-contrastive learning for the sequential interaction network. In CSINCERE, we formulate a Cross-Space Aggregation for message-passing across representation spaces of different Riemannian geometries, and design a Neural Curvature Estimator based on Ricci curvatures for modeling the space evolvement over time. Thereafter, we present a Reweighed Co-Contrast between the temporal views of the sequential network, so that the couple of Riemannian spaces interact with each other for the interaction prediction without labels. Empirical results on 5 public datasets show the superiority of CSINCERE over the state-of-the-art methods.

SINCERE: Sequential Interaction Networks representation learning on Co-Evolving RiEmannian manifolds

Sequential interaction networks (SIN) have been commonly adopted in many applications such as recommendation systems, search engines and social networks to describe the mutual influence between users and items/products. Efforts on representing SIN are mainly focused on capturing the dynamics of networks in Euclidean space, and recently plenty of work has extended to hyperbolic geometry for implicit hierarchical learning. Previous approaches which learn the embedding trajectories of users and items achieve promising results. However, there are still a range of fundamental issues remaining open. For example, is it appropriate to place user and item nodes in one identical space regardless of their inherent discrepancy? Instead of residing in a single fixed curvature space, how will the representation spaces evolve when new interaction occurs? To explore these issues for sequential interaction networks, we propose SINCERE, a novel method representing Sequential Interaction Networks on Co-Evolving RiEmannian manifolds. SIN- CERE not only takes the user and item embedding trajectories in respective spaces into account, but also emphasizes on the space evolvement that how curvature changes over time. Specifically, we introduce a fresh cross-geometry aggregation which allows us to propagate information across different Riemannian manifolds without breaking conformal invariance, and a curvature estimator which is delicately designed to predict global curvatures effectively according to current local Ricci curvatures. Extensive experiments on several real-world datasets demonstrate the promising performance of SINCERE over the state-of-the-art sequential interaction prediction methods.

Contrastive Graph Clustering in Curvature Spaces

Graph clustering is a longstanding research topic, and has achieved remarkable success with the deep learning methods in recent years. Nevertheless, we observe that several important issues largely remain open. On the one hand, graph clustering from the geometric perspective is appealing but has rarely been touched before, as it lacks a promising space for geometric clustering. On the other hand, contrastive learning boosts the deep graph clustering but usually struggles in either graph augmentation or hard sample mining. To bridge this gap, we rethink the problem of graph clustering from geometric perspective and, to the best of our knowledge, make the first attempt to introduce a heterogeneous curvature space to graph clustering problem. Correspondingly, we present a novel end-to-end contrastive graph clustering model named CONGREGATE, addressing geometric graph clustering with Ricci curvatures. To support geometric clustering, we construct a theoretically grounded Heterogeneous Curvature Space where deep representations are generated via the product of the proposed fully Riemannian graph convolutional nets. Thereafter, we train the graph clusters by an augmentation-free reweighted contrastive approach where we pay more attention to both hard negatives and hard positives in our curvature space. Empirical results on real-world graphs show that our model outperforms the state-of-the-art competitors.

Self-Supervised Continual Graph Learning in Adaptive Riemannian Spaces

Continual graph learning routinely finds its role in a variety of real-world applications where the graph data with different tasks come sequentially. Despite the success of prior works, it still faces great challenges. On the one hand, existing methods work with the zero-curvature Euclidean space, and largely ignore the fact that curvature varies over the coming graph sequence. On the other hand, continual learners in the literature rely on abundant labels, but labeling graph in practice is particularly hard especially for the continuously emerging graphs on-the-fly. To address the aforementioned challenges, we propose to explore a challenging yet practical problem, the self-supervised continual graph learning in adaptive Riemannian spaces. In this paper, we propose a novel self-supervised Riemannian Graph Continual Learner (RieGrace). In RieGrace, we first design an Adaptive Riemannian GCN (AdaRGCN), a unified GCN coupled with a neural curvature adapter, so that Riemannian space is shaped by the learnt curvature adaptive to each graph. Then, we present a Label-free Lorentz Distillation approach, in which we create teacher-student AdaRGCN for the graph sequence. The student successively performs intra-distillation from itself and inter-distillation from the teacher so as to consolidate knowledge without catastrophic forgetting. In particular, we propose a theoretically grounded Generalized Lorentz Projection for the contrastive distillation in Riemannian space. Extensive experiments on the benchmark datasets show the superiority of RieGrace, and additionally, we investigate on how curvature changes over the graph sequence.

A Self-supervised Riemannian GNN with Time Varying Curvature for Temporal Graph Learning

Representation learning on temporal graphs has drawn considerable research attention owing to its fundamental importance in a wide spectrum of real-world applications. Though a number of studies succeed in obtaining time-dependent representations, it still faces significant challenges. On the one hand, most of the existing methods restrict the embedding space with a certain curvature. However, the underlying geometry in fact shifts among the positive curvature hyperspherical, zero curvature Euclidean and negative curvature hyperbolic spaces in the evolvement over time. On the other hand, these methods usually require abundant labels to learn temporal representations, and thereby notably limit their wide use in the unlabeled graphs of the real applications. To bridge this gap, we make the first attempt to study the problem of self-supervised temporal graph representation learning in the general Riemannian space, supporting the time-varying curvature to shift among hyperspherical, Euclidean and hyperbolic spaces. In this paper, we present a novel self-supervised Riemannian graph neural network (SelfRGNN). Specifically, we design a curvature-varying Riemannian GNN with a theoretically grounded time encoding, and formulate a functional curvature over time to model the evolvement shifting among the positive, zero and negative curvature spaces. To enable the self-supervised learning, we propose a novel reweighting self-contrastive approach, exploring the Riemannian space itself without augmentation, and propose an edge-based self-supervised curvature learning with the Ricci curvature. Extensive experiments show the superiority of SelfRGNN, and moreover, the case study shows the time-varying curvature of temporal graph in reality.

A Self-supervised Mixed-curvature Graph Neural Network

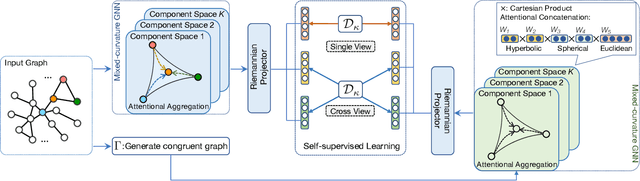
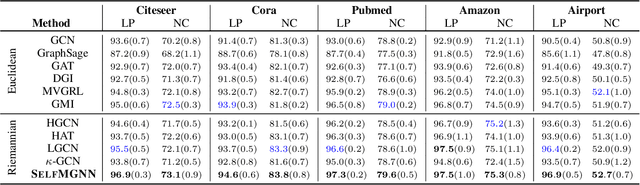
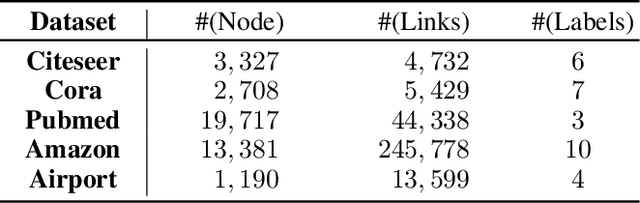
Graph representation learning received increasing attentions in recent years. Most of existing methods ignore the complexity of the graph structures and restrict graphs in a single constant-curvature representation space, which is only suitable to particular kinds of graph structure indeed. Additionally, these methods follow the supervised or semi-supervised learning paradigm, and thereby notably limit their deployment on the unlabeled graphs in real applications. To address these aforementioned limitations, we take the first attempt to study the self-supervised graph representation learning in the mixed-curvature spaces. In this paper, we present a novel Self-supervised Mixed-curvature Graph Neural Network (SelfMGNN). Instead of working on one single constant-curvature space, we construct a mixed-curvature space via the Cartesian product of multiple Riemannian component spaces and design hierarchical attention mechanisms for learning and fusing the representations across these component spaces. To enable the self-supervisd learning, we propose a novel dual contrastive approach. The mixed-curvature Riemannian space actually provides multiple Riemannian views for the contrastive learning. We introduce a Riemannian projector to reveal these views, and utilize a well-designed Riemannian discriminator for the single-view and cross-view contrastive learning within and across the Riemannian views. Finally, extensive experiments show that SelfMGNN captures the complicated graph structures in reality and outperforms state-of-the-art baselines.