BitCoin: Bidirectional Tagging and Supervised Contrastive Learning based Joint Relational Triple Extraction Framework

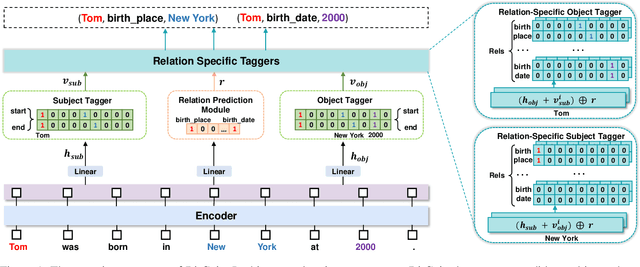
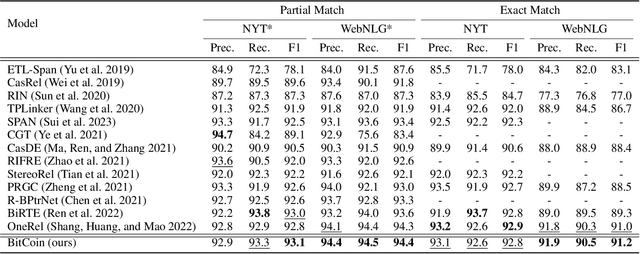
Relation triple extraction (RTE) is an essential task in information extraction and knowledge graph construction. Despite recent advancements, existing methods still exhibit certain limitations. They just employ generalized pre-trained models and do not consider the specificity of RTE tasks. Moreover, existing tagging-based approaches typically decompose the RTE task into two subtasks, initially identifying subjects and subsequently identifying objects and relations. They solely focus on extracting relational triples from subject to object, neglecting that once the extraction of a subject fails, it fails in extracting all triples associated with that subject. To address these issues, we propose BitCoin, an innovative Bidirectional tagging and supervised Contrastive learning based joint relational triple extraction framework. Specifically, we design a supervised contrastive learning method that considers multiple positives per anchor rather than restricting it to just one positive. Furthermore, a penalty term is introduced to prevent excessive similarity between the subject and object. Our framework implements taggers in two directions, enabling triples extraction from subject to object and object to subject. Experimental results show that BitCoin achieves state-of-the-art results on the benchmark datasets and significantly improves the F1 score on Normal, SEO, EPO, and multiple relation extraction tasks.

SINCERE: Sequential Interaction Networks representation learning on Co-Evolving RiEmannian manifolds

Sequential interaction networks (SIN) have been commonly adopted in many applications such as recommendation systems, search engines and social networks to describe the mutual influence between users and items/products. Efforts on representing SIN are mainly focused on capturing the dynamics of networks in Euclidean space, and recently plenty of work has extended to hyperbolic geometry for implicit hierarchical learning. Previous approaches which learn the embedding trajectories of users and items achieve promising results. However, there are still a range of fundamental issues remaining open. For example, is it appropriate to place user and item nodes in one identical space regardless of their inherent discrepancy? Instead of residing in a single fixed curvature space, how will the representation spaces evolve when new interaction occurs? To explore these issues for sequential interaction networks, we propose SINCERE, a novel method representing Sequential Interaction Networks on Co-Evolving RiEmannian manifolds. SIN- CERE not only takes the user and item embedding trajectories in respective spaces into account, but also emphasizes on the space evolvement that how curvature changes over time. Specifically, we introduce a fresh cross-geometry aggregation which allows us to propagate information across different Riemannian manifolds without breaking conformal invariance, and a curvature estimator which is delicately designed to predict global curvatures effectively according to current local Ricci curvatures. Extensive experiments on several real-world datasets demonstrate the promising performance of SINCERE over the state-of-the-art sequential interaction prediction methods.

A Self-supervised Mixed-curvature Graph Neural Network

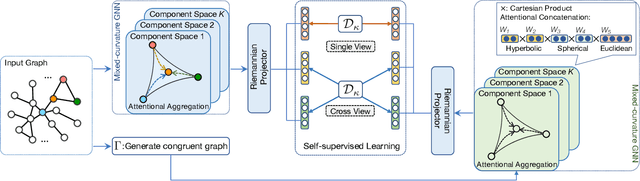
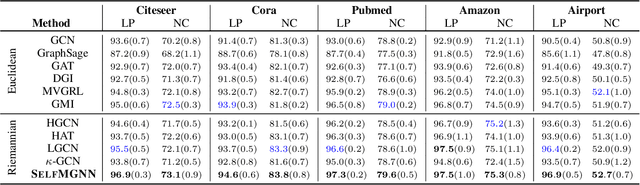
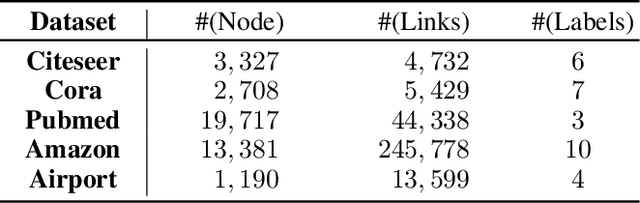
Graph representation learning received increasing attentions in recent years. Most of existing methods ignore the complexity of the graph structures and restrict graphs in a single constant-curvature representation space, which is only suitable to particular kinds of graph structure indeed. Additionally, these methods follow the supervised or semi-supervised learning paradigm, and thereby notably limit their deployment on the unlabeled graphs in real applications. To address these aforementioned limitations, we take the first attempt to study the self-supervised graph representation learning in the mixed-curvature spaces. In this paper, we present a novel Self-supervised Mixed-curvature Graph Neural Network (SelfMGNN). Instead of working on one single constant-curvature space, we construct a mixed-curvature space via the Cartesian product of multiple Riemannian component spaces and design hierarchical attention mechanisms for learning and fusing the representations across these component spaces. To enable the self-supervisd learning, we propose a novel dual contrastive approach. The mixed-curvature Riemannian space actually provides multiple Riemannian views for the contrastive learning. We introduce a Riemannian projector to reveal these views, and utilize a well-designed Riemannian discriminator for the single-view and cross-view contrastive learning within and across the Riemannian views. Finally, extensive experiments show that SelfMGNN captures the complicated graph structures in reality and outperforms state-of-the-art baselines.

Hyperbolic Variational Graph Neural Network for Modeling Dynamic Graphs

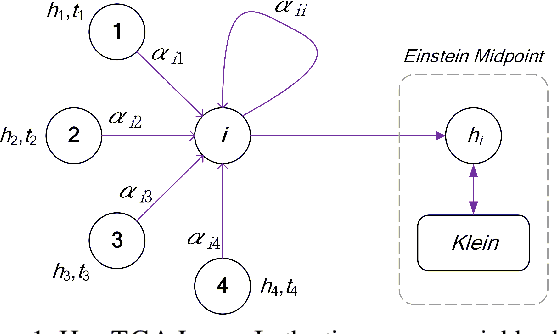
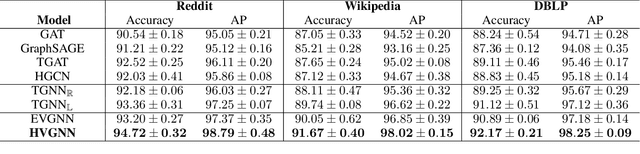
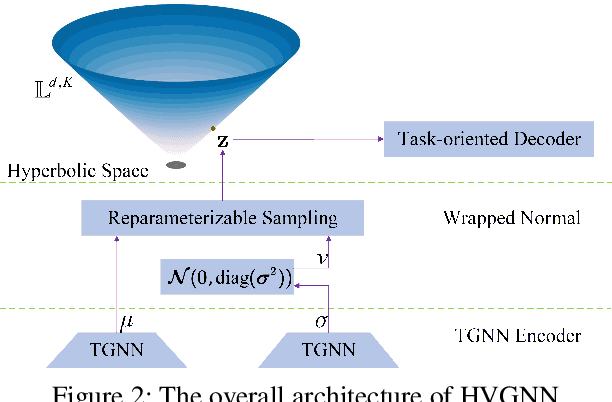
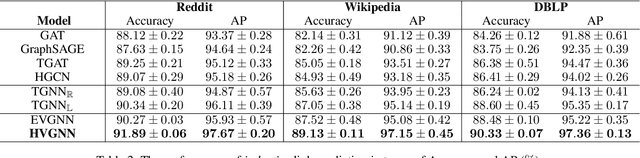
Learning representations for graphs plays a critical role in a wide spectrum of downstream applications. In this paper, we summarize the limitations of the prior works in three folds: representation space, modeling dynamics and modeling uncertainty. To bridge this gap, we propose to learn dynamic graph representation in hyperbolic space, for the first time, which aims to infer stochastic node representations. Working with hyperbolic space, we present a novel Hyperbolic Variational Graph Neural Network, referred to as HVGNN. In particular, to model the dynamics, we introduce a Temporal GNN (TGNN) based on a theoretically grounded time encoding approach. To model the uncertainty, we devise a hyperbolic graph variational autoencoder built upon the proposed TGNN to generate stochastic node representations of hyperbolic normal distributions. Furthermore, we introduce a reparameterisable sampling algorithm for the hyperbolic normal distribution to enable the gradient-based learning of HVGNN. Extensive experiments show that HVGNN outperforms state-of-the-art baselines on real-world datasets.