A Self-supervised Mixed-curvature Graph Neural Network
Paper and Code
Dec 10, 2021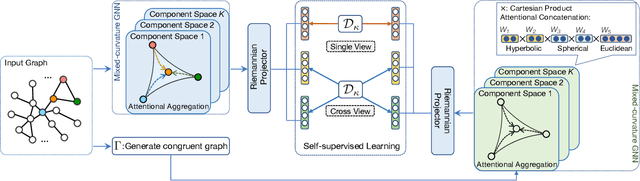

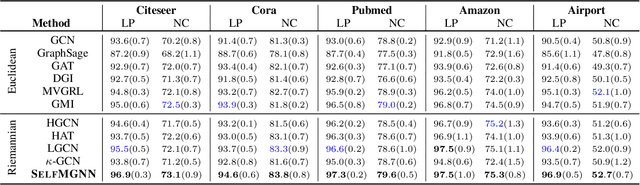
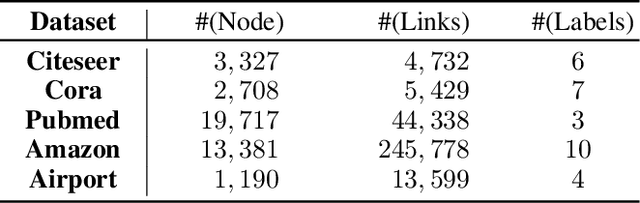
Graph representation learning received increasing attentions in recent years. Most of existing methods ignore the complexity of the graph structures and restrict graphs in a single constant-curvature representation space, which is only suitable to particular kinds of graph structure indeed. Additionally, these methods follow the supervised or semi-supervised learning paradigm, and thereby notably limit their deployment on the unlabeled graphs in real applications. To address these aforementioned limitations, we take the first attempt to study the self-supervised graph representation learning in the mixed-curvature spaces. In this paper, we present a novel Self-supervised Mixed-curvature Graph Neural Network (SelfMGNN). Instead of working on one single constant-curvature space, we construct a mixed-curvature space via the Cartesian product of multiple Riemannian component spaces and design hierarchical attention mechanisms for learning and fusing the representations across these component spaces. To enable the self-supervisd learning, we propose a novel dual contrastive approach. The mixed-curvature Riemannian space actually provides multiple Riemannian views for the contrastive learning. We introduce a Riemannian projector to reveal these views, and utilize a well-designed Riemannian discriminator for the single-view and cross-view contrastive learning within and across the Riemannian views. Finally, extensive experiments show that SelfMGNN captures the complicated graph structures in reality and outperforms state-of-the-art baselines.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge