LSEnet: Lorentz Structural Entropy Neural Network for Deep Graph Clustering
Paper and Code
May 20, 2024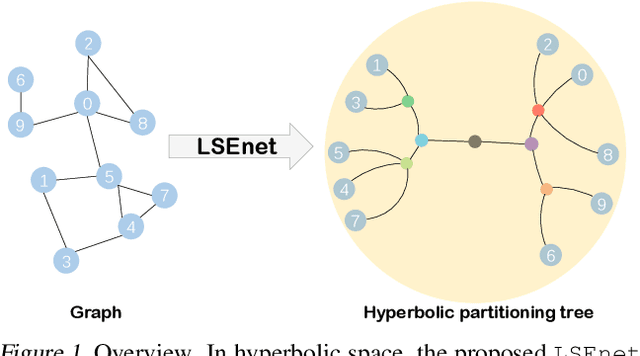
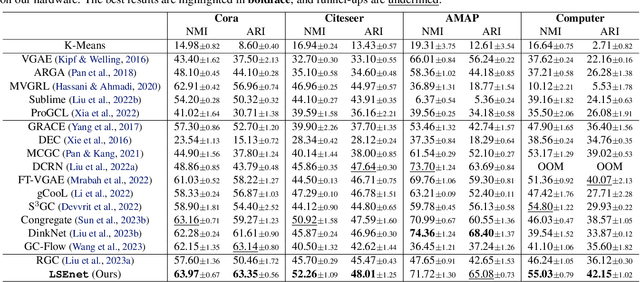
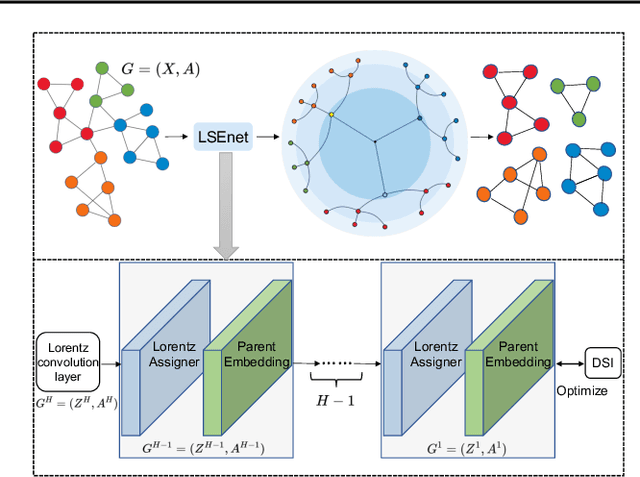
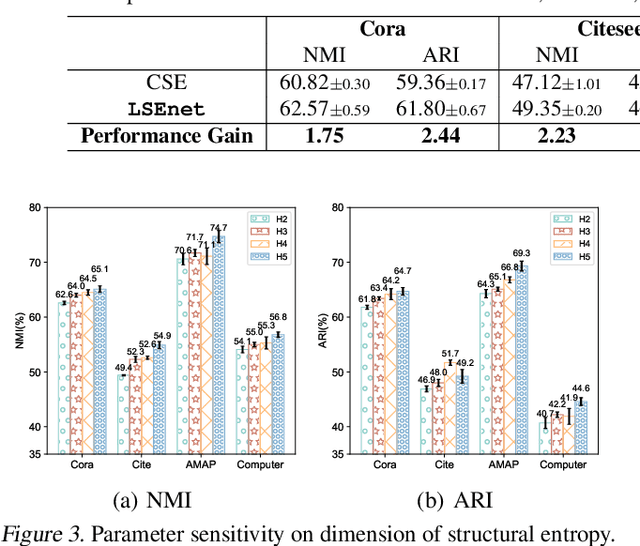
Graph clustering is a fundamental problem in machine learning. Deep learning methods achieve the state-of-the-art results in recent years, but they still cannot work without predefined cluster numbers. Such limitation motivates us to pose a more challenging problem of graph clustering with unknown cluster number. We propose to address this problem from a fresh perspective of graph information theory (i.e., structural information). In the literature, structural information has not yet been introduced to deep clustering, and its classic definition falls short of discrete formulation and modeling node features. In this work, we first formulate a differentiable structural information (DSI) in the continuous realm, accompanied by several theoretical results. By minimizing DSI, we construct the optimal partitioning tree where densely connected nodes in the graph tend to have the same assignment, revealing the cluster structure. DSI is also theoretically presented as a new graph clustering objective, not requiring the predefined cluster number. Furthermore, we design a neural LSEnet in the Lorentz model of hyperbolic space, where we integrate node features to structural information via manifold-valued graph convolution. Extensive empirical results on real graphs show the superiority of our approach.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge