Bayesian Robust Tensor Ring Model for Incomplete Multiway Data

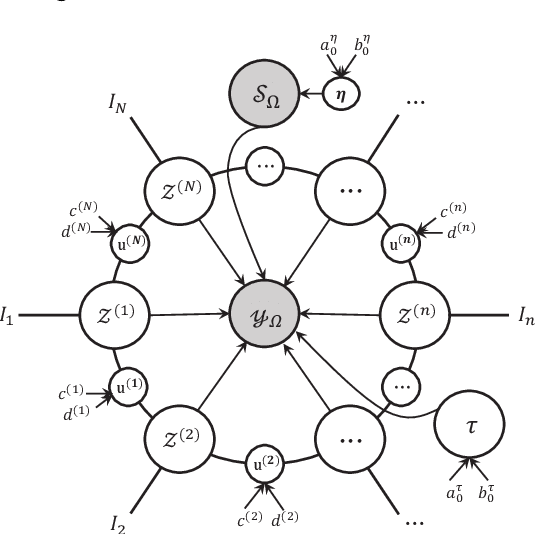
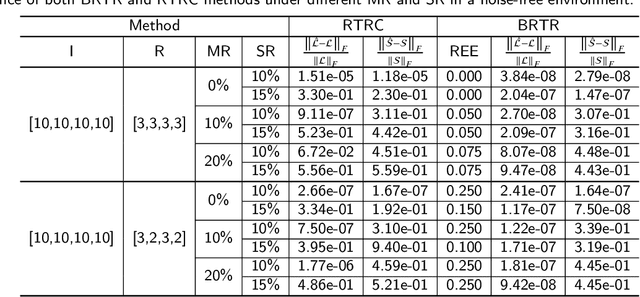
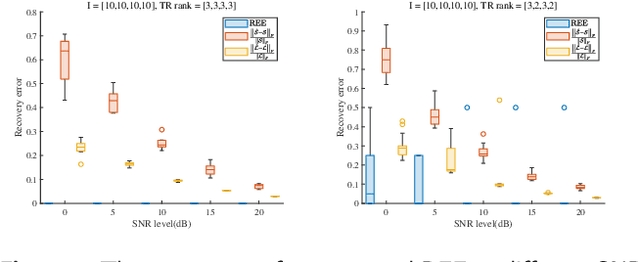
Low-rank tensor completion aims to recover missing entries from the observed data. However, the observed data may be disturbed by noise and outliers. Therefore, robust tensor completion (RTC) is proposed to solve this problem. The recently proposed tensor ring (TR) structure is applied to RTC due to its superior abilities in dealing with high-dimensional data with predesigned TR rank. To avoid manual rank selection and achieve a balance between low-rank component and sparse component, in this paper, we propose a Bayesian robust tensor ring (BRTR) decomposition method for RTC problem. Furthermore, we develop a variational Bayesian (VB) algorithm to infer the probability distribution of posteriors. During the learning process, the frontal slices of previous tensor and horizontal slices of latter tensor shared with the same TR rank with zero components are pruned, resulting in automatic rank determination. Compared with existing methods, BRTR can automatically learn TR rank without manual fine-tuning of parameters. Extensive experiments indicate that BRTR has better recovery performance and ability to remove noise than other state-of-the-art methods.