An Efficient Tensor Completion Method via New Latent Nuclear Norm

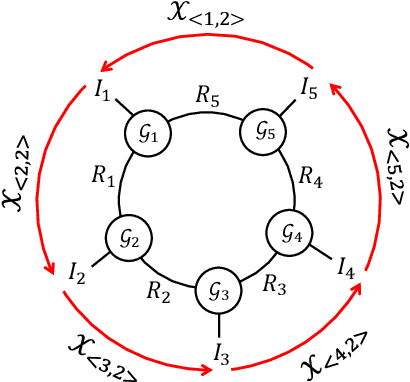
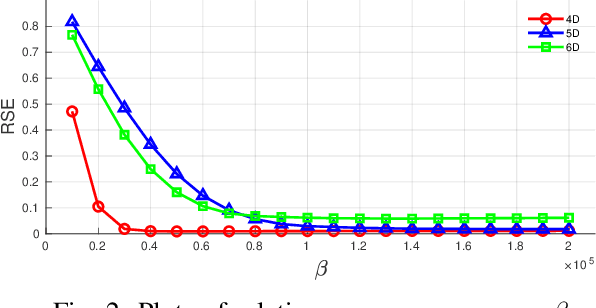
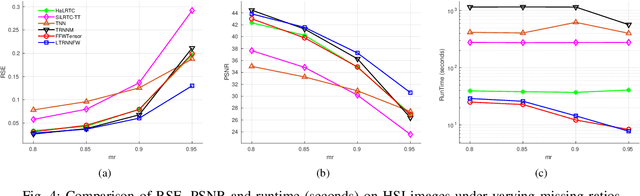
In tensor completion, the latent nuclear norm is commonly used to induce low-rank structure, while substantially failing to capture the global information due to the utilization of unbalanced unfolding scheme. To overcome this drawback, a new latent nuclear norm equipped with a more balanced unfolding scheme is defined for low-rank regularizer. Moreover, the new latent nuclear norm together with the Frank-Wolfe (FW) algorithm is developed as an efficient completion method by utilizing the sparsity structure of observed tensor. Specifically, both FW linear subproblem and line search only need to access the observed entries, by which we can instead maintain the sparse tensors and a set of small basis matrices during iteration. Most operations are based on sparse tensors, and the closed-form solution of FW linear subproblem can be obtained from rank-one SVD. We theoretically analyze the space-complexity and time-complexity of the proposed method, and show that it is much more efficient over other norm-based completion methods for higher-order tensors. Extensive experimental results of visual-data inpainting demonstrate that the proposed method is able to achieve state-of-the-art performance at smaller costs of time and space, which is very meaningful for the memory-limited equipment in practical applications.

Tensor-Ring Nuclear Norm Minimization and Application for Visual Data Completion

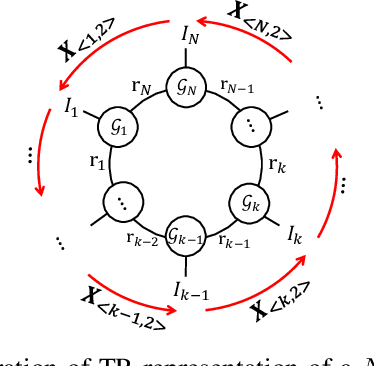
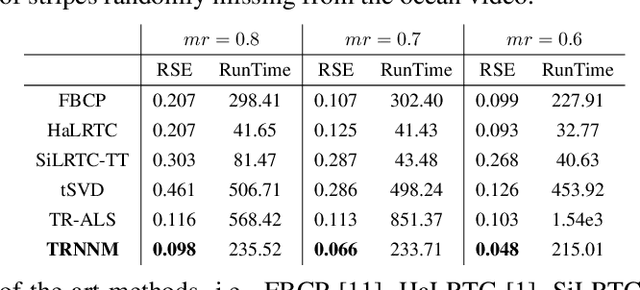
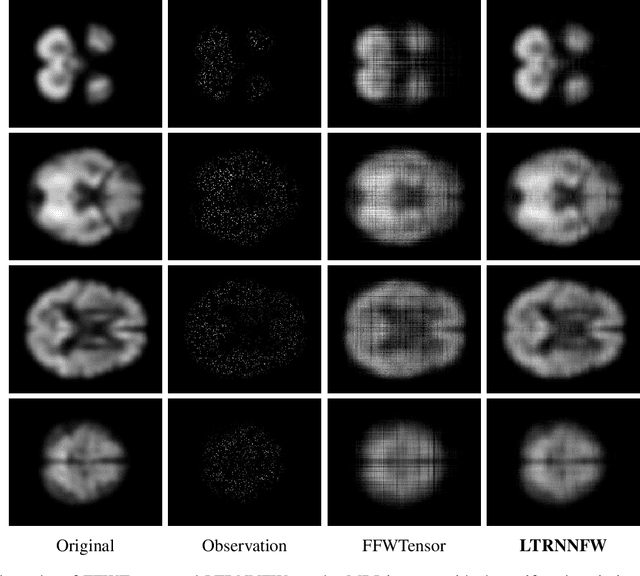
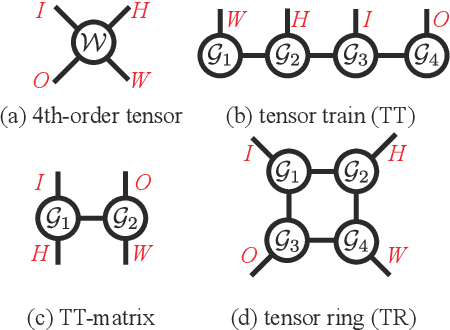
Tensor ring (TR) decomposition has been successfully used to obtain the state-of-the-art performance in the visual data completion problem. However, the existing TR-based completion methods are severely non-convex and computationally demanding. In addition, the determination of the optimal TR rank is a tough work in practice. To overcome these drawbacks, we first introduce a class of new tensor nuclear norms by using tensor circular unfolding. Then we theoretically establish connection between the rank of the circularly-unfolded matrices and the TR ranks. We also develop an efficient tensor completion algorithm by minimizing the proposed tensor nuclear norm. Extensive experimental results demonstrate that our proposed tensor completion method outperforms the conventional tensor completion methods in the image/video in-painting problem with striped missing values.

Low-Rank Embedding of Kernels in Convolutional Neural Networks under Random Shuffling

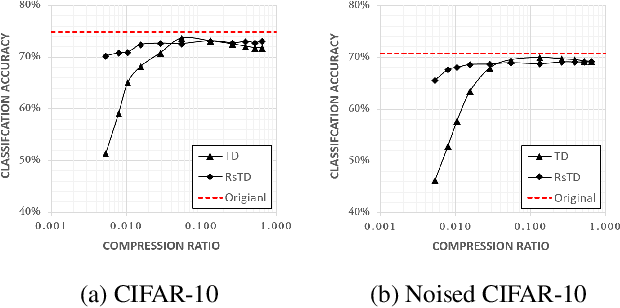
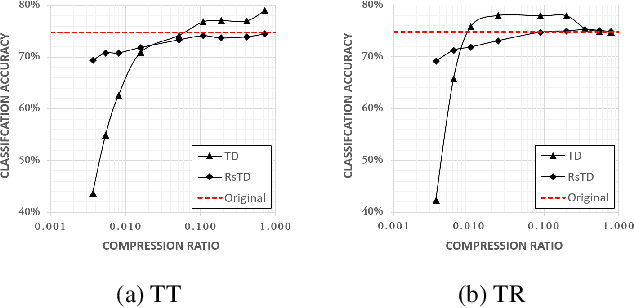
Although the convolutional neural networks (CNNs) have become popular for various image processing and computer vision task recently, it remains a challenging problem to reduce the storage cost of the parameters for resource-limited platforms. In the previous studies, tensor decomposition (TD) has achieved promising compression performance by embedding the kernel of a convolutional layer into a low-rank subspace. However the employment of TD is naively on the kernel or its specified variants. Unlike the conventional approaches, this paper shows that the kernel can be embedded into more general or even random low-rank subspaces. We demonstrate this by compressing the convolutional layers via randomly-shuffled tensor decomposition (RsTD) for a standard classification task using CIFAR-10. In addition, we analyze how the spatial similarity of the training data influences the low-rank structure of the kernels. The experimental results show that the CNN can be significantly compressed even if the kernels are randomly shuffled. Furthermore, the RsTD-based method yields more stable classification accuracy than the conventional TD-based methods in a large range of compression ratios.

Learning the Hierarchical Parts of Objects by Deep Non-Smooth Nonnegative Matrix Factorization

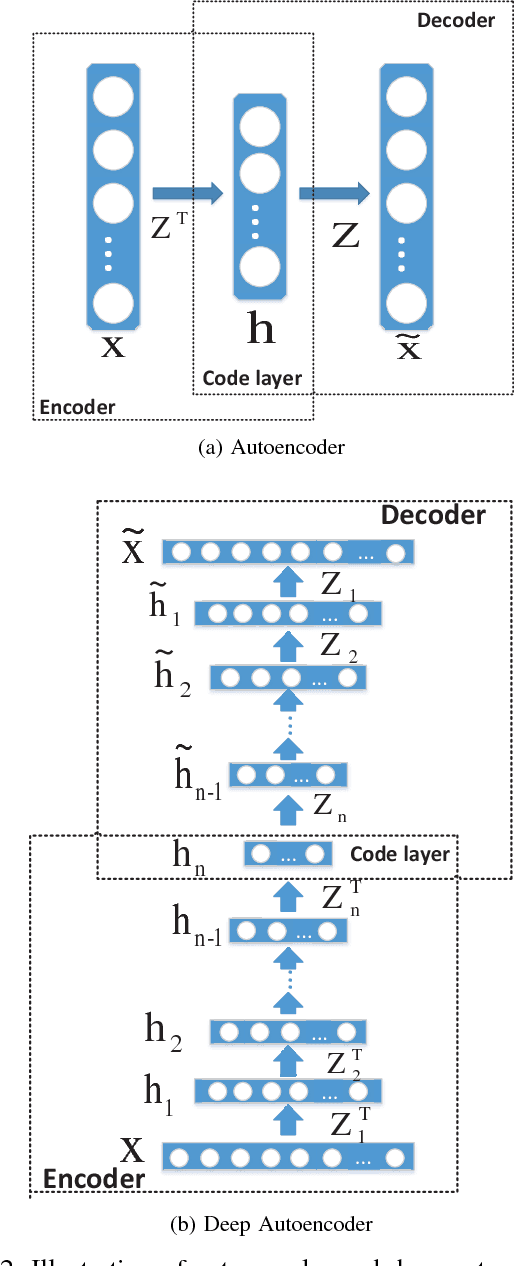
Nonsmooth Nonnegative Matrix Factorization (nsNMF) is capable of producing more localized, less overlapped feature representations than other variants of NMF while keeping satisfactory fit to data. However, nsNMF as well as other existing NMF methods is incompetent to learn hierarchical features of complex data due to its shallow structure. To fill this gap, we propose a deep nsNMF method coined by the fact that it possesses a deeper architecture compared with standard nsNMF. The deep nsNMF not only gives parts-based features due to the nonnegativity constraints, but also creates higher-level, more abstract features by combing lower-level ones. The in-depth description of how deep architecture can help to efficiently discover abstract features in dnsNMF is presented. And we also show that the deep nsNMF has close relationship with the deep autoencoder, suggesting that the proposed model inherits the major advantages from both deep learning and NMF. Extensive experiments demonstrate the standout performance of the proposed method in clustering analysis.