Prompt-based Grouping Transformer for Nucleus Detection and Classification

Automatic nuclei detection and classification can produce effective information for disease diagnosis. Most existing methods classify nuclei independently or do not make full use of the semantic similarity between nuclei and their grouping features. In this paper, we propose a novel end-to-end nuclei detection and classification framework based on a grouping transformer-based classifier. The nuclei classifier learns and updates the representations of nuclei groups and categories via hierarchically grouping the nucleus embeddings. Then the cell types are predicted with the pairwise correlations between categorical embeddings and nucleus features. For the efficiency of the fully transformer-based framework, we take the nucleus group embeddings as the input prompts of backbone, which helps harvest grouping guided features by tuning only the prompts instead of the whole backbone. Experimental results show that the proposed method significantly outperforms the existing models on three datasets.

Towards Efficient and Accurate Approximation: Tensor Decomposition Based on Randomized Block Krylov Iteration

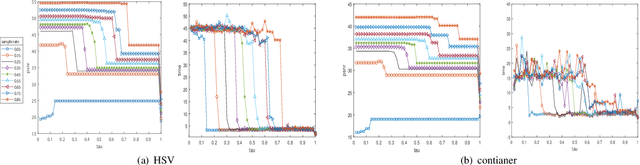
Efficient and accurate low-rank approximation (LRA) methods are of great significance for large-scale data analysis. Randomized tensor decompositions have emerged as powerful tools to meet this need, but most existing methods perform poorly in the presence of noise interference. Inspired by the remarkable performance of randomized block Krylov iteration (rBKI) in reducing the effect of tail singular values, this work designs an rBKI-based Tucker decomposition (rBKI-TK) for accurate approximation, together with a hierarchical tensor ring decomposition based on rBKI-TK for efficient compression of large-scale data. Besides, the error bound between the deterministic LRA and the randomized LRA is studied. Numerical experiences demonstrate the efficiency, accuracy and scalability of the proposed methods in both data compression and denoising.

Latent Matrices for Tensor Network Decomposition and to Tensor Completion

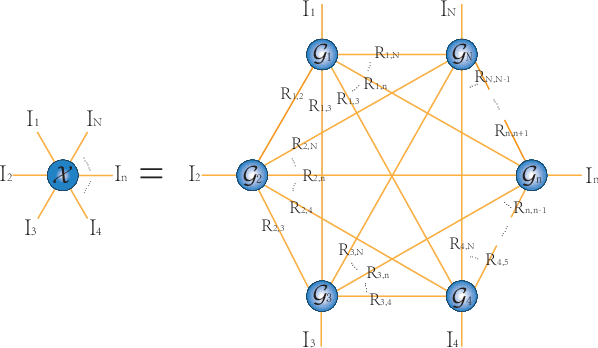
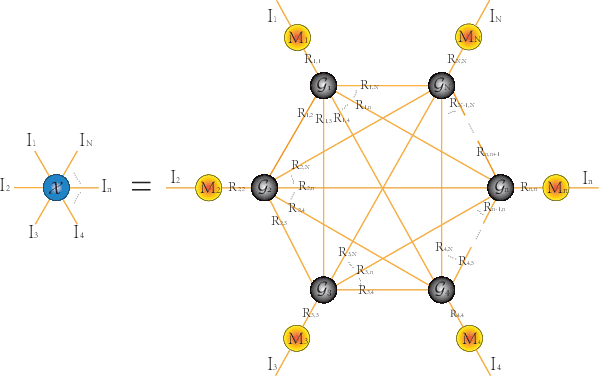
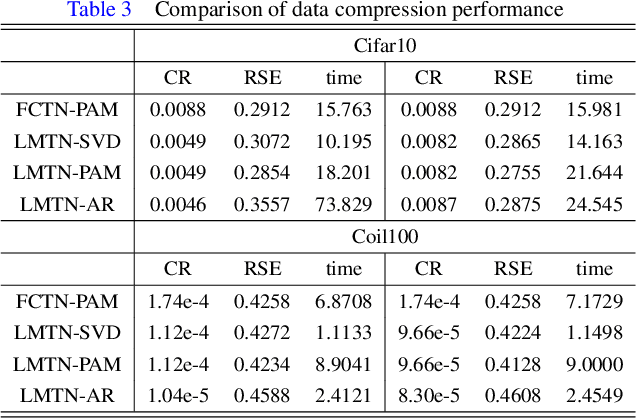
The prevalent fully-connected tensor network (FCTN) has achieved excellent success to compress data. However, the FCTN decomposition suffers from slow computational speed when facing higher-order and large-scale data. Naturally, there arises an interesting question: can a new model be proposed that decomposes the tensor into smaller ones and speeds up the computation of the algorithm? This work gives a positive answer by formulating a novel higher-order tensor decomposition model that utilizes latent matrices based on the tensor network structure, which can decompose a tensor into smaller-scale data than the FCTN decomposition, hence we named it Latent Matrices for Tensor Network Decomposition (LMTN). Furthermore, three optimization algorithms, LMTN-PAM, LMTN-SVD and LMTN-AR, have been developed and applied to the tensor-completion task. In addition, we provide proofs of theoretical convergence and complexity analysis for these algorithms. Experimental results show that our algorithm has the effectiveness in both deep learning dataset compression and higher-order tensor completion, and that our LMTN-SVD algorithm is 3-6 times faster than the FCTN-PAM algorithm and only a 1.8 points accuracy drop.

A high-order tensor completion algorithm based on Fully-Connected Tensor Network weighted optimization

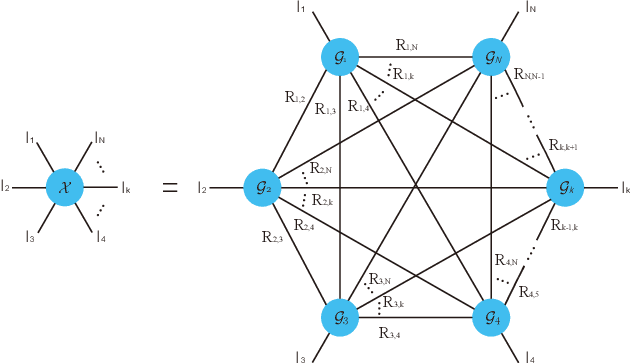
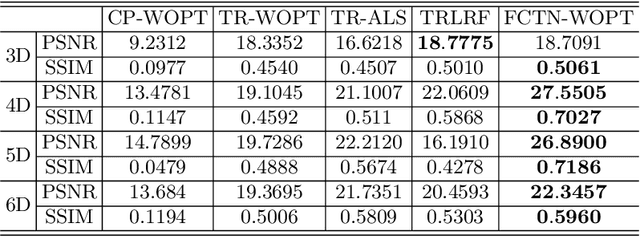
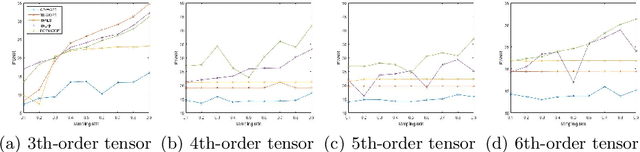
Tensor completion aimes at recovering missing data, and it is one of the popular concerns in deep learning and signal processing. Among the higher-order tensor decomposition algorithms, the recently proposed fully-connected tensor network decomposition (FCTN) algorithm is the most advanced. In this paper, by leveraging the superior expression of the fully-connected tensor network (FCTN) decomposition, we propose a new tensor completion method named the fully connected tensor network weighted optization(FCTN-WOPT). The algorithm performs a composition of the completed tensor by initialising the factors from the FCTN decomposition. We build a loss function with the weight tensor, the completed tensor and the incomplete tensor together, and then update the completed tensor using the lbfgs gradient descent algorithm to reduce the spatial memory occupation and speed up iterations. Finally we test the completion with synthetic data and real data (both image data and video data) and the results show the advanced performance of our FCTN-WOPT when it is applied to higher-order tensor completion.

Fast Hypergraph Regularized Nonnegative Tensor Ring Factorization Based on Low-Rank Approximation

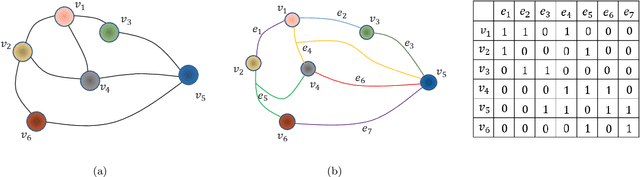
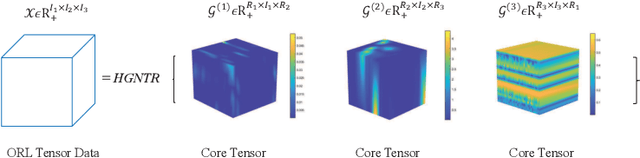
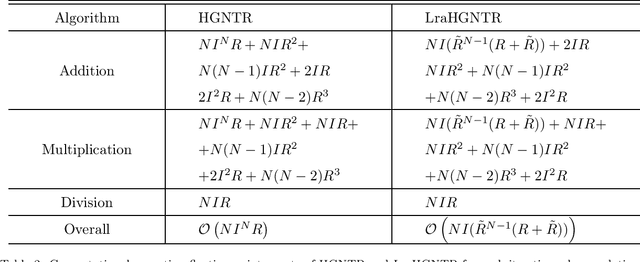
For the high dimensional data representation, nonnegative tensor ring (NTR) decomposition equipped with manifold learning has become a promising model to exploit the multi-dimensional structure and extract the feature from tensor data. However, the existing methods such as graph regularized tensor ring decomposition (GNTR) only models the pair-wise similarities of objects. For tensor data with complex manifold structure, the graph can not exactly construct similarity relationships. In this paper, in order to effectively utilize the higher-dimensional and complicated similarities among objects, we introduce hypergraph to the framework of NTR to further enhance the feature extraction, upon which a hypergraph regularized nonnegative tensor ring decomposition (HGNTR) method is developed. To reduce the computational complexity and suppress the noise, we apply the low-rank approximation trick to accelerate HGNTR (called LraHGNTR). Our experimental results show that compared with other state-of-the-art algorithms, the proposed HGNTR and LraHGNTR can achieve higher performance in clustering tasks, in addition, LraHGNTR can greatly reduce running time without decreasing accuracy.

Partially Shared Semi-supervised Deep Matrix Factorization with Multi-view Data

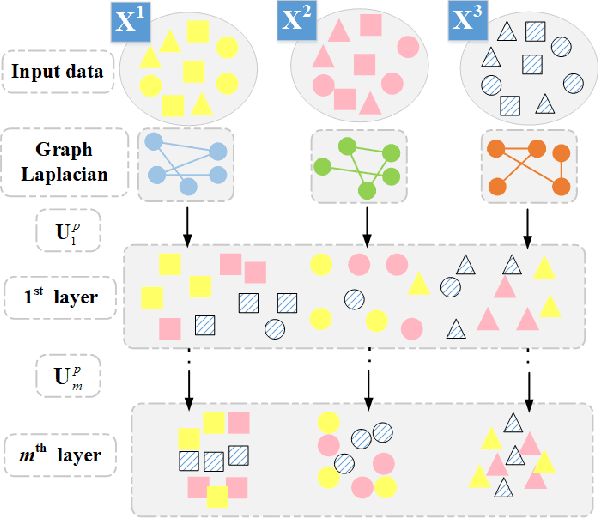
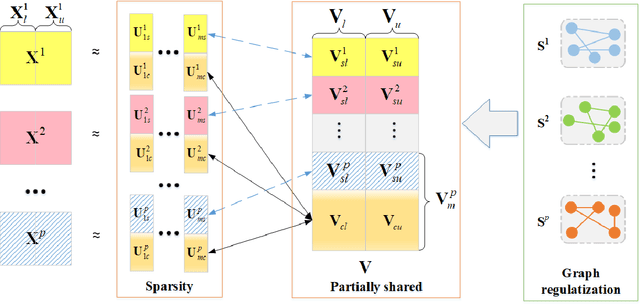
Since many real-world data can be described from multiple views, multi-view learning has attracted considerable attention. Various methods have been proposed and successfully applied to multi-view learning, typically based on matrix factorization models. Recently, it is extended to the deep structure to exploit the hierarchical information of multi-view data, but the view-specific features and the label information are seldom considered. To address these concerns, we present a partially shared semi-supervised deep matrix factorization model (PSDMF). By integrating the partially shared deep decomposition structure, graph regularization and the semi-supervised regression model, PSDMF can learn a compact and discriminative representation through eliminating the effects of uncorrelated information. In addition, we develop an efficient iterative updating algorithm for PSDMF. Extensive experiments on five benchmark datasets demonstrate that PSDMF can achieve better performance than the state-of-the-art multi-view learning approaches. The MATLAB source code is available at https://github.com/libertyhhn/PartiallySharedDMF.

An Efficient Tensor Completion Method via New Latent Nuclear Norm

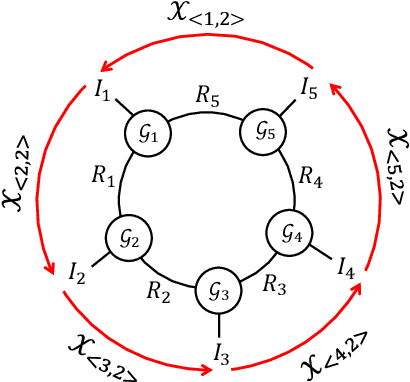
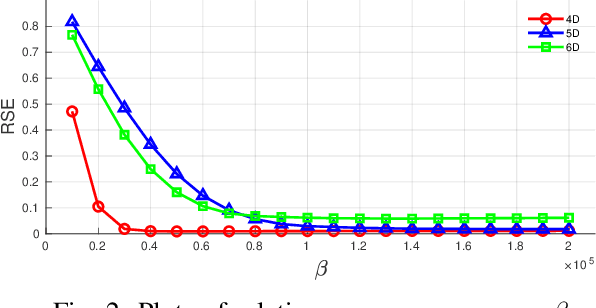
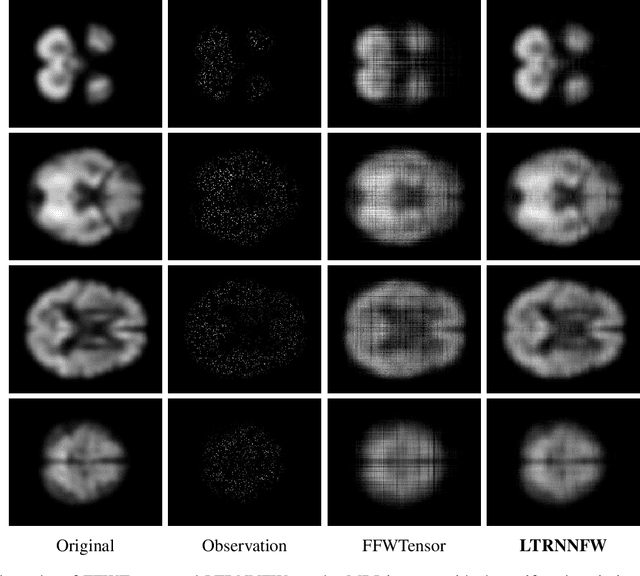
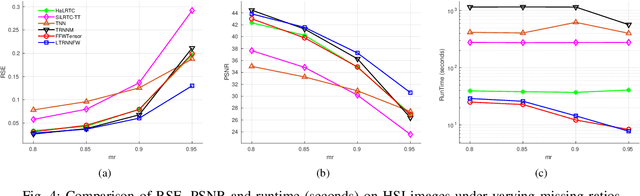
In tensor completion, the latent nuclear norm is commonly used to induce low-rank structure, while substantially failing to capture the global information due to the utilization of unbalanced unfolding scheme. To overcome this drawback, a new latent nuclear norm equipped with a more balanced unfolding scheme is defined for low-rank regularizer. Moreover, the new latent nuclear norm together with the Frank-Wolfe (FW) algorithm is developed as an efficient completion method by utilizing the sparsity structure of observed tensor. Specifically, both FW linear subproblem and line search only need to access the observed entries, by which we can instead maintain the sparse tensors and a set of small basis matrices during iteration. Most operations are based on sparse tensors, and the closed-form solution of FW linear subproblem can be obtained from rank-one SVD. We theoretically analyze the space-complexity and time-complexity of the proposed method, and show that it is much more efficient over other norm-based completion methods for higher-order tensors. Extensive experimental results of visual-data inpainting demonstrate that the proposed method is able to achieve state-of-the-art performance at smaller costs of time and space, which is very meaningful for the memory-limited equipment in practical applications.