Multi-view Data Classification with a Label-driven Auto-weighted Strategy

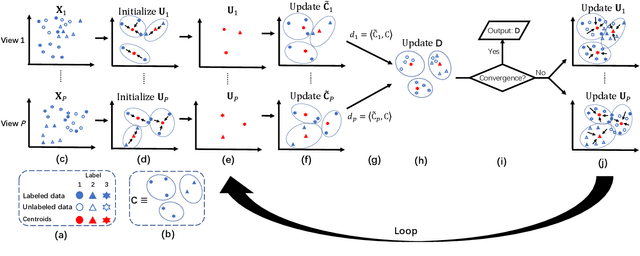
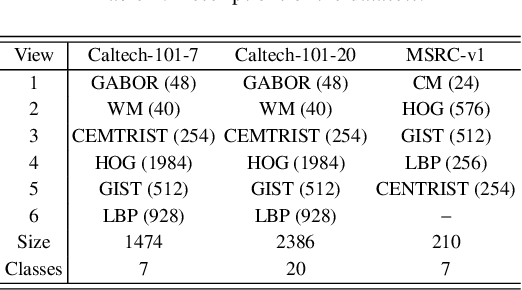
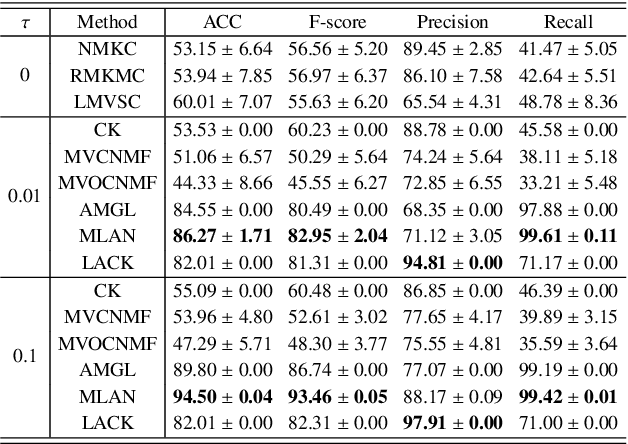
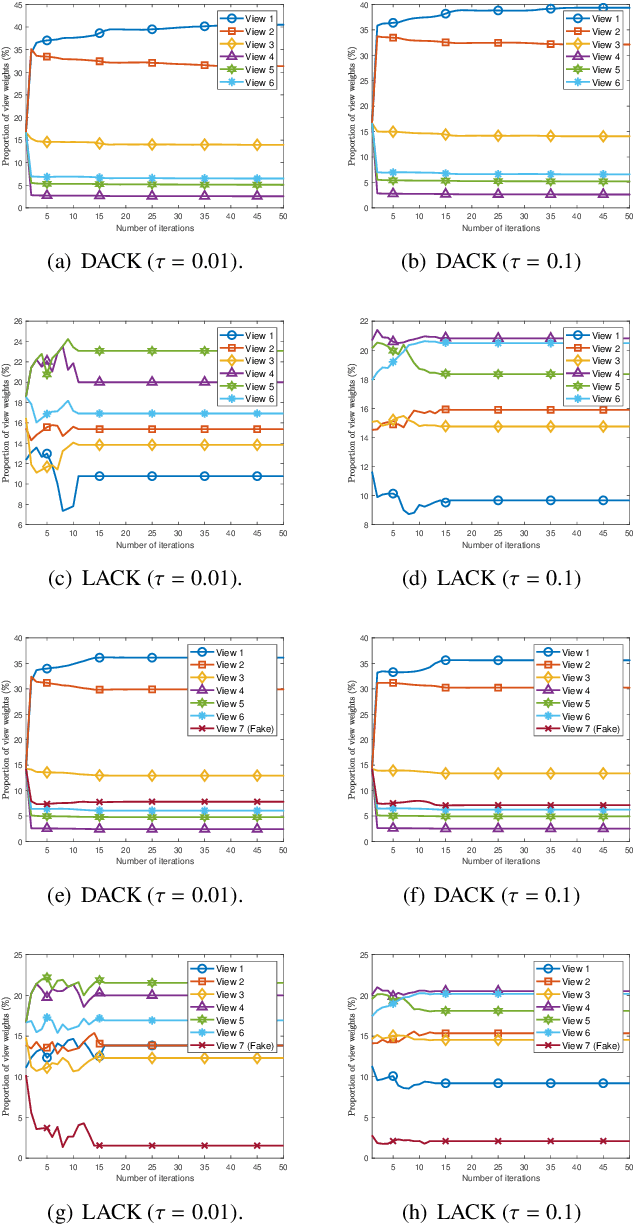
Distinguishing the importance of views has proven to be quite helpful for semi-supervised multi-view learning models. However, existing strategies cannot take advantage of semi-supervised information, only distinguishing the importance of views from a data feature perspective, which is often influenced by low-quality views then leading to poor performance. In this paper, by establishing a link between labeled data and the importance of different views, we propose an auto-weighted strategy to evaluate the importance of views from a label perspective to avoid the negative impact of unimportant or low-quality views. Based on this strategy, we propose a transductive semi-supervised auto-weighted multi-view classification model. The initialization of the proposed model can be effectively determined by labeled data, which is practical. The model is decoupled into three small-scale sub-problems that can efficiently be optimized with a local convergence guarantee. The experimental results on classification tasks show that the proposed method achieves optimal or sub-optimal classification accuracy at the lowest computational cost compared to other related methods, and the weight change experiments show that our proposed strategy can distinguish view importance more accurately than other related strategies on multi-view datasets with low-quality views.

Fast Hypergraph Regularized Nonnegative Tensor Ring Factorization Based on Low-Rank Approximation

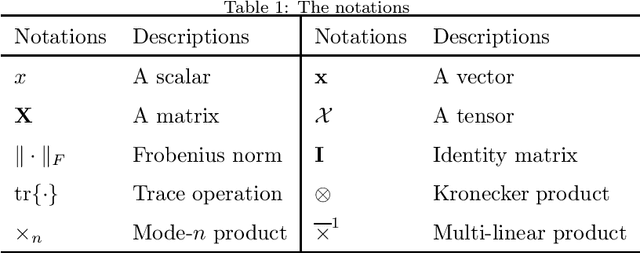
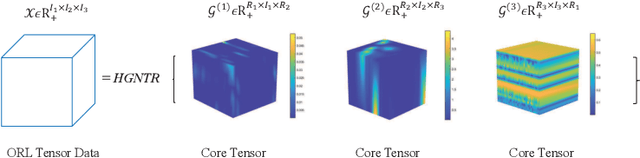
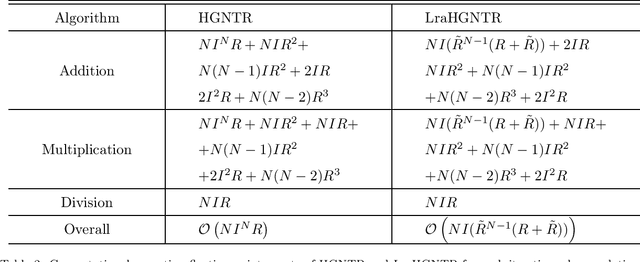
For the high dimensional data representation, nonnegative tensor ring (NTR) decomposition equipped with manifold learning has become a promising model to exploit the multi-dimensional structure and extract the feature from tensor data. However, the existing methods such as graph regularized tensor ring decomposition (GNTR) only models the pair-wise similarities of objects. For tensor data with complex manifold structure, the graph can not exactly construct similarity relationships. In this paper, in order to effectively utilize the higher-dimensional and complicated similarities among objects, we introduce hypergraph to the framework of NTR to further enhance the feature extraction, upon which a hypergraph regularized nonnegative tensor ring decomposition (HGNTR) method is developed. To reduce the computational complexity and suppress the noise, we apply the low-rank approximation trick to accelerate HGNTR (called LraHGNTR). Our experimental results show that compared with other state-of-the-art algorithms, the proposed HGNTR and LraHGNTR can achieve higher performance in clustering tasks, in addition, LraHGNTR can greatly reduce running time without decreasing accuracy.

Graph Regularized Nonnegative Tensor Ring Decomposition for Multiway Representation Learning

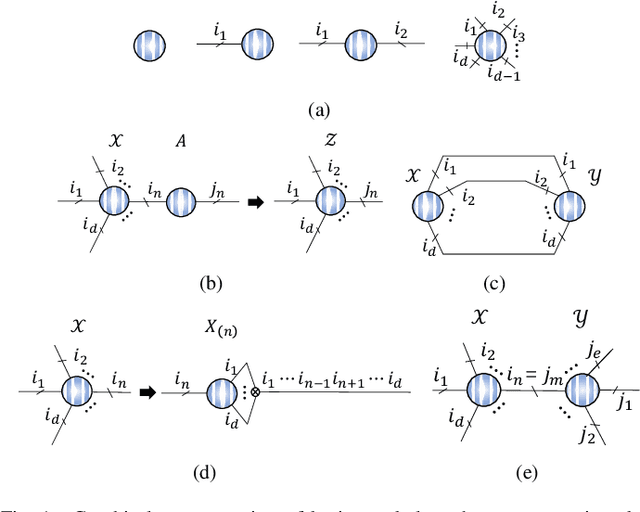
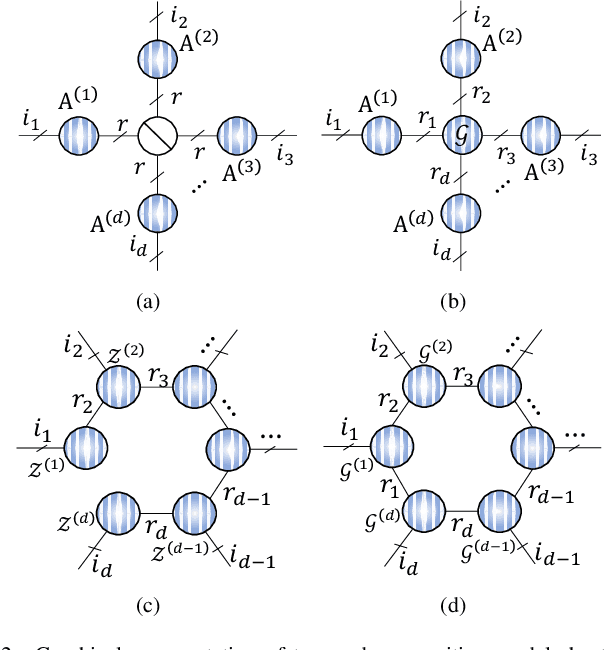
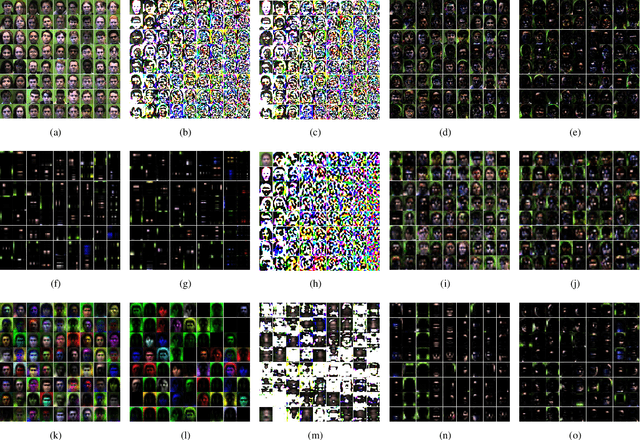
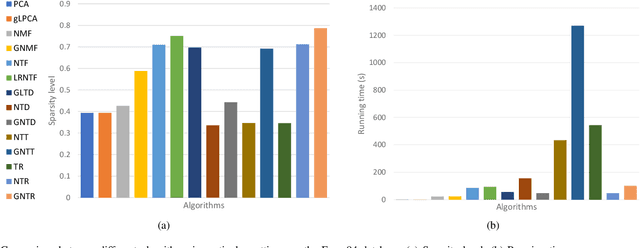
Tensor ring (TR) decomposition is a powerful tool for exploiting the low-rank nature of multiway data and has demonstrated great potential in a variety of important applications. In this paper, nonnegative tensor ring (NTR) decomposition and graph regularized NTR (GNTR) decomposition are proposed, where the former equips TR decomposition with local feature extraction by imposing nonnegativity on the core tensors and the latter is additionally able to capture manifold geometry information of tensor data, both significantly extend the applications of TR decomposition for nonnegative multiway representation learning. Accelerated proximal gradient based methods are derived for NTR and GNTR. The experimental result demonstrate that the proposed algorithms can extract parts-based basis with rich colors and rich lines from tensor objects that provide more interpretable and meaningful representation, and hence yield better performance than the state-of-the-art tensor based methods in clustering and classification tasks.