Graph Regularized Nonnegative Tensor Ring Decomposition for Multiway Representation Learning
Paper and Code
Oct 12, 2020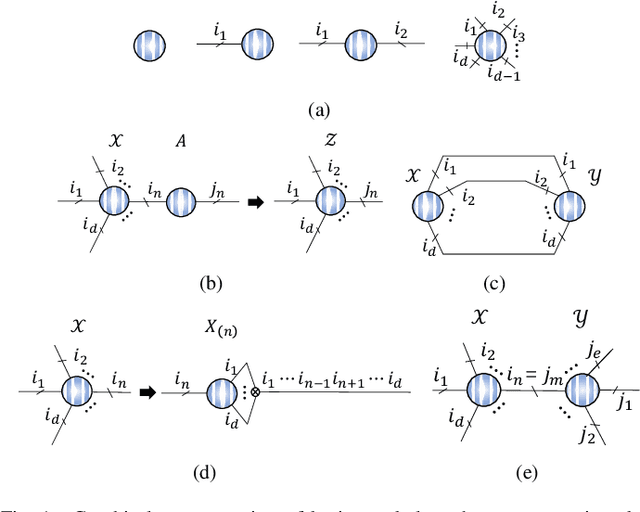
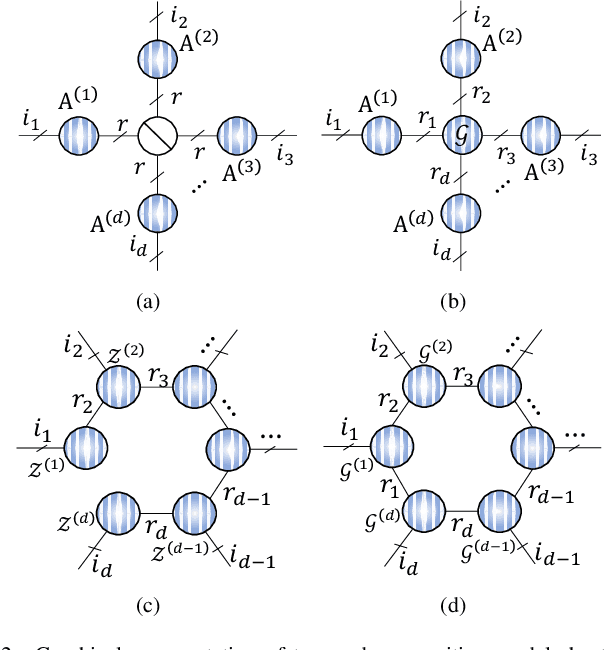
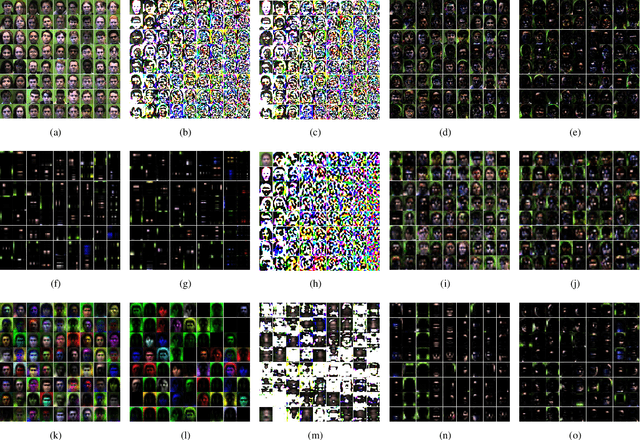
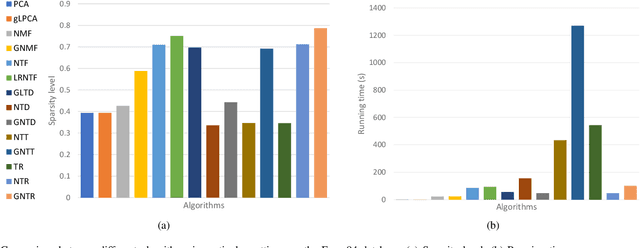
Tensor ring (TR) decomposition is a powerful tool for exploiting the low-rank nature of multiway data and has demonstrated great potential in a variety of important applications. In this paper, nonnegative tensor ring (NTR) decomposition and graph regularized NTR (GNTR) decomposition are proposed, where the former equips TR decomposition with local feature extraction by imposing nonnegativity on the core tensors and the latter is additionally able to capture manifold geometry information of tensor data, both significantly extend the applications of TR decomposition for nonnegative multiway representation learning. Accelerated proximal gradient based methods are derived for NTR and GNTR. The experimental result demonstrate that the proposed algorithms can extract parts-based basis with rich colors and rich lines from tensor objects that provide more interpretable and meaningful representation, and hence yield better performance than the state-of-the-art tensor based methods in clustering and classification tasks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge