Qinbin Zhao
Latent Matrices for Tensor Network Decomposition and to Tensor Completion
Oct 07, 2022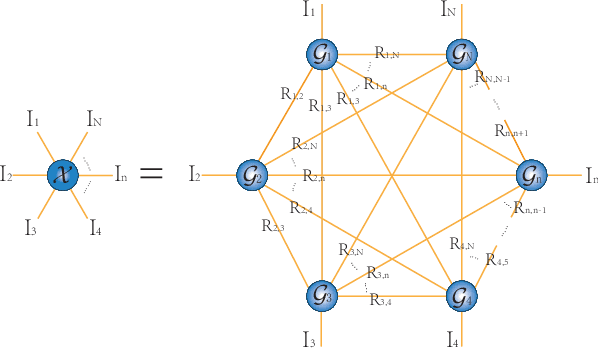
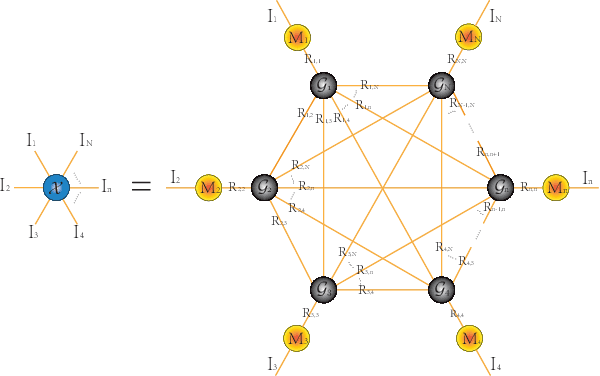
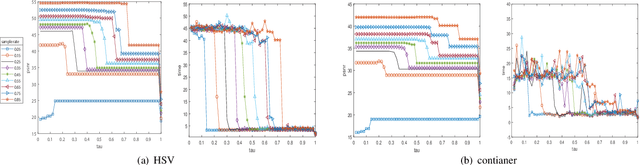
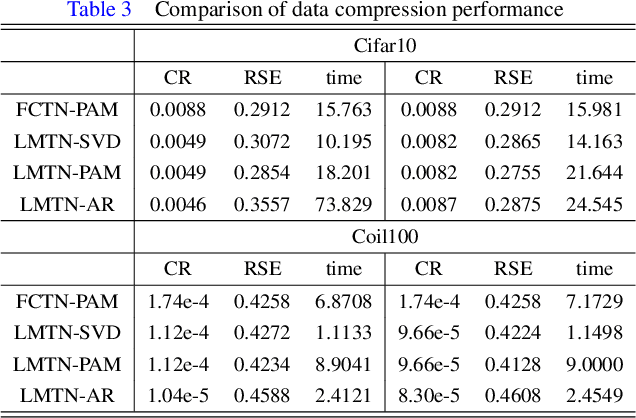
Abstract:The prevalent fully-connected tensor network (FCTN) has achieved excellent success to compress data. However, the FCTN decomposition suffers from slow computational speed when facing higher-order and large-scale data. Naturally, there arises an interesting question: can a new model be proposed that decomposes the tensor into smaller ones and speeds up the computation of the algorithm? This work gives a positive answer by formulating a novel higher-order tensor decomposition model that utilizes latent matrices based on the tensor network structure, which can decompose a tensor into smaller-scale data than the FCTN decomposition, hence we named it Latent Matrices for Tensor Network Decomposition (LMTN). Furthermore, three optimization algorithms, LMTN-PAM, LMTN-SVD and LMTN-AR, have been developed and applied to the tensor-completion task. In addition, we provide proofs of theoretical convergence and complexity analysis for these algorithms. Experimental results show that our algorithm has the effectiveness in both deep learning dataset compression and higher-order tensor completion, and that our LMTN-SVD algorithm is 3-6 times faster than the FCTN-PAM algorithm and only a 1.8 points accuracy drop.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge