Understanding Convolutional Neural Networks from Theoretical Perspective via Volterra Convolution

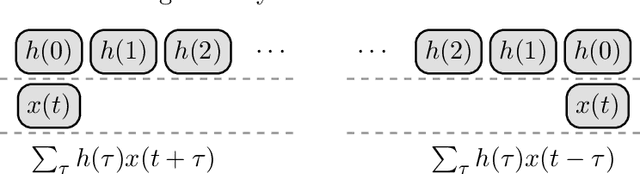
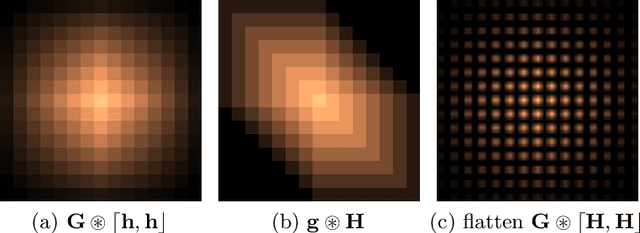
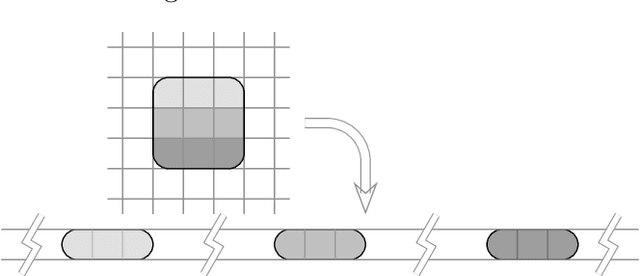
This study proposes a general and unified perspective of convolutional neural networks by exploring the relationship between (deep) convolutional neural networks and finite Volterra convolutions. It provides a novel approach to explain and study the overall characteristics of neural networks without being disturbed by the complex network architectures. Concretely, we examine the basic structures of finite term Volterra convolutions and convolutional neural networks. Our results show that convolutional neural network is an approximation of the finite term Volterra convolution, whose order increases exponentially with the number of layers and kernel size increases exponentially with the strides. With this perspective, the specialized perturbations are directly obtained from the approximated kernels rather than iterative generated adversarial examples. Extensive experiments on synthetic and real-world data sets show the correctness and effectiveness of our results.