Discovering More Effective Tensor Network Structure Search Algorithms via Large Language Models (LLMs)

Tensor network structure search (TN-SS), aiming at searching for suitable tensor network (TN) structures in representing high-dimensional problems, largely promotes the efficacy of TN in various machine learning applications. Nonetheless, finding a satisfactory TN structure using existing algorithms remains challenging. To develop more effective algorithms and avoid the human labor-intensive development process, we explore the knowledge embedded in large language models (LLMs) for the automatic design of TN-SS algorithms. Our approach, dubbed GPTN-SS, leverages an elaborate crafting LLM-based prompting system that operates in an evolutionary-like manner. The experimental results, derived from real-world data, demonstrate that GPTN-SS can effectively leverage the insights gained from existing methods to develop novel TN-SS algorithms that achieve a better balance between exploration and exploitation. These algorithms exhibit superior performance in searching the high-quality TN structures for natural image compression and model parameters compression while also demonstrating generalizability in their performance.

SVDinsTN: An Integrated Method for Tensor Network Representation with Efficient Structure Search

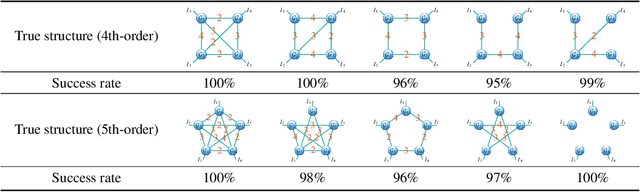
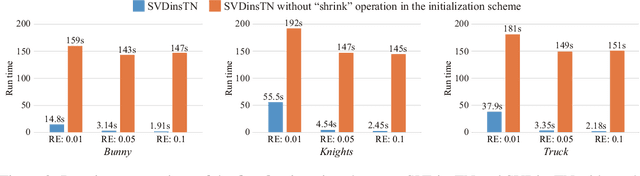
Tensor network (TN) representation is a powerful technique for data analysis and machine learning. It practically involves a challenging TN structure search (TN-SS) problem, which aims to search for the optimal structure to achieve a compact representation. Existing TN-SS methods mainly adopt a bi-level optimization method that leads to excessive computational costs due to repeated structure evaluations. To address this issue, we propose an efficient integrated (single-level) method named SVD-inspired TN decomposition (SVDinsTN), eliminating the need for repeated tedious structure evaluation. By inserting a diagonal factor for each edge of the fully-connected TN, we calculate TN cores and diagonal factors simultaneously, with factor sparsity revealing the most compact TN structure. Experimental results on real-world data demonstrate that SVDinsTN achieves approximately $10^2\sim{}10^3$ times acceleration in runtime compared to the existing TN-SS methods while maintaining a comparable level of representation ability.

Alternating Local Enumeration (TnALE): Solving Tensor Network Structure Search with Fewer Evaluations

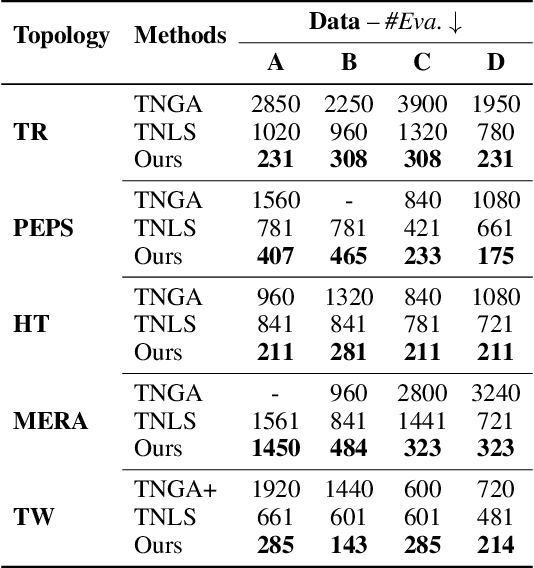
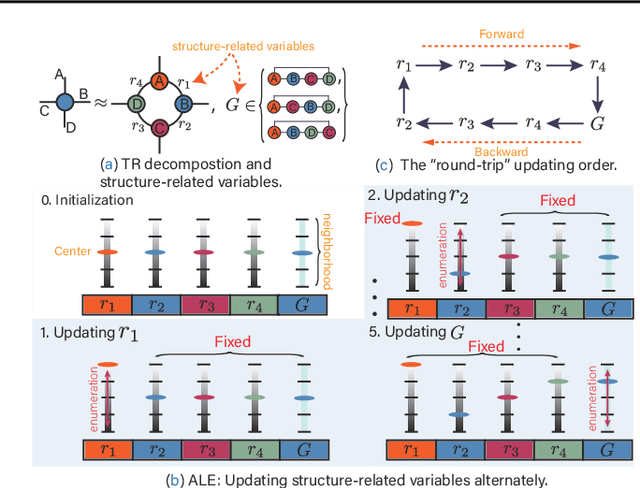
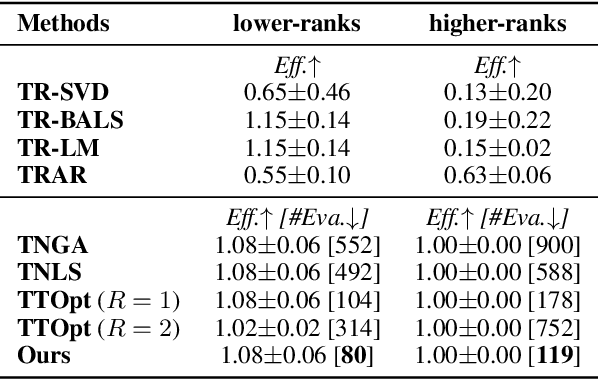
Tensor network (TN) is a powerful framework in machine learning, but selecting a good TN model, known as TN structure search (TN-SS), is a challenging and computationally intensive task. The recent approach TNLS~\cite{li2022permutation} showed promising results for this task, however, its computational efficiency is still unaffordable, requiring too many evaluations of the objective function. We propose TnALE, a new algorithm that updates each structure-related variable alternately by local enumeration, \emph{greatly} reducing the number of evaluations compared to TNLS. We theoretically investigate the descent steps for TNLS and TnALE, proving that both algorithms can achieve linear convergence up to a constant if a sufficient reduction of the objective is \emph{reached} in each neighborhood. We also compare the evaluation efficiency of TNLS and TnALE, revealing that $\Omega(2^N)$ evaluations are typically required in TNLS for \emph{reaching} the objective reduction in the neighborhood, while ideally $O(N^2R)$ evaluations are sufficient in TnALE, where $N$ denotes the tensor order and $R$ reflects the \emph{``low-rankness''} of the neighborhood. Experimental results verify that TnALE can find practically good TN-ranks and permutations with vastly fewer evaluations than the state-of-the-art algorithms.

Permutation Search of Tensor Network Structures via Local Sampling

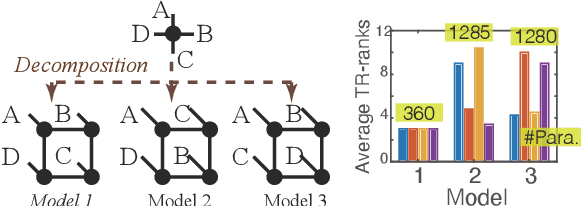
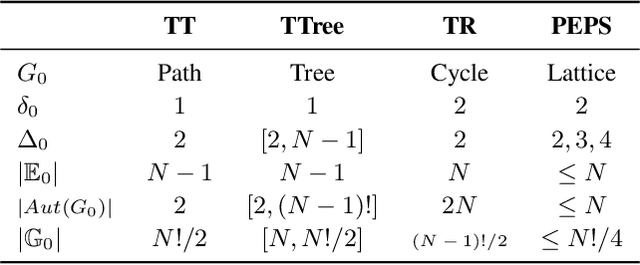
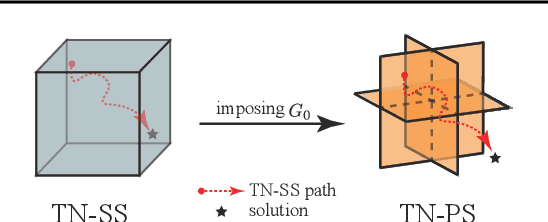
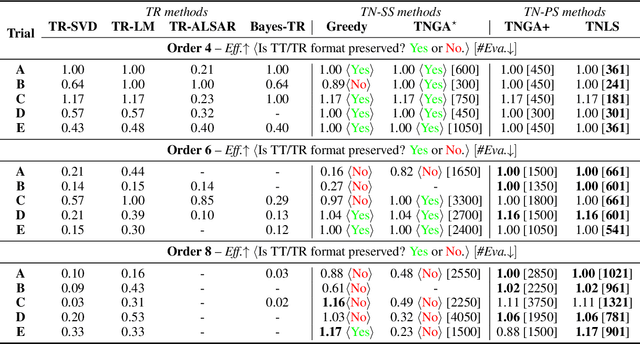
Recent works put much effort into tensor network structure search (TN-SS), aiming to select suitable tensor network (TN) structures, involving the TN-ranks, formats, and so on, for the decomposition or learning tasks. In this paper, we consider a practical variant of TN-SS, dubbed TN permutation search (TN-PS), in which we search for good mappings from tensor modes onto TN vertices (core tensors) for compact TN representations. We conduct a theoretical investigation of TN-PS and propose a practically-efficient algorithm to resolve the problem. Theoretically, we prove the counting and metric properties of search spaces of TN-PS, analyzing for the first time the impact of TN structures on these unique properties. Numerically, we propose a novel meta-heuristic algorithm, in which the searching is done by randomly sampling in a neighborhood established in our theory, and then recurrently updating the neighborhood until convergence. Numerical results demonstrate that the new algorithm can reduce the required model size of TNs in extensive benchmarks, implying the improvement in the expressive power of TNs. Furthermore, the computational cost for the new algorithm is significantly less than that in~\cite{li2020evolutionary}.