Xi-Le Zhao
Gaussian Splatting-based Low-Rank Tensor Representation for Multi-Dimensional Image Recovery
Nov 19, 2025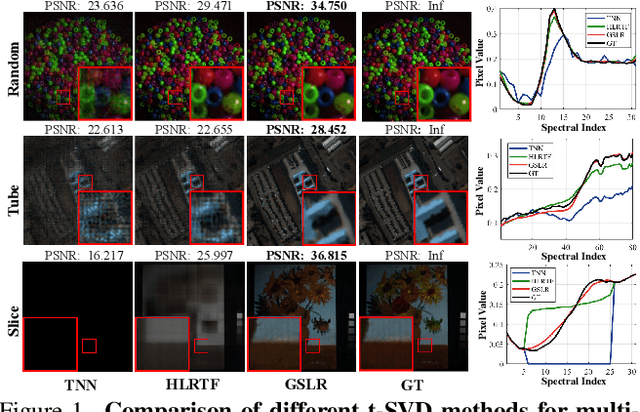
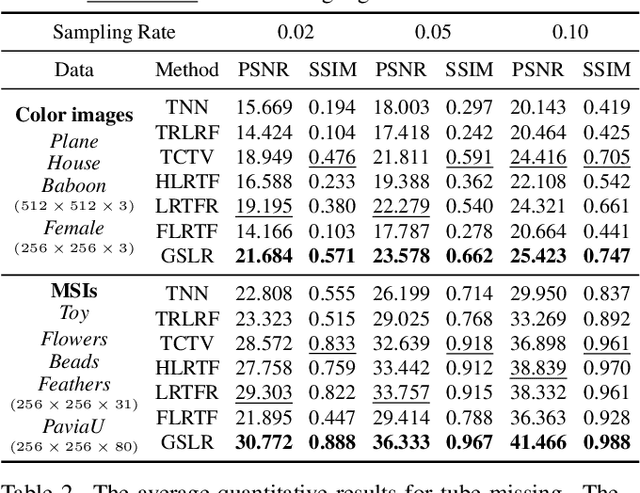
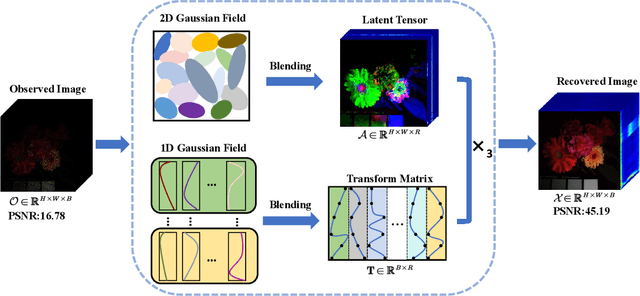
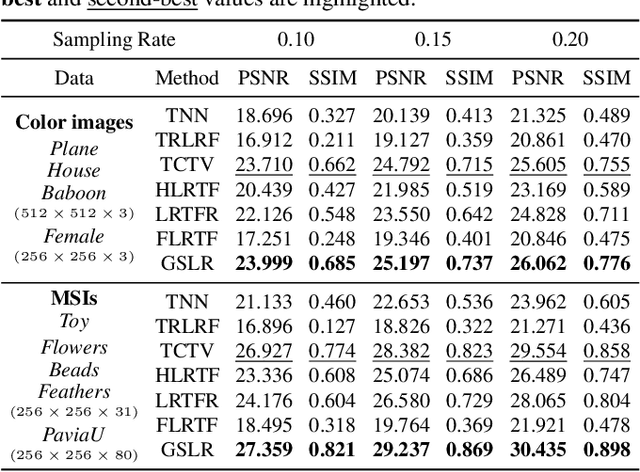
Abstract:Tensor singular value decomposition (t-SVD) is a promising tool for multi-dimensional image representation, which decomposes a multi-dimensional image into a latent tensor and an accompanying transform matrix. However, two critical limitations of t-SVD methods persist: (1) the approximation of the latent tensor (e.g., tensor factorizations) is coarse and fails to accurately capture spatial local high-frequency information; (2) The transform matrix is composed of fixed basis atoms (e.g., complex exponential atoms in DFT and cosine atoms in DCT) and cannot precisely capture local high-frequency information along the mode-3 fibers. To address these two limitations, we propose a Gaussian Splatting-based Low-rank tensor Representation (GSLR) framework, which compactly and continuously represents multi-dimensional images. Specifically, we leverage tailored 2D Gaussian splatting and 1D Gaussian splatting to generate the latent tensor and transform matrix, respectively. The 2D and 1D Gaussian splatting are indispensable and complementary under this representation framework, which enjoys a powerful representation capability, especially for local high-frequency information. To evaluate the representation ability of the proposed GSLR, we develop an unsupervised GSLR-based multi-dimensional image recovery model. Extensive experiments on multi-dimensional image recovery demonstrate that GSLR consistently outperforms state-of-the-art methods, particularly in capturing local high-frequency information.
Hyperspectral Anomaly Detection Fused Unified Nonconvex Tensor Ring Factors Regularization
May 23, 2025Abstract:In recent years, tensor decomposition-based approaches for hyperspectral anomaly detection (HAD) have gained significant attention in the field of remote sensing. However, existing methods often fail to fully leverage both the global correlations and local smoothness of the background components in hyperspectral images (HSIs), which exist in both the spectral and spatial domains. This limitation results in suboptimal detection performance. To mitigate this critical issue, we put forward a novel HAD method named HAD-EUNTRFR, which incorporates an enhanced unified nonconvex tensor ring (TR) factors regularization. In the HAD-EUNTRFR framework, the raw HSIs are first decomposed into background and anomaly components. The TR decomposition is then employed to capture the spatial-spectral correlations within the background component. Additionally, we introduce a unified and efficient nonconvex regularizer, induced by tensor singular value decomposition (TSVD), to simultaneously encode the low-rankness and sparsity of the 3-D gradient TR factors into a unique concise form. The above characterization scheme enables the interpretable gradient TR factors to inherit the low-rankness and smoothness of the original background. To further enhance anomaly detection, we design a generalized nonconvex regularization term to exploit the group sparsity of the anomaly component. To solve the resulting doubly nonconvex model, we develop a highly efficient optimization algorithm based on the alternating direction method of multipliers (ADMM) framework. Experimental results on several benchmark datasets demonstrate that our proposed method outperforms existing state-of-the-art (SOTA) approaches in terms of detection accuracy.
DTR: A Unified Deep Tensor Representation Framework for Multimedia Data Recovery
Jul 07, 2024



Abstract:Recently, the transform-based tensor representation has attracted increasing attention in multimedia data (e.g., images and videos) recovery problems, which consists of two indispensable components, i.e., transform and characterization. Previously, the development of transform-based tensor representation mainly focuses on the transform aspect. Although several attempts consider using shallow matrix factorization (e.g., singular value decomposition and negative matrix factorization) to characterize the frontal slices of transformed tensor (termed as latent tensor), the faithful characterization aspect is underexplored. To address this issue, we propose a unified Deep Tensor Representation (termed as DTR) framework by synergistically combining the deep latent generative module and the deep transform module. Especially, the deep latent generative module can faithfully generate the latent tensor as compared with shallow matrix factorization. The new DTR framework not only allows us to better understand the classic shallow representations, but also leads us to explore new representation. To examine the representation ability of the proposed DTR, we consider the representative multi-dimensional data recovery task and suggest an unsupervised DTR-based multi-dimensional data recovery model. Extensive experiments demonstrate that DTR achieves superior performance compared to state-of-the-art methods in both quantitative and qualitative aspects, especially for fine details recovery.
Low-Tubal-Rank Tensor Recovery via Factorized Gradient Descent
Feb 03, 2024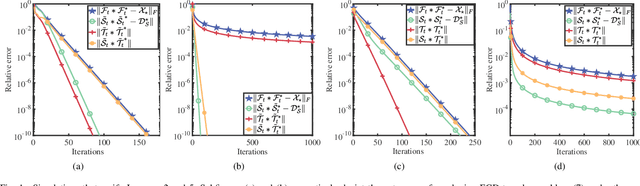
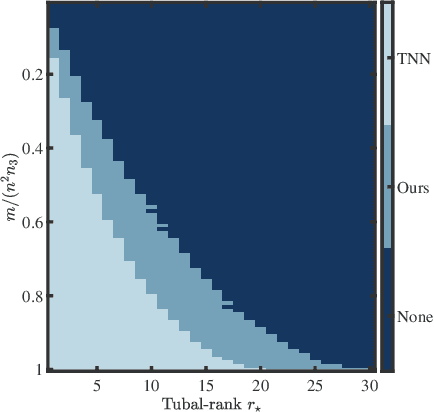
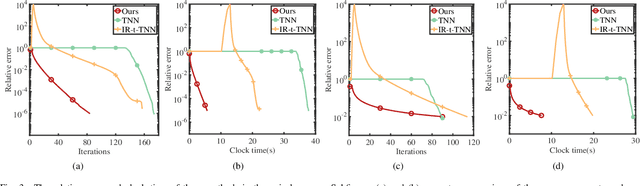
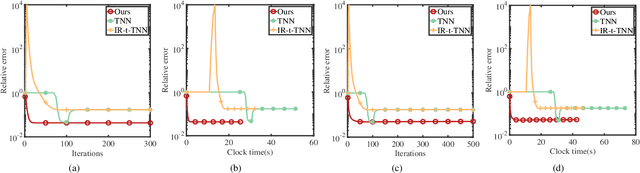
Abstract:This paper considers the problem of recovering a tensor with an underlying low-tubal-rank structure from a small number of corrupted linear measurements. Traditional approaches tackling such a problem require the computation of tensor Singular Value Decomposition (t-SVD), that is a computationally intensive process, rendering them impractical for dealing with large-scale tensors. Aim to address this challenge, we propose an efficient and effective low-tubal-rank tensor recovery method based on a factorization procedure akin to the Burer-Monteiro (BM) method. Precisely, our fundamental approach involves decomposing a large tensor into two smaller factor tensors, followed by solving the problem through factorized gradient descent (FGD). This strategy eliminates the need for t-SVD computation, thereby reducing computational costs and storage requirements. We provide rigorous theoretical analysis to ensure the convergence of FGD under both noise-free and noisy situations. Additionally, it is worth noting that our method does not require the precise estimation of the tensor tubal-rank. Even in cases where the tubal-rank is slightly overestimated, our approach continues to demonstrate robust performance. A series of experiments have been carried out to demonstrate that, as compared to other popular ones, our approach exhibits superior performance in multiple scenarios, in terms of the faster computational speed and the smaller convergence error.
SVDinsTN: An Integrated Method for Tensor Network Representation with Efficient Structure Search
May 24, 2023

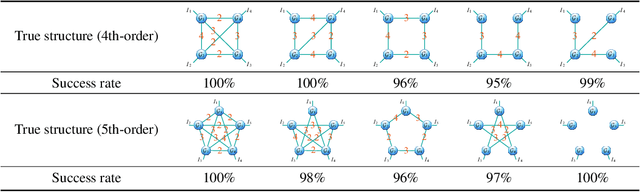
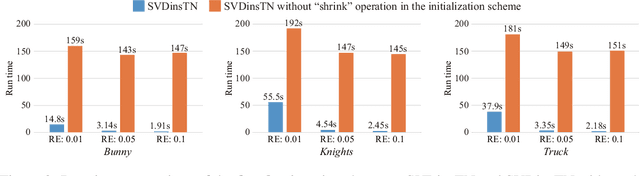
Abstract:Tensor network (TN) representation is a powerful technique for data analysis and machine learning. It practically involves a challenging TN structure search (TN-SS) problem, which aims to search for the optimal structure to achieve a compact representation. Existing TN-SS methods mainly adopt a bi-level optimization method that leads to excessive computational costs due to repeated structure evaluations. To address this issue, we propose an efficient integrated (single-level) method named SVD-inspired TN decomposition (SVDinsTN), eliminating the need for repeated tedious structure evaluation. By inserting a diagonal factor for each edge of the fully-connected TN, we calculate TN cores and diagonal factors simultaneously, with factor sparsity revealing the most compact TN structure. Experimental results on real-world data demonstrate that SVDinsTN achieves approximately $10^2\sim{}10^3$ times acceleration in runtime compared to the existing TN-SS methods while maintaining a comparable level of representation ability.
Fast and Structured Block-Term Tensor Decomposition For Hyperspectral Unmixing
May 08, 2022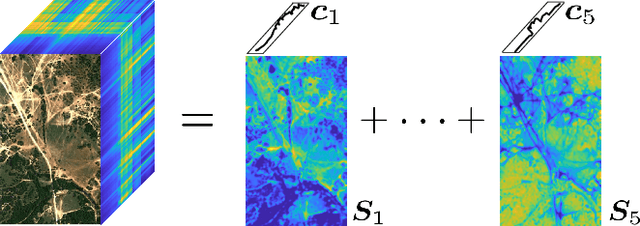
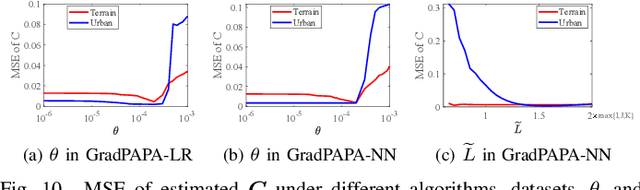
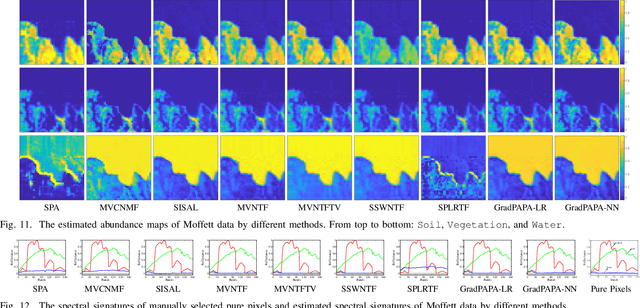
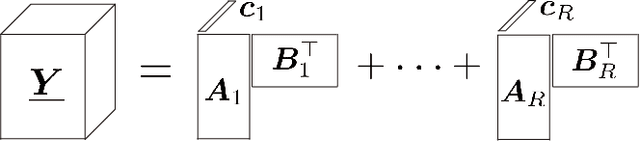
Abstract:The block-term tensor decomposition model with multilinear rank-$(L_r,L_r,1)$ terms (or, the "LL1 tensor decomposition" in short) offers a valuable alternative for hyperspectral unmixing (HU) under the linear mixture model. Particularly, the LL1 decomposition ensures the endmember/abundance identifiability in scenarios where such guarantees are not supported by the classic matrix factorization (MF) approaches. However, existing LL1-based HU algorithms use a three-factor parameterization of the tensor (i.e., the hyperspectral image cube), which leads to a number of challenges including high per-iteration complexity, slow convergence, and difficulties in incorporating structural prior information. This work puts forth an LL1 tensor decomposition-based HU algorithm that uses a constrained two-factor re-parameterization of the tensor data. As a consequence, a two-block alternating gradient projection (GP)-based LL1 algorithm is proposed for HU. With carefully designed projection solvers, the GP algorithm enjoys a relatively low per-iteration complexity. Like in MF-based HU, the factors under our parameterization correspond to the endmembers and abundances. Thus, the proposed framework is natural to incorporate physics-motivated priors that arise in HU. The proposed algorithm often attains orders-of-magnitude speedup and substantial HU performance gains compared to the existing three-factor parameterization-based HU algorithms.
Nonstationary Temporal Matrix Factorization for Multivariate Time Series Forecasting
Mar 20, 2022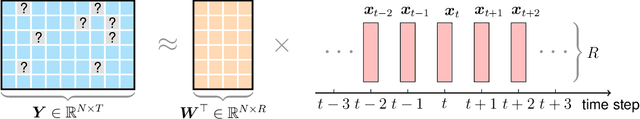
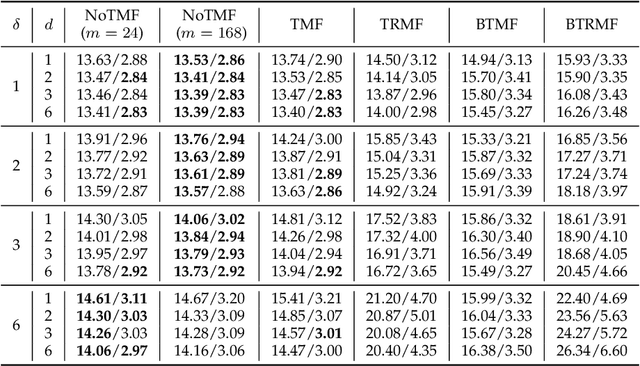
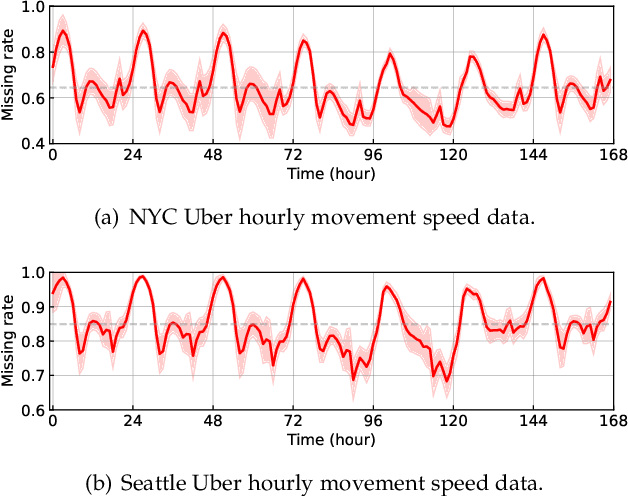
Abstract:Modern time series datasets are often high-dimensional, incomplete/sparse, and nonstationary. These properties hinder the development of scalable and efficient solutions for time series forecasting and analysis. To address these challenges, we propose a Nonstationary Temporal Matrix Factorization (NoTMF) model, in which matrix factorization is used to reconstruct the whole time series matrix and vector autoregressive (VAR) process is imposed on a properly differenced copy of the temporal factor matrix. This approach not only preserves the low-rank property of the data but also offers consistent temporal dynamics. The learning process of NoTMF involves the optimization of two factor matrices and a collection of VAR coefficient matrices. To efficiently solve the optimization problem, we derive an alternating minimization framework, in which subproblems are solved using conjugate gradient and least squares methods. In particular, the use of conjugate gradient method offers an efficient routine and allows us to apply NoTMF on large-scale problems. Through extensive experiments on Uber movement speed dataset, we demonstrate the superior accuracy and effectiveness of NoTMF over other baseline models. Our results also confirm the importance of addressing the nonstationarity of real-world time series data such as spatiotemporal traffic flow/speed.
Nonlinear Transform Induced Tensor Nuclear Norm for Tensor Completion
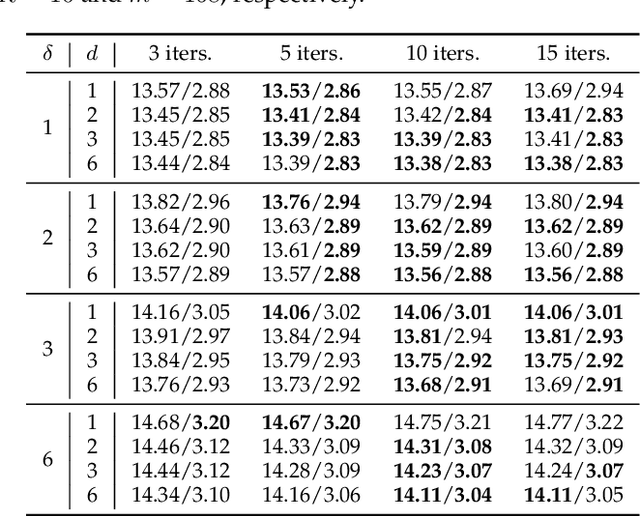
Oct 17, 2021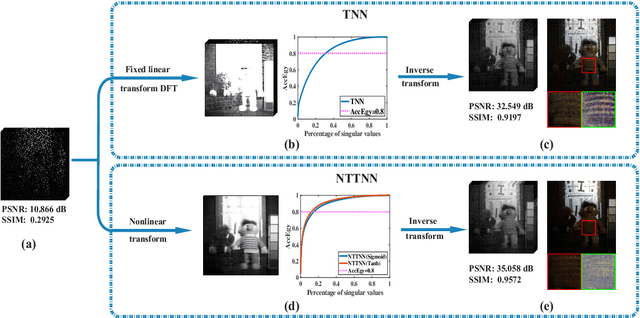

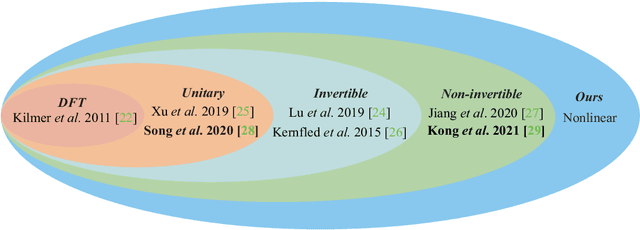
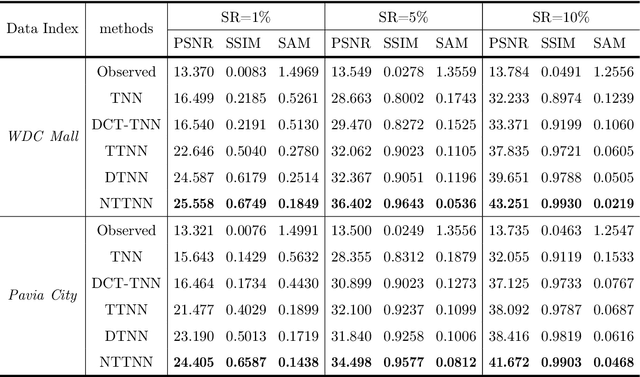
Abstract:The linear transform-based tensor nuclear norm (TNN) methods have recently obtained promising results for tensor completion. The main idea of this type of methods is exploiting the low-rank structure of frontal slices of the targeted tensor under the linear transform along the third mode. However, the low-rankness of frontal slices is not significant under linear transforms family. To better pursue the low-rank approximation, we propose a nonlinear transform-based TNN (NTTNN). More concretely, the proposed nonlinear transform is a composite transform consisting of the linear semi-orthogonal transform along the third mode and the element-wise nonlinear transform on frontal slices of the tensor under the linear semi-orthogonal transform, which are indispensable and complementary in the composite transform to fully exploit the underlying low-rankness. Based on the suggested low-rankness metric, i.e., NTTNN, we propose a low-rank tensor completion (LRTC) model. To tackle the resulting nonlinear and nonconvex optimization model, we elaborately design the proximal alternating minimization (PAM) algorithm and establish the theoretical convergence guarantee of the PAM algorithm. Extensive experimental results on hyperspectral images, multispectral images, and videos show that the our method outperforms linear transform-based state-of-the-art LRTC methods qualitatively and quantitatively.
Fully-Connected Tensor Network Decomposition for Robust Tensor Completion Problem
Oct 17, 2021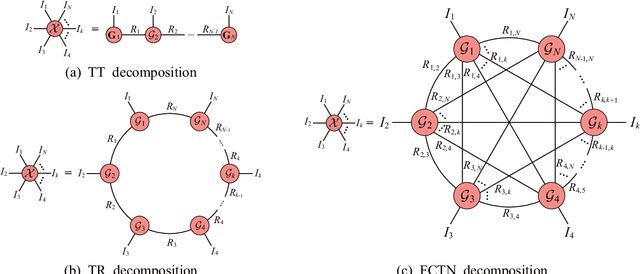
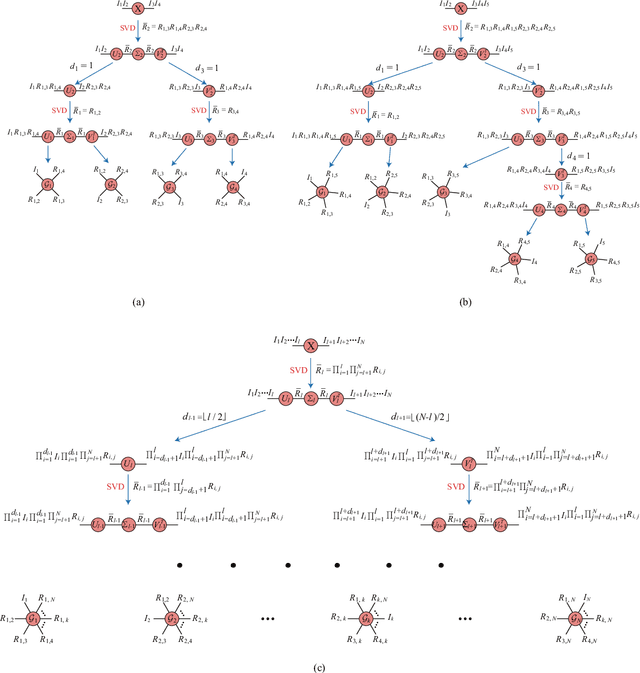
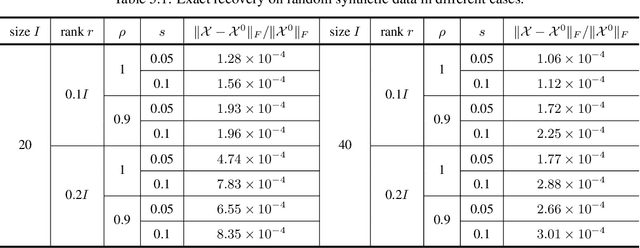
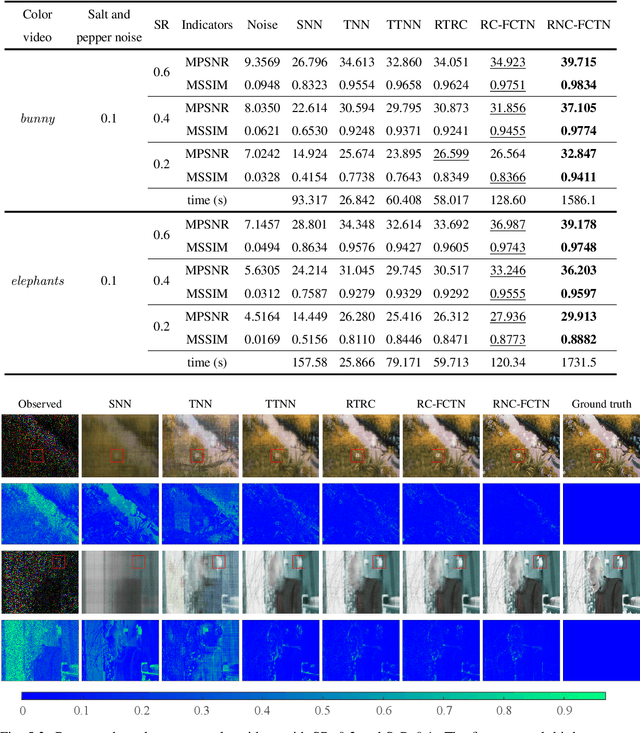
Abstract:The robust tensor completion (RTC) problem, which aims to reconstruct a low-rank tensor from partially observed tensor contaminated by a sparse tensor, has received increasing attention. In this paper, by leveraging the superior expression of the fully-connected tensor network (FCTN) decomposition, we propose a $\textbf{FCTN}$-based $\textbf{r}$obust $\textbf{c}$onvex optimization model (RC-FCTN) for the RTC problem. Then, we rigorously establish the exact recovery guarantee for the RC-FCTN. For solving the constrained optimization model RC-FCTN, we develop an alternating direction method of multipliers (ADMM)-based algorithm, which enjoys the global convergence guarantee. Moreover, we suggest a $\textbf{FCTN}$-based $\textbf{r}$obust $\textbf{n}$on$\textbf{c}$onvex optimization model (RNC-FCTN) for the RTC problem. A proximal alternating minimization (PAM)-based algorithm is developed to solve the proposed RNC-FCTN. Meanwhile, we theoretically derive the convergence of the PAM-based algorithm. Comprehensive numerical experiments in several applications, such as video completion and video background subtraction, demonstrate that proposed methods are superior to several state-of-the-art methods.
Nonlocal Patch-Based Fully-Connected Tensor Network Decomposition for Remote Sensing Image Inpainting
Sep 13, 2021
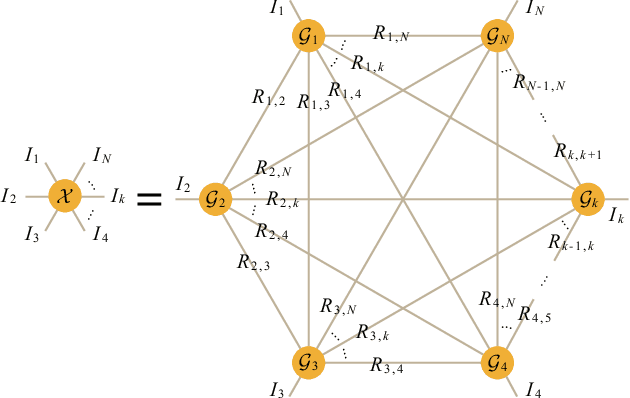


Abstract:Remote sensing image (RSI) inpainting plays an important role in real applications. Recently, fully-connected tensor network (FCTN) decomposition has been shown the remarkable ability to fully characterize the global correlation. Considering the global correlation and the nonlocal self-similarity (NSS) of RSIs, this paper introduces the FCTN decomposition to the whole RSI and its NSS groups, and proposes a novel nonlocal patch-based FCTN (NL-FCTN) decomposition for RSI inpainting. Different from other nonlocal patch-based methods, the NL-FCTN decomposition-based method, which increases tensor order by stacking similar small-sized patches to NSS groups, cleverly leverages the remarkable ability of FCTN decomposition to deal with higher-order tensors. Besides, we propose an efficient proximal alternating minimization-based algorithm to solve the proposed NL-FCTN decomposition-based model with a theoretical convergence guarantee. Extensive experiments on RSIs demonstrate that the proposed method achieves the state-of-the-art inpainting performance in all compared methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge