Implicit Neural Feature Fusion Function for Multispectral and Hyperspectral Image Fusion

Multispectral and Hyperspectral Image Fusion (MHIF) is a practical task that aims to fuse a high-resolution multispectral image (HR-MSI) and a low-resolution hyperspectral image (LR-HSI) of the same scene to obtain a high-resolution hyperspectral image (HR-HSI). Benefiting from powerful inductive bias capability, CNN-based methods have achieved great success in the MHIF task. However, they lack certain interpretability and require convolution structures be stacked to enhance performance. Recently, Implicit Neural Representation (INR) has achieved good performance and interpretability in 2D tasks due to its ability to locally interpolate samples and utilize multimodal content such as pixels and coordinates. Although INR-based approaches show promise, they require extra construction of high-frequency information (\emph{e.g.,} positional encoding). In this paper, inspired by previous work of MHIF task, we realize that HR-MSI could serve as a high-frequency detail auxiliary input, leading us to propose a novel INR-based hyperspectral fusion function named Implicit Neural Feature Fusion Function (INF). As an elaborate structure, it solves the MHIF task and addresses deficiencies in the INR-based approaches. Specifically, our INF designs a Dual High-Frequency Fusion (DHFF) structure that obtains high-frequency information twice from HR-MSI and LR-HSI, then subtly fuses them with coordinate information. Moreover, the proposed INF incorporates a parameter-free method named INR with cosine similarity (INR-CS) that uses cosine similarity to generate local weights through feature vectors. Based on INF, we construct an Implicit Neural Fusion Network (INFN) that achieves state-of-the-art performance for MHIF tasks of two public datasets, \emph{i.e.,} CAVE and Harvard. The code will soon be made available on GitHub.

LAConv: Local Adaptive Convolution for Image Fusion

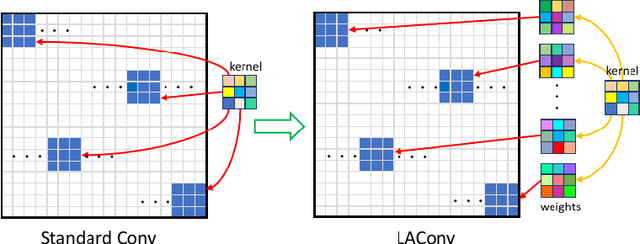
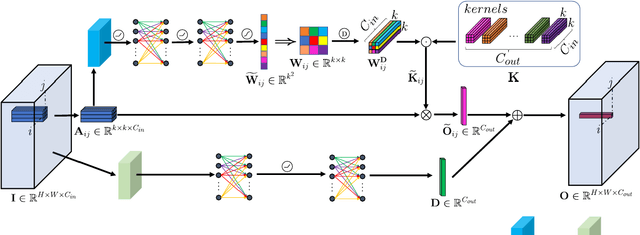
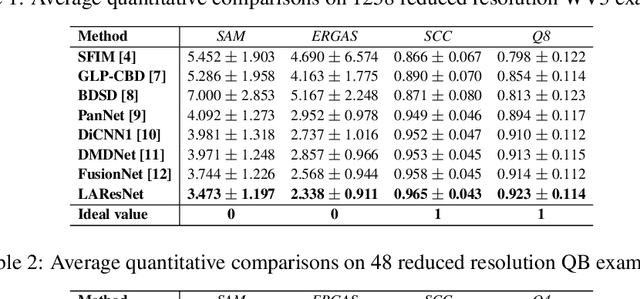
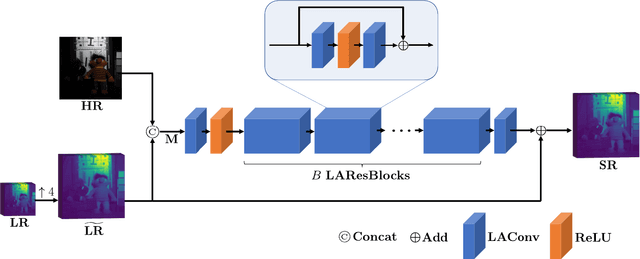
The convolution operation is a powerful tool for feature extraction and plays a prominent role in the field of computer vision. However, when targeting the pixel-wise tasks like image fusion, it would not fully perceive the particularity of each pixel in the image if the uniform convolution kernel is used on different patches. In this paper, we propose a local adaptive convolution (LAConv), which is dynamically adjusted to different spatial locations. LAConv enables the network to pay attention to every specific local area in the learning process. Besides, the dynamic bias (DYB) is introduced to provide more possibilities for the depiction of features and make the network more flexible. We further design a residual structure network equipped with the proposed LAConv and DYB modules, and apply it to two image fusion tasks. Experiments for pansharpening and hyperspectral image super-resolution (HISR) demonstrate the superiority of our method over other state-of-the-art methods. It is worth mentioning that LAConv can also be competent for other super-resolution tasks with less computation effort.

Self-Supervised Nonlinear Transform-Based Tensor Nuclear Norm for Multi-Dimensional Image Recovery

In this paper, we study multi-dimensional image recovery. Recently, transform-based tensor nuclear norm minimization methods are considered to capture low-rank tensor structures to recover third-order tensors in multi-dimensional image processing applications. The main characteristic of such methods is to perform the linear transform along the third mode of third-order tensors, and then compute tensor nuclear norm minimization on the transformed tensor so that the underlying low-rank tensors can be recovered. The main aim of this paper is to propose a nonlinear multilayer neural network to learn a nonlinear transform via the observed tensor data under self-supervision. The proposed network makes use of low-rank representation of transformed tensors and data-fitting between the observed tensor and the reconstructed tensor to construct the nonlinear transformation. Extensive experimental results on tensor completion, background subtraction, robust tensor completion, and snapshot compressive imaging are presented to demonstrate that the performance of the proposed method is better than that of state-of-the-art methods.

Dictionary Learning with Low-rank Coding Coefficients for Tensor Completion

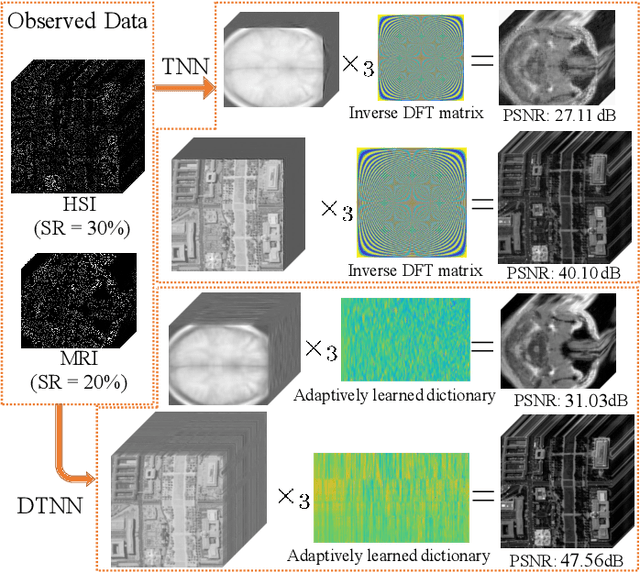
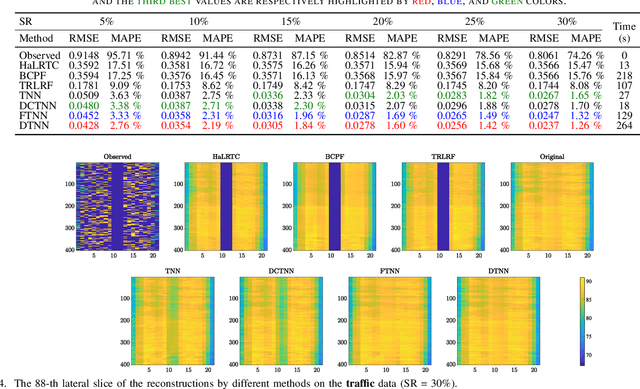
In this paper, we propose a novel tensor learning and coding model for third-order data completion. Our model is to learn a data-adaptive dictionary from the given observations, and determine the coding coefficients of third-order tensor tubes. In the completion process, we minimize the low-rankness of each tensor slice containing the coding coefficients. By comparison with the traditional pre-defined transform basis, the advantages of the proposed model are that (i) the dictionary can be learned based on the given data observations so that the basis can be more adaptively and accurately constructed, and (ii) the low-rankness of the coding coefficients can allow the linear combination of dictionary features more effectively. Also we develop a multi-block proximal alternating minimization algorithm for solving such tensor learning and coding model, and show that the sequence generated by the algorithm can globally converge to a critical point. Extensive experimental results for real data sets such as videos, hyperspectral images, and traffic data are reported to demonstrate these advantages and show the performance of the proposed tensor learning and coding method is significantly better than the other tensor completion methods in terms of several evaluation metrics.

Tangent Space Based Alternating Projections for Nonnegative Low Rank Matrix Approximation

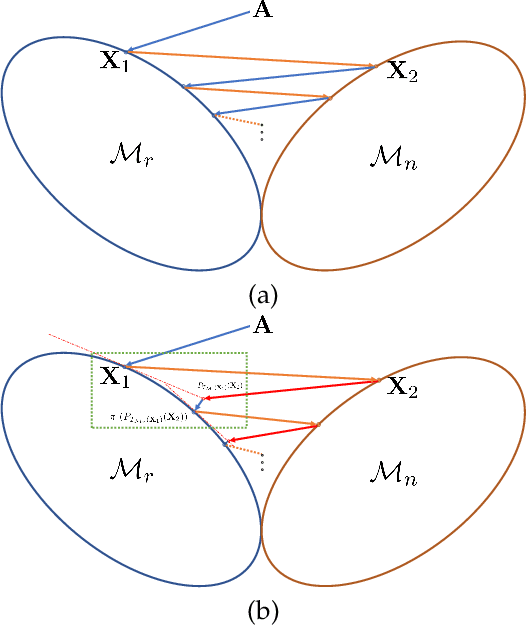
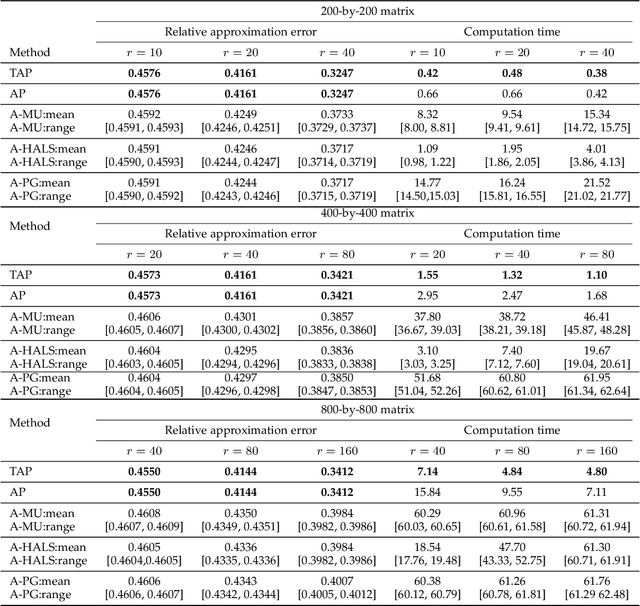
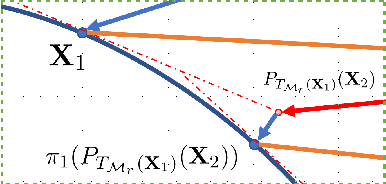
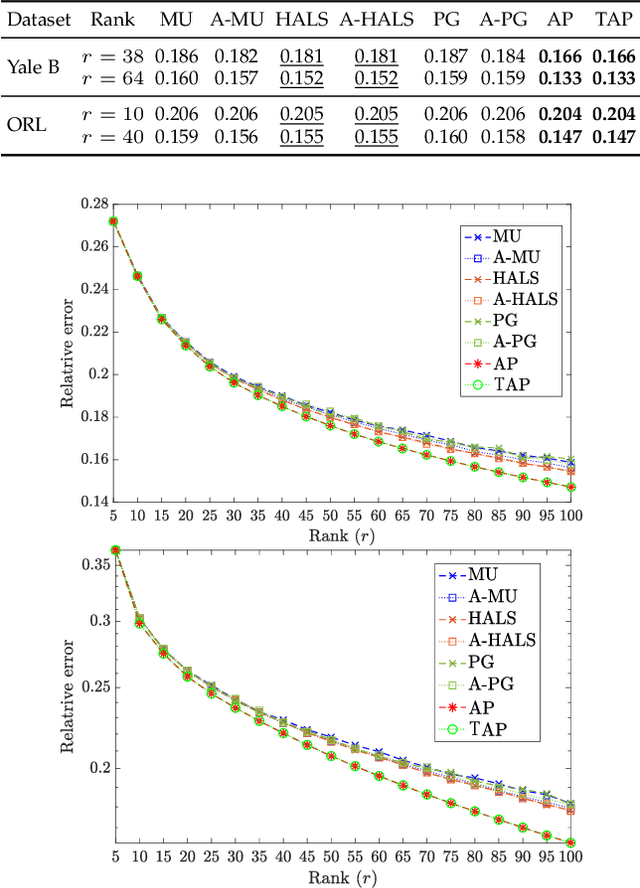
In this paper, we develop a new alternating projection method to compute nonnegative low rank matrix approximation for nonnegative matrices. In the nonnegative low rank matrix approximation method, the projection onto the manifold of fixed rank matrices can be expensive as the singular value decomposition is required. We propose to use the tangent space of the point in the manifold to approximate the projection onto the manifold in order to reduce the computational cost. We show that the sequence generated by the alternating projections onto the tangent spaces of the fixed rank matrices manifold and the nonnegative matrix manifold, converge linearly to a point in the intersection of the two manifolds where the convergent point is sufficiently close to optimal solutions. This convergence result based inexact projection onto the manifold is new and is not studied in the literature. Numerical examples in data clustering, pattern recognition and hyperspectral data analysis are given to demonstrate that the performance of the proposed method is better than that of nonnegative matrix factorization methods in terms of computational time and accuracy.

Unsupervised Hyperspectral Mixed Noise Removal Via Spatial-Spectral Constrained Deep Image Prior

Hyperspectral images (HSIs) are unavoidably corrupted by mixed noise which hinders the subsequent applications. Traditional methods exploit the structure of the HSI via optimization-based models for denoising, while their capacity is inferior to the convolutional neural network (CNN)-based methods, which supervisedly learn the noisy-to-denoised mapping from a large amount of data. However, as the clean-noisy pairs of hyperspectral data are always unavailable in many applications, it is eager to build an unsupervised HSI denoising method with high model capability. To remove the mixed noise in HSIs, we suggest the spatial-spectral constrained deep image prior (S2DIP), which simultaneously capitalize the high model representation ability brought by the CNN in an unsupervised manner and does not need any extra training data. Specifically, we employ the separable 3D convolution blocks to faithfully encode the HSI in the framework of DIP, and a spatial-spectral total variation (SSTV) term is tailored to explore the spatial-spectral smoothness of HSIs. Moreover, our method favorably addresses the semi-convergence behavior of prevailing unsupervised methods, e.g., DIP 2D, and DIP 3D. Extensive experiments demonstrate that the proposed method outperforms state-of-the-art optimization-based HSI denoising methods in terms of effectiveness and robustness.

Nonnegative Low Rank Tensor Approximation and its Application to Multi-dimensional Images

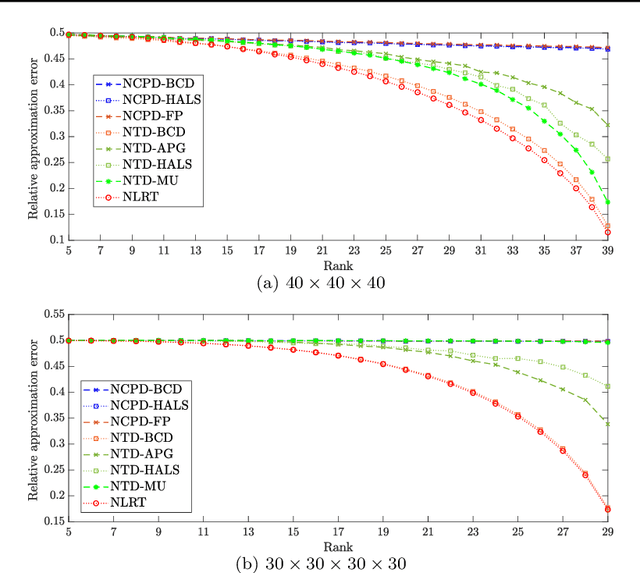
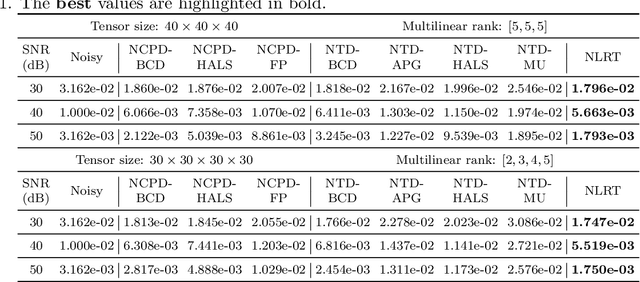
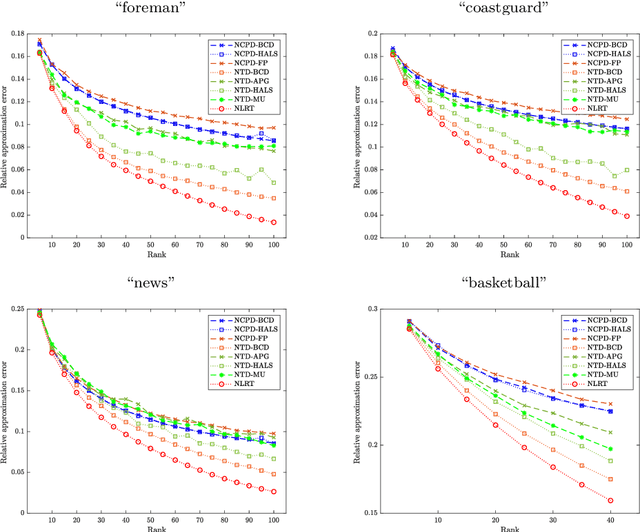
The main aim of this paper is to develop a new algorithm for computing Nonnegative Low Rank Tensor (NLRT) approximation for nonnegative tensors that arise in many multi-dimensional imaging applications. Nonnegativity is one of the important property as each pixel value refer to nonzero light intensity in image data acquisition. Our approach is different from classical nonnegative tensor factorization (NTF) which has been studied for many years. For a given nonnegative tensor, the classical NTF approach is to determine nonnegative low rank tensor by computing factor matrices or tensors (for example, CPD finds factor matrices while Tucker decomposition finds core tensor and factor matrices), such that the distance between this nonnegative low rank tensor and given tensor is as small as possible. The proposed NLRT approach is different from the classical NTF. It determines a nonnegative low rank tensor without using decompositions or factorization methods. The minimized distance by the proposed NLRT method can be smaller than that by the NTF method, and it implies that the proposed NLRT method can obtain a better low rank tensor approximation. The proposed NLRT approximation algorithm is derived by using the alternating averaged projection on the product of low rank matrix manifolds and non-negativity property. We show the convergence of the alternating projection algorithm. Experimental results for synthetic data and multi-dimensional images are presented to demonstrate the performance of the proposed NLRT method is better than that of existing NTF methods.

Hyperspectral Image Super-resolution via Deep Spatio-spectral Convolutional Neural Networks

Hyperspectral images are of crucial importance in order to better understand features of different materials. To reach this goal, they leverage on a high number of spectral bands. However, this interesting characteristic is often paid by a reduced spatial resolution compared with traditional multispectral image systems. In order to alleviate this issue, in this work, we propose a simple and efficient architecture for deep convolutional neural networks to fuse a low-resolution hyperspectral image (LR-HSI) and a high-resolution multispectral image (HR-MSI), yielding a high-resolution hyperspectral image (HR-HSI). The network is designed to preserve both spatial and spectral information thanks to an architecture from two folds: one is to utilize the HR-HSI at a different scale to get an output with a satisfied spectral preservation; another one is to apply concepts of multi-resolution analysis to extract high-frequency information, aiming to output high quality spatial details. Finally, a plain mean squared error loss function is used to measure the performance during the training. Extensive experiments demonstrate that the proposed network architecture achieves best performance (both qualitatively and quantitatively) compared with recent state-of-the-art hyperspectral image super-resolution approaches. Moreover, other significant advantages can be pointed out by the use of the proposed approach, such as, a better network generalization ability, a limited computational burden, and a robustness with respect to the number of training samples.

Framelet Representation of Tensor Nuclear Norm for Third-Order Tensor Completion

The main aim of this paper is to develop a framelet representation of the tensor nuclear norm for third-order tensor completion. In the literature, the tensor nuclear norm can be computed by using tensor singular value decomposition based on the discrete Fourier transform matrix, and tensor completion can be performed by the minimization of the tensor nuclear norm which is the relaxation of the sum of matrix ranks from all Fourier transformed matrix frontal slices. These Fourier transformed matrix frontal slices are obtained by applying the discrete Fourier transform on the tubes of the original tensor. In this paper, we propose to employ the framelet representation of each tube so that a framelet transformed tensor can be constructed. Because of framelet basis redundancy, the representation of each tube is sparsely represented. When the matrix slices of the original tensor are highly correlated, we expect the corresponding sum of matrix ranks from all framelet transformed matrix frontal slices would be small, and the resulting tensor completion can be performed much better. The proposed minimization model is convex and global minimizers can be obtained. Numerical results on several types of multi-dimensional data (videos, multispectral images, and magnetic resonance imaging data) have tested and shown that the proposed method outperformed the other testing tensor completion methods.

Constrained low-tubal-rank tensor recovery for hyperspectral images mixed noise removal by bilateral random projections

In this paper, we propose a novel low-tubal-rank tensor recovery model, which directly constrains the tubal rank prior for effectively removing the mixed Gaussian and sparse noise in hyperspectral images. The constraints of tubal-rank and sparsity can govern the solution of the denoised tensor in the recovery procedure. To solve the constrained low-tubal-rank model, we develop an iterative algorithm based on bilateral random projections to efficiently solve the proposed model. The advantage of random projections is that the approximation of the low-tubal-rank tensor can be obtained quite accurately in an inexpensive manner. Experimental examples for hyperspectral image denoising are presented to demonstrate the effectiveness and efficiency of the proposed method.