Tangent Space Based Alternating Projections for Nonnegative Low Rank Matrix Approximation

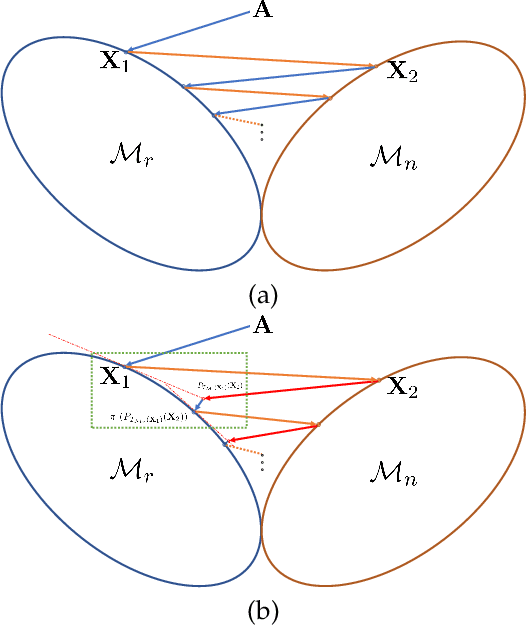
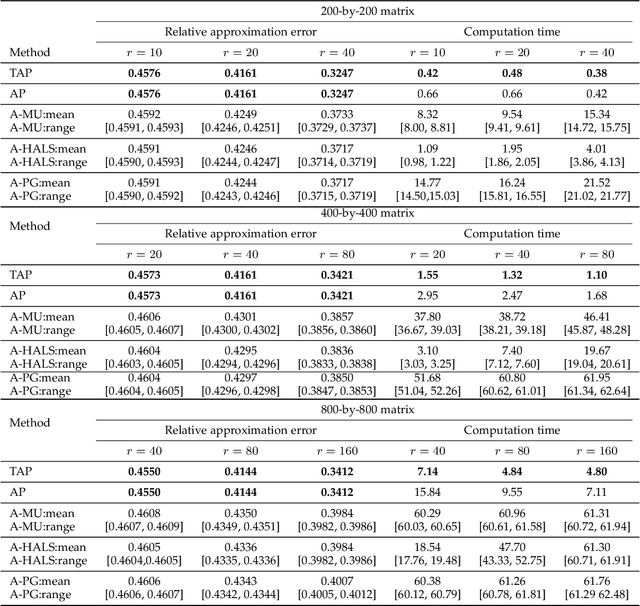
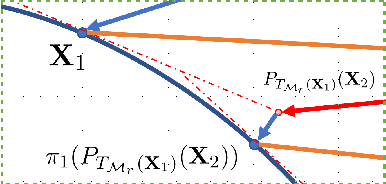
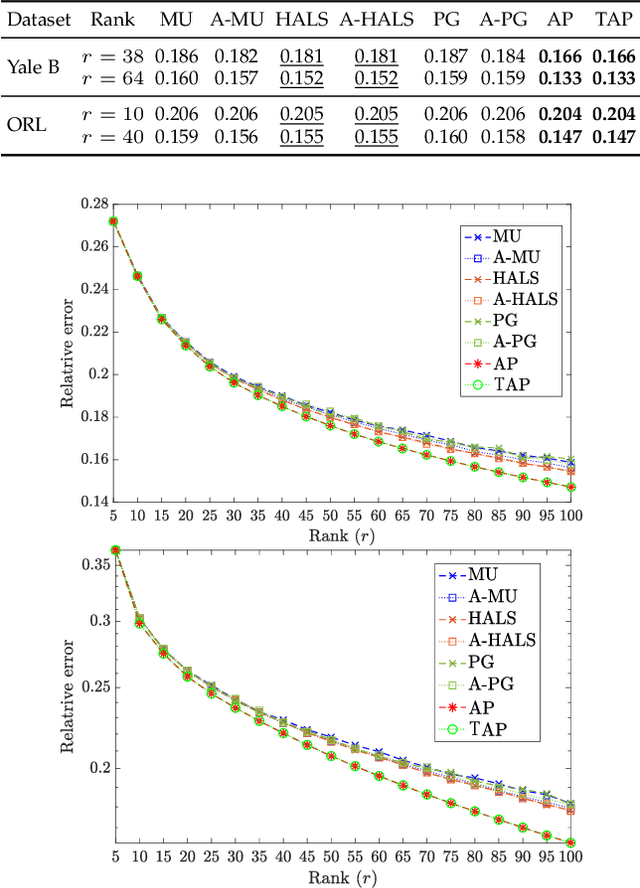
In this paper, we develop a new alternating projection method to compute nonnegative low rank matrix approximation for nonnegative matrices. In the nonnegative low rank matrix approximation method, the projection onto the manifold of fixed rank matrices can be expensive as the singular value decomposition is required. We propose to use the tangent space of the point in the manifold to approximate the projection onto the manifold in order to reduce the computational cost. We show that the sequence generated by the alternating projections onto the tangent spaces of the fixed rank matrices manifold and the nonnegative matrix manifold, converge linearly to a point in the intersection of the two manifolds where the convergent point is sufficiently close to optimal solutions. This convergence result based inexact projection onto the manifold is new and is not studied in the literature. Numerical examples in data clustering, pattern recognition and hyperspectral data analysis are given to demonstrate that the performance of the proposed method is better than that of nonnegative matrix factorization methods in terms of computational time and accuracy.

Nonnegative Low Rank Tensor Approximation and its Application to Multi-dimensional Images

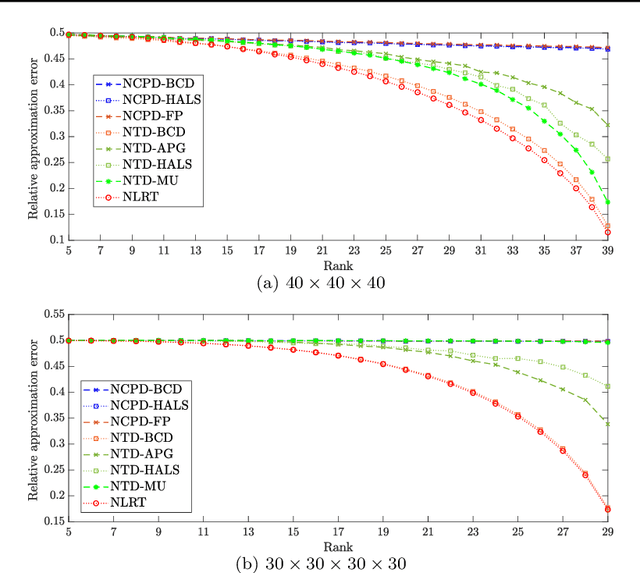
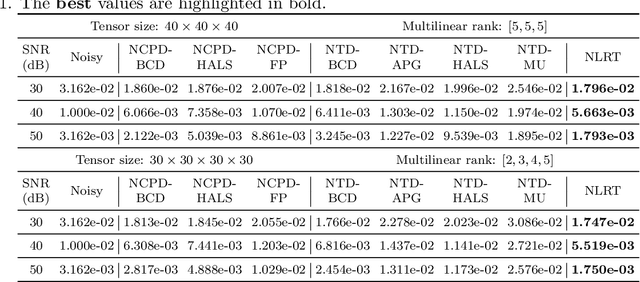
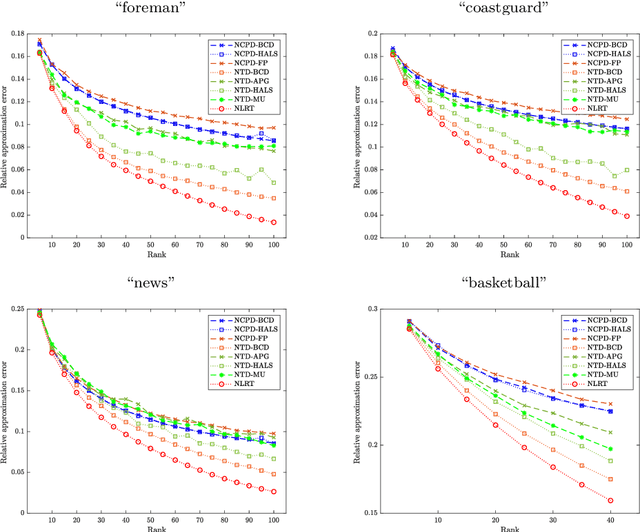
The main aim of this paper is to develop a new algorithm for computing Nonnegative Low Rank Tensor (NLRT) approximation for nonnegative tensors that arise in many multi-dimensional imaging applications. Nonnegativity is one of the important property as each pixel value refer to nonzero light intensity in image data acquisition. Our approach is different from classical nonnegative tensor factorization (NTF) which has been studied for many years. For a given nonnegative tensor, the classical NTF approach is to determine nonnegative low rank tensor by computing factor matrices or tensors (for example, CPD finds factor matrices while Tucker decomposition finds core tensor and factor matrices), such that the distance between this nonnegative low rank tensor and given tensor is as small as possible. The proposed NLRT approach is different from the classical NTF. It determines a nonnegative low rank tensor without using decompositions or factorization methods. The minimized distance by the proposed NLRT method can be smaller than that by the NTF method, and it implies that the proposed NLRT method can obtain a better low rank tensor approximation. The proposed NLRT approximation algorithm is derived by using the alternating averaged projection on the product of low rank matrix manifolds and non-negativity property. We show the convergence of the alternating projection algorithm. Experimental results for synthetic data and multi-dimensional images are presented to demonstrate the performance of the proposed NLRT method is better than that of existing NTF methods.

Robust Tensor Completion Using Transformed Tensor SVD

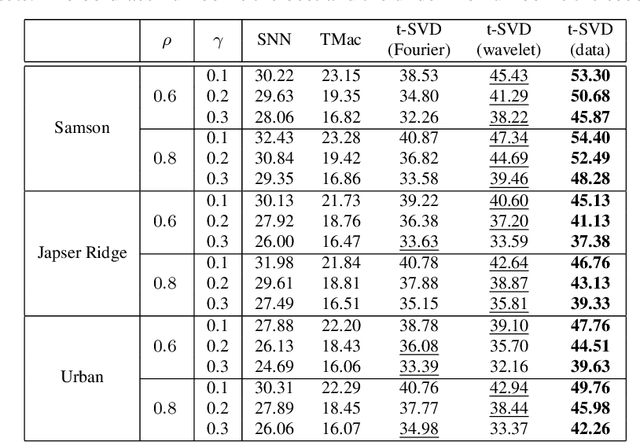
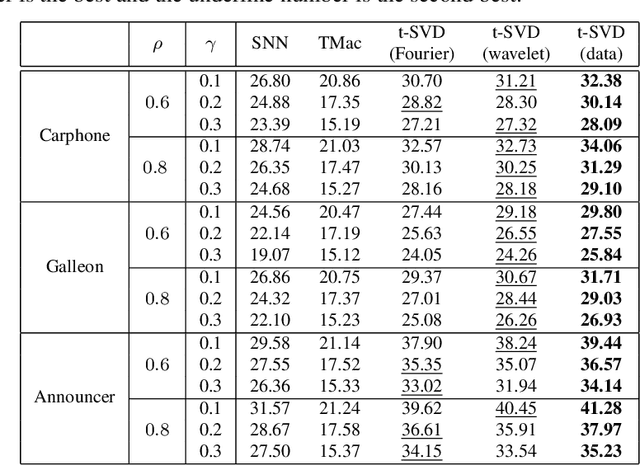
In this paper, we study robust tensor completion by using transformed tensor singular value decomposition (SVD), which employs unitary transform matrices instead of discrete Fourier transform matrix that is used in the traditional tensor SVD. The main motivation is that a lower tubal rank tensor can be obtained by using other unitary transform matrices than that by using discrete Fourier transform matrix. This would be more effective for robust tensor completion. Experimental results for hyperspectral, video and face datasets have shown that the recovery performance for the robust tensor completion problem by using transformed tensor SVD is better in PSNR than that by using Fourier transform and other robust tensor completion methods.