Low-Rank Tensor Learning by Generalized Nonconvex Regularization

In this paper, we study the problem of low-rank tensor learning, where only a few of training samples are observed and the underlying tensor has a low-rank structure. The existing methods are based on the sum of nuclear norms of unfolding matrices of a tensor, which may be suboptimal. In order to explore the low-rankness of the underlying tensor effectively, we propose a nonconvex model based on transformed tensor nuclear norm for low-rank tensor learning. Specifically, a family of nonconvex functions are employed onto the singular values of all frontal slices of a tensor in the transformed domain to characterize the low-rankness of the underlying tensor. An error bound between the stationary point of the nonconvex model and the underlying tensor is established under restricted strong convexity on the loss function (such as least squares loss and logistic regression) and suitable regularity conditions on the nonconvex penalty function. By reformulating the nonconvex function into the difference of two convex functions, a proximal majorization-minimization (PMM) algorithm is designed to solve the resulting model. Then the global convergence and convergence rate of PMM are established under very mild conditions. Numerical experiments are conducted on tensor completion and binary classification to demonstrate the effectiveness of the proposed method over other state-of-the-art methods.

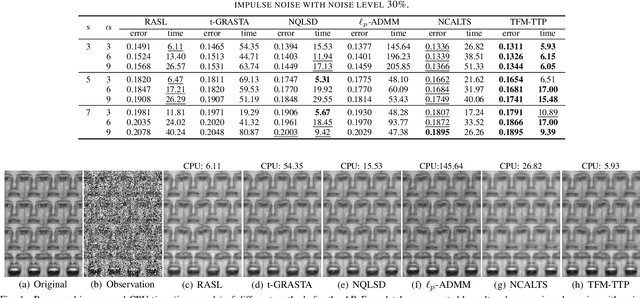
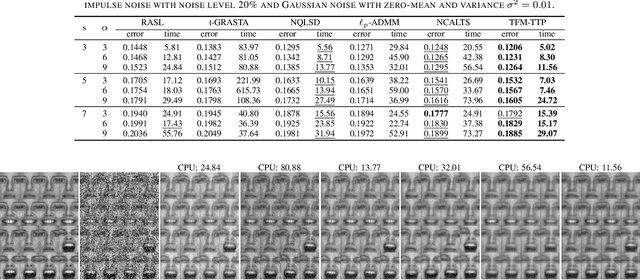
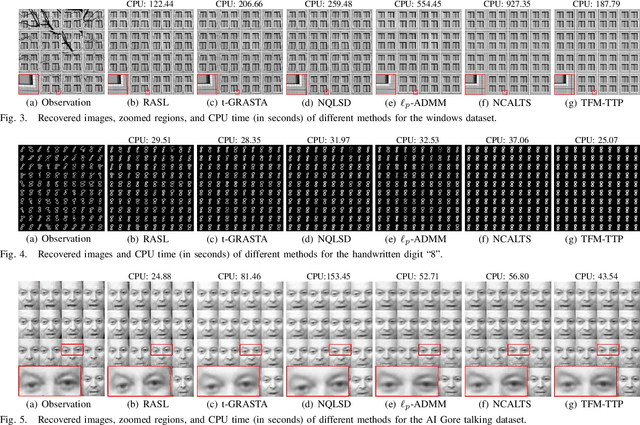
Tensor Factorization via Transformed Tensor-Tensor Product for Image Alignment

In this paper, we study the problem of a batch of linearly correlated image alignment, where the observed images are deformed by some unknown domain transformations, and corrupted by additive Gaussian noise and sparse noise simultaneously. By stacking these images as the frontal slices of a third-order tensor, we propose to utilize the tensor factorization method via transformed tensor-tensor product to explore the low-rankness of the underlying tensor, which is factorized into the product of two smaller tensors via transformed tensor-tensor product under any unitary transformation. The main advantage of transformed tensor-tensor product is that its computational complexity is lower compared with the existing literature based on transformed tensor nuclear norm. Moreover, the tensor $\ell_p$ $(0<p<1)$ norm is employed to characterize the sparsity of sparse noise and the tensor Frobenius norm is adopted to model additive Gaussian noise. A generalized Gauss-Newton algorithm is designed to solve the resulting model by linearizing the domain transformations and a proximal Gauss-Seidel algorithm is developed to solve the corresponding subproblem. Furthermore, the convergence of the proximal Gauss-Seidel algorithm is established, whose convergence rate is also analyzed based on the Kurdyka-$\L$ojasiewicz property. Extensive numerical experiments on real-world image datasets are carried out to demonstrate the superior performance of the proposed method as compared to several state-of-the-art methods in both accuracy and computational time.

Sparse Nonnegative Tucker Decomposition and Completion under Noisy Observations

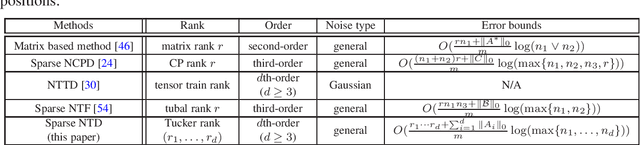
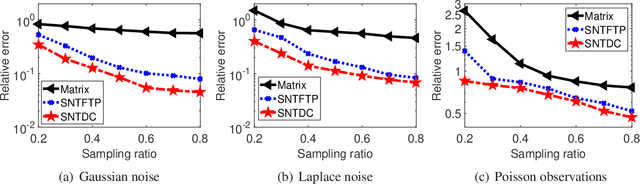
Tensor decomposition is a powerful tool for extracting physically meaningful latent factors from multi-dimensional nonnegative data, and has been an increasing interest in a variety of fields such as image processing, machine learning, and computer vision. In this paper, we propose a sparse nonnegative Tucker decomposition and completion method for the recovery of underlying nonnegative data under noisy observations. Here the underlying nonnegative data tensor is decomposed into a core tensor and several factor matrices with all entries being nonnegative and the factor matrices being sparse. The loss function is derived by the maximum likelihood estimation of the noisy observations, and the $\ell_0$ norm is employed to enhance the sparsity of the factor matrices. We establish the error bound of the estimator of the proposed model under generic noise scenarios, which is then specified to the observations with additive Gaussian noise, additive Laplace noise, and Poisson observations, respectively. Our theoretical results are better than those by existing tensor-based or matrix-based methods. Moreover, the minimax lower bounds are shown to be matched with the derived upper bounds up to logarithmic factors. Numerical examples on both synthetic and real-world data sets demonstrate the superiority of the proposed method for nonnegative tensor data completion.

On $O )$ Sample Entries for $n_1 \times n_2 \times n_3$ Tensor Completion via Unitary Transformation

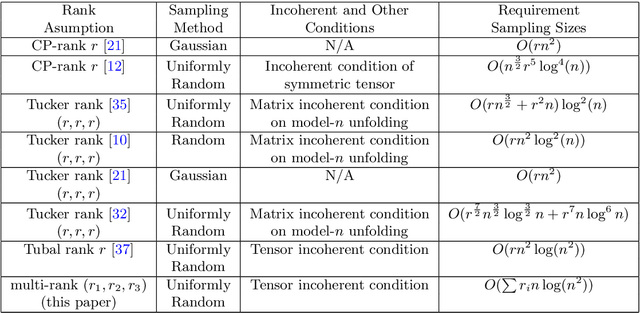
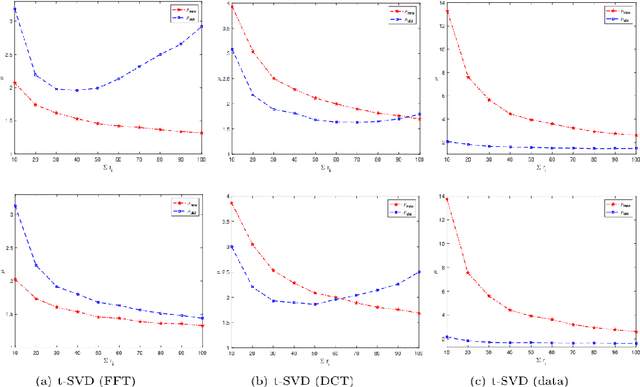
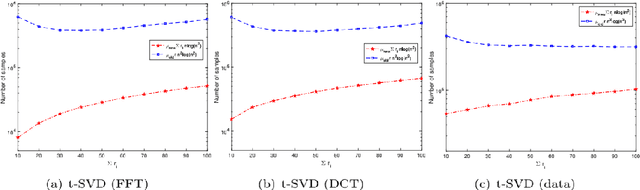
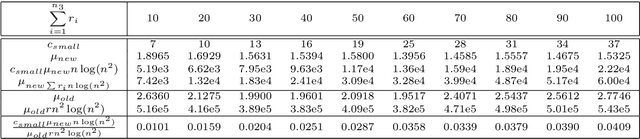
One of the key problems in tensor completion is the number of uniformly random sample entries required for recovery guarantee. The main aim of this paper is to study $n_1 \times n_2 \times n_3$ third-order tensor completion and investigate into incoherence conditions of $n_3$ low-rank $n_1$-by-$n_2$ matrix slices under the transformed tensor singular value decomposition where the unitary transformation is applied along $n_3$-dimension. We show that such low-rank tensors can be recovered exactly with high probability when the number of randomly observed entries is of order $O( r\max \{n_1, n_2 \} \log ( \max \{ n_1, n_2 \} n_3))$, where $r$ is the sum of the ranks of these $n_3$ matrix slices in the transformed tensor. By utilizing synthetic data and imaging data sets, we demonstrate that the theoretical result can be obtained under valid incoherence conditions, and the tensor completion performance of the proposed method is also better than that of existing methods in terms of sample sizes requirement.

Sparse Nonnegative Tensor Factorization and Completion with Noisy Observations

In this paper, we study the sparse nonnegative tensor factorization and completion problem from partial and noisy observations for third-order tensors. Because of sparsity and nonnegativity, the underling tensor is decomposed into the tensor-tensor product of one sparse nonnegative tensor and one nonnegative tensor. We propose to minimize the sum of the maximum likelihood estimate for the observations with nonnegativity constraints and the tensor $\ell_0$ norm for the sparse factor. We show that the error bounds of the estimator of the proposed model can be established under general noise observations. The detailed error bounds under specific noise distributions including additive Gaussian noise, additive Laplace noise, and Poisson observations can be derived. Moreover, the minimax lower bounds are shown to be matched with the established upper bounds up to a logarithmic factor of the sizes of the underlying tensor. These theoretical results for tensors are better than those obtained for matrices, and this illustrates the advantage of the use of nonnegative sparse tensor models for completion and denoising. Numerical experiments are provided to validate the superiority of the proposed tensor-based method compared with the matrix-based approach.

Orthogonal Nonnegative Tucker Decomposition

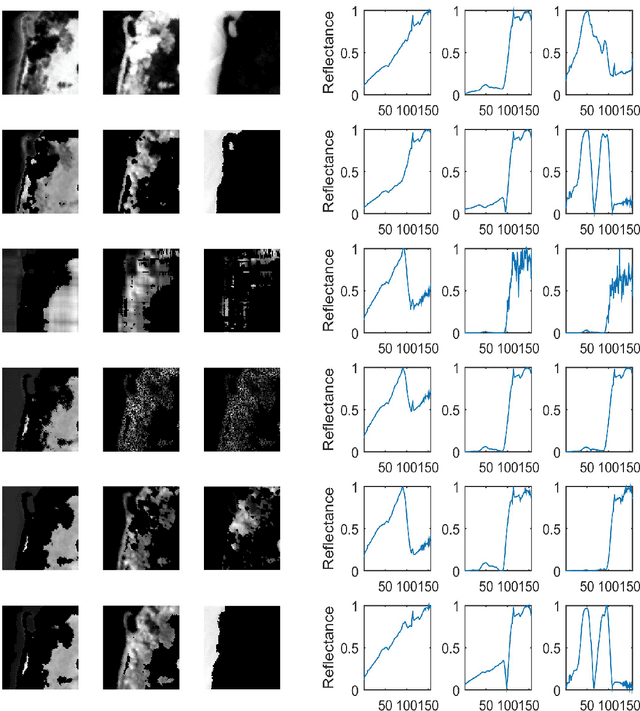
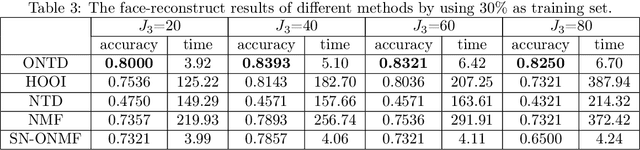
In this paper, we study the nonnegative tensor data and propose an orthogonal nonnegative Tucker decomposition (ONTD). We discuss some properties of ONTD and develop a convex relaxation algorithm of the augmented Lagrangian function to solve the optimization problem. The convergence of the algorithm is given. We employ ONTD on the image data sets from the real world applications including face recognition, image representation, hyperspectral unmixing. Numerical results are shown to illustrate the effectiveness of the proposed algorithm.

Robust Tensor Completion Using Transformed Tensor SVD

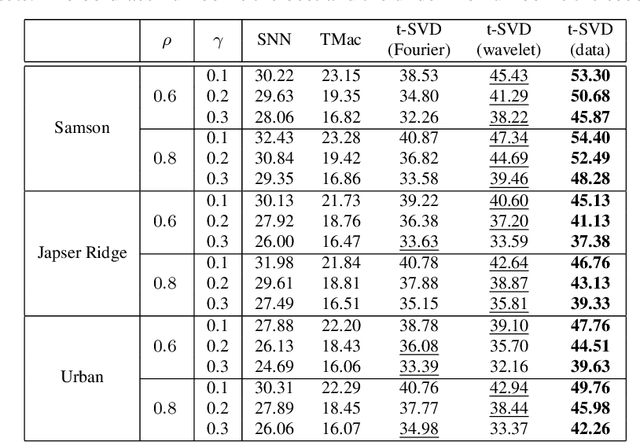
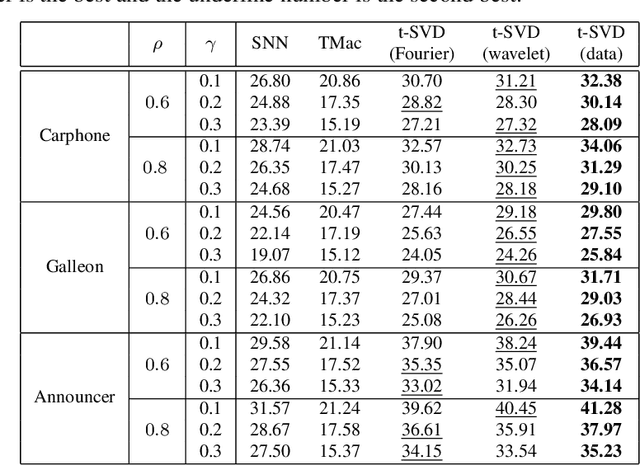
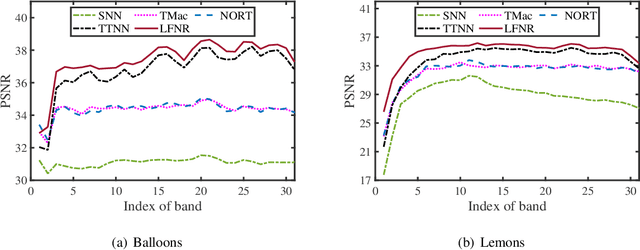
In this paper, we study robust tensor completion by using transformed tensor singular value decomposition (SVD), which employs unitary transform matrices instead of discrete Fourier transform matrix that is used in the traditional tensor SVD. The main motivation is that a lower tubal rank tensor can be obtained by using other unitary transform matrices than that by using discrete Fourier transform matrix. This would be more effective for robust tensor completion. Experimental results for hyperspectral, video and face datasets have shown that the recovery performance for the robust tensor completion problem by using transformed tensor SVD is better in PSNR than that by using Fourier transform and other robust tensor completion methods.