Sparse Tucker Decomposition and Graph Regularization for High-Dimensional Time Series Forecasting

Existing methods of vector autoregressive model for multivariate time series analysis make use of low-rank matrix approximation or Tucker decomposition to reduce the dimension of the over-parameterization issue. In this paper, we propose a sparse Tucker decomposition method with graph regularization for high-dimensional vector autoregressive time series. By stacking the time-series transition matrices into a third-order tensor, the sparse Tucker decomposition is employed to characterize important interactions within the transition third-order tensor and reduce the number of parameters. Moreover, the graph regularization is employed to measure the local consistency of the response, predictor and temporal factor matrices in the vector autoregressive model.The two proposed regularization techniques can be shown to more accurate parameters estimation. A non-asymptotic error bound of the estimator of the proposed method is established, which is lower than those of the existing matrix or tensor based methods. A proximal alternating linearized minimization algorithm is designed to solve the resulting model and its global convergence is established under very mild conditions. Extensive numerical experiments on synthetic data and real-world datasets are carried out to verify the superior performance of the proposed method over existing state-of-the-art methods.

Low-Rank Tensor Learning by Generalized Nonconvex Regularization

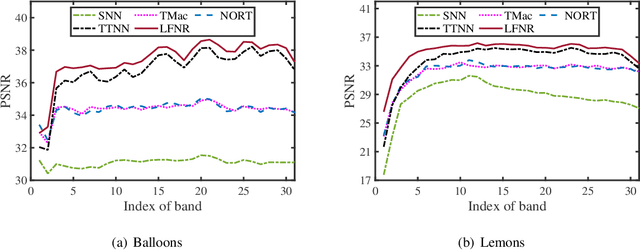
In this paper, we study the problem of low-rank tensor learning, where only a few of training samples are observed and the underlying tensor has a low-rank structure. The existing methods are based on the sum of nuclear norms of unfolding matrices of a tensor, which may be suboptimal. In order to explore the low-rankness of the underlying tensor effectively, we propose a nonconvex model based on transformed tensor nuclear norm for low-rank tensor learning. Specifically, a family of nonconvex functions are employed onto the singular values of all frontal slices of a tensor in the transformed domain to characterize the low-rankness of the underlying tensor. An error bound between the stationary point of the nonconvex model and the underlying tensor is established under restricted strong convexity on the loss function (such as least squares loss and logistic regression) and suitable regularity conditions on the nonconvex penalty function. By reformulating the nonconvex function into the difference of two convex functions, a proximal majorization-minimization (PMM) algorithm is designed to solve the resulting model. Then the global convergence and convergence rate of PMM are established under very mild conditions. Numerical experiments are conducted on tensor completion and binary classification to demonstrate the effectiveness of the proposed method over other state-of-the-art methods.

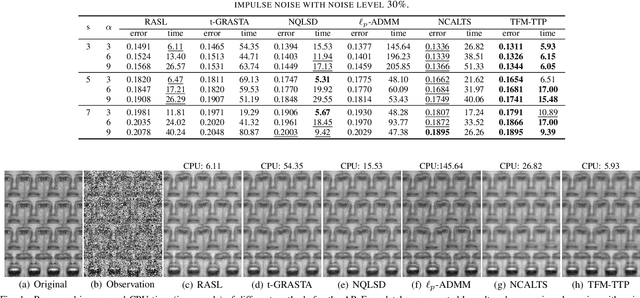
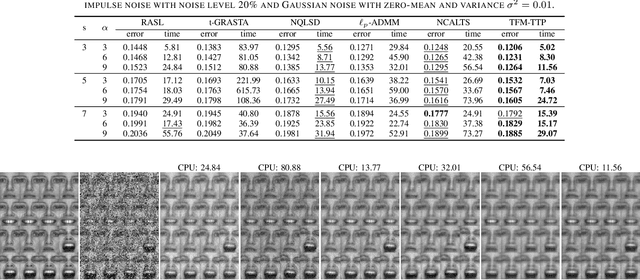
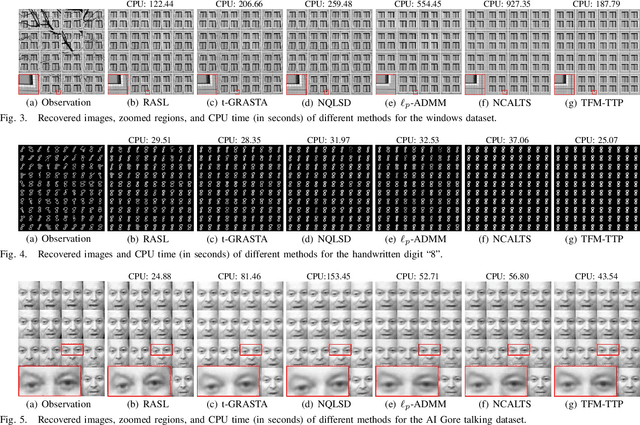
Tensor Factorization via Transformed Tensor-Tensor Product for Image Alignment

In this paper, we study the problem of a batch of linearly correlated image alignment, where the observed images are deformed by some unknown domain transformations, and corrupted by additive Gaussian noise and sparse noise simultaneously. By stacking these images as the frontal slices of a third-order tensor, we propose to utilize the tensor factorization method via transformed tensor-tensor product to explore the low-rankness of the underlying tensor, which is factorized into the product of two smaller tensors via transformed tensor-tensor product under any unitary transformation. The main advantage of transformed tensor-tensor product is that its computational complexity is lower compared with the existing literature based on transformed tensor nuclear norm. Moreover, the tensor $\ell_p$ $(0<p<1)$ norm is employed to characterize the sparsity of sparse noise and the tensor Frobenius norm is adopted to model additive Gaussian noise. A generalized Gauss-Newton algorithm is designed to solve the resulting model by linearizing the domain transformations and a proximal Gauss-Seidel algorithm is developed to solve the corresponding subproblem. Furthermore, the convergence of the proximal Gauss-Seidel algorithm is established, whose convergence rate is also analyzed based on the Kurdyka-$\L$ojasiewicz property. Extensive numerical experiments on real-world image datasets are carried out to demonstrate the superior performance of the proposed method as compared to several state-of-the-art methods in both accuracy and computational time.