Low-Rank Tensor Learning by Generalized Nonconvex Regularization
Paper and Code
Oct 24, 2024
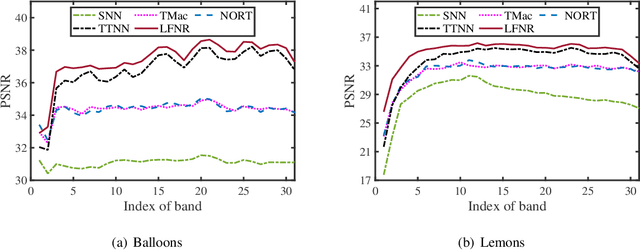


In this paper, we study the problem of low-rank tensor learning, where only a few of training samples are observed and the underlying tensor has a low-rank structure. The existing methods are based on the sum of nuclear norms of unfolding matrices of a tensor, which may be suboptimal. In order to explore the low-rankness of the underlying tensor effectively, we propose a nonconvex model based on transformed tensor nuclear norm for low-rank tensor learning. Specifically, a family of nonconvex functions are employed onto the singular values of all frontal slices of a tensor in the transformed domain to characterize the low-rankness of the underlying tensor. An error bound between the stationary point of the nonconvex model and the underlying tensor is established under restricted strong convexity on the loss function (such as least squares loss and logistic regression) and suitable regularity conditions on the nonconvex penalty function. By reformulating the nonconvex function into the difference of two convex functions, a proximal majorization-minimization (PMM) algorithm is designed to solve the resulting model. Then the global convergence and convergence rate of PMM are established under very mild conditions. Numerical experiments are conducted on tensor completion and binary classification to demonstrate the effectiveness of the proposed method over other state-of-the-art methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge