Fully-Connected Tensor Network Decomposition for Robust Tensor Completion Problem

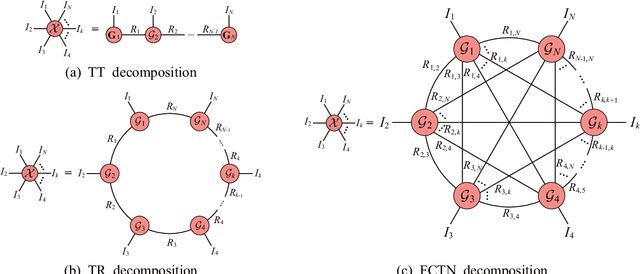
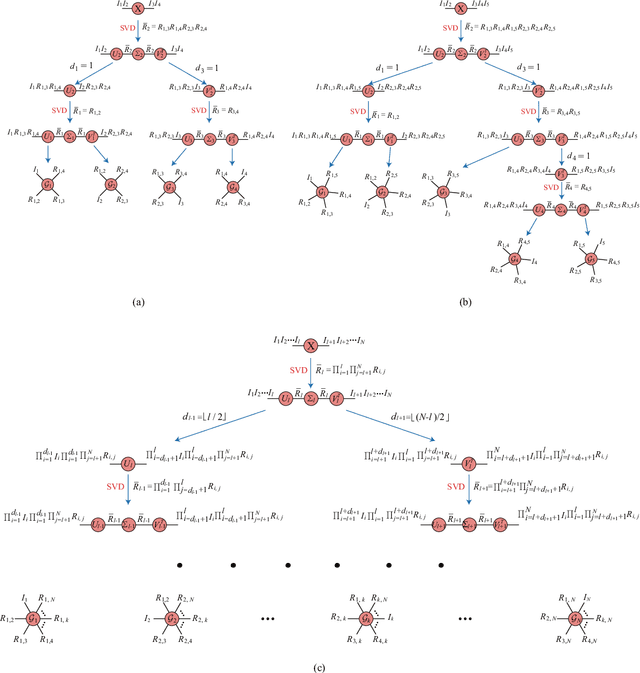
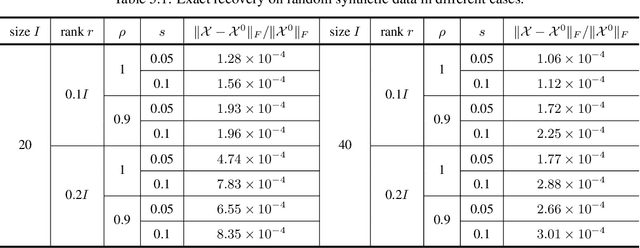
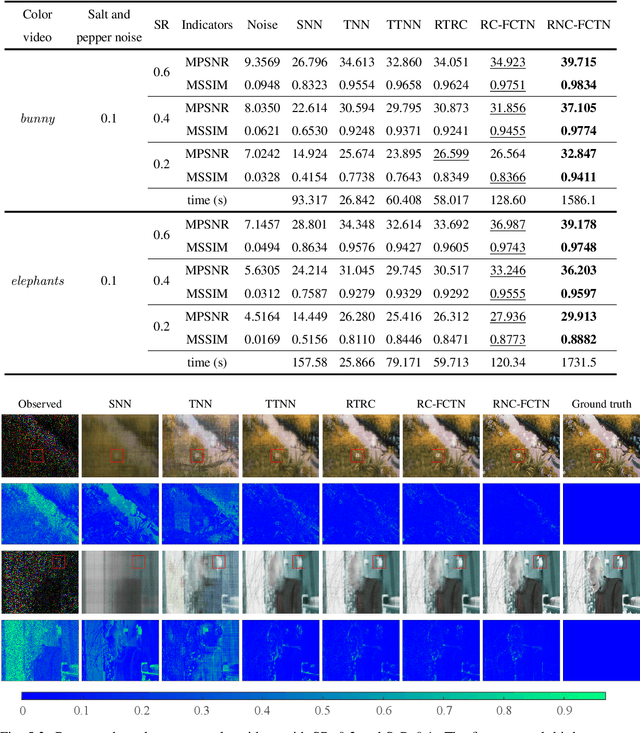
The robust tensor completion (RTC) problem, which aims to reconstruct a low-rank tensor from partially observed tensor contaminated by a sparse tensor, has received increasing attention. In this paper, by leveraging the superior expression of the fully-connected tensor network (FCTN) decomposition, we propose a $\textbf{FCTN}$-based $\textbf{r}$obust $\textbf{c}$onvex optimization model (RC-FCTN) for the RTC problem. Then, we rigorously establish the exact recovery guarantee for the RC-FCTN. For solving the constrained optimization model RC-FCTN, we develop an alternating direction method of multipliers (ADMM)-based algorithm, which enjoys the global convergence guarantee. Moreover, we suggest a $\textbf{FCTN}$-based $\textbf{r}$obust $\textbf{n}$on$\textbf{c}$onvex optimization model (RNC-FCTN) for the RTC problem. A proximal alternating minimization (PAM)-based algorithm is developed to solve the proposed RNC-FCTN. Meanwhile, we theoretically derive the convergence of the PAM-based algorithm. Comprehensive numerical experiments in several applications, such as video completion and video background subtraction, demonstrate that proposed methods are superior to several state-of-the-art methods.

On $O )$ Sample Entries for $n_1 \times n_2 \times n_3$ Tensor Completion via Unitary Transformation

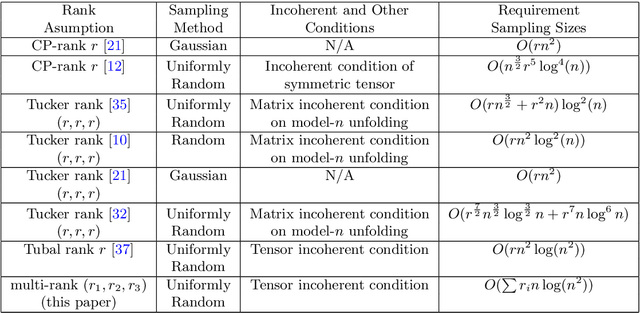
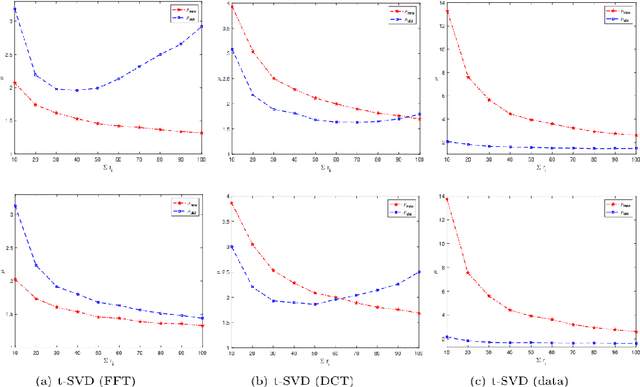
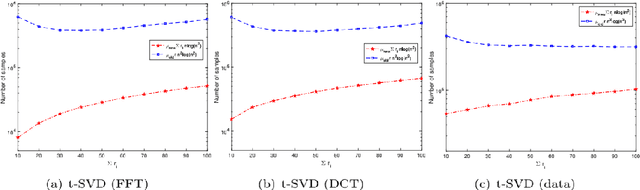
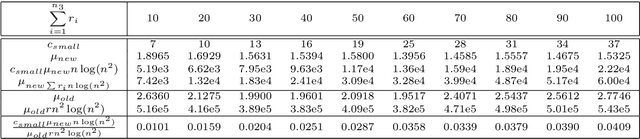
One of the key problems in tensor completion is the number of uniformly random sample entries required for recovery guarantee. The main aim of this paper is to study $n_1 \times n_2 \times n_3$ third-order tensor completion and investigate into incoherence conditions of $n_3$ low-rank $n_1$-by-$n_2$ matrix slices under the transformed tensor singular value decomposition where the unitary transformation is applied along $n_3$-dimension. We show that such low-rank tensors can be recovered exactly with high probability when the number of randomly observed entries is of order $O( r\max \{n_1, n_2 \} \log ( \max \{ n_1, n_2 \} n_3))$, where $r$ is the sum of the ranks of these $n_3$ matrix slices in the transformed tensor. By utilizing synthetic data and imaging data sets, we demonstrate that the theoretical result can be obtained under valid incoherence conditions, and the tensor completion performance of the proposed method is also better than that of existing methods in terms of sample sizes requirement.