Ting-Zhu Huang
A Knowledge-driven Adaptive Collaboration of LLMs for Enhancing Medical Decision-making
Sep 18, 2025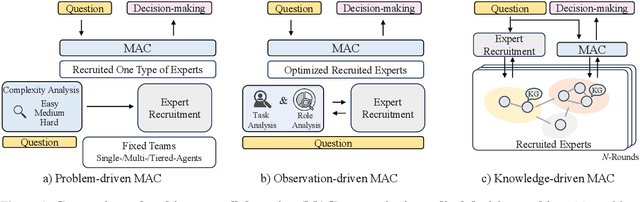
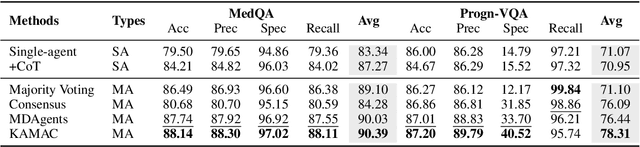
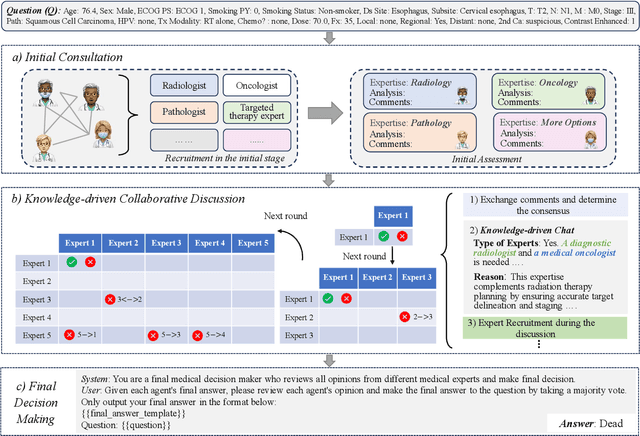
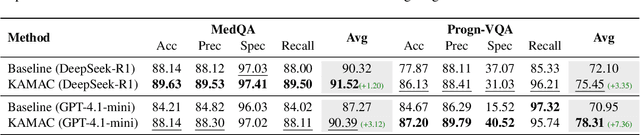
Abstract:Medical decision-making often involves integrating knowledge from multiple clinical specialties, typically achieved through multidisciplinary teams. Inspired by this collaborative process, recent work has leveraged large language models (LLMs) in multi-agent collaboration frameworks to emulate expert teamwork. While these approaches improve reasoning through agent interaction, they are limited by static, pre-assigned roles, which hinder adaptability and dynamic knowledge integration. To address these limitations, we propose KAMAC, a Knowledge-driven Adaptive Multi-Agent Collaboration framework that enables LLM agents to dynamically form and expand expert teams based on the evolving diagnostic context. KAMAC begins with one or more expert agents and then conducts a knowledge-driven discussion to identify and fill knowledge gaps by recruiting additional specialists as needed. This supports flexible, scalable collaboration in complex clinical scenarios, with decisions finalized through reviewing updated agent comments. Experiments on two real-world medical benchmarks demonstrate that KAMAC significantly outperforms both single-agent and advanced multi-agent methods, particularly in complex clinical scenarios (i.e., cancer prognosis) requiring dynamic, cross-specialty expertise. Our code is publicly available at: https://github.com/XiaoXiao-Woo/KAMAC.
SVDinsTN: An Integrated Method for Tensor Network Representation with Efficient Structure Search
May 24, 2023

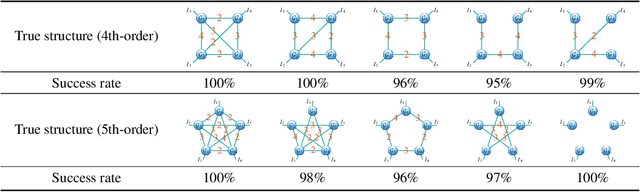
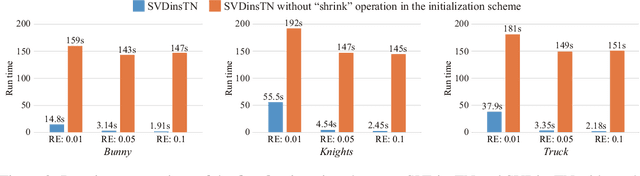
Abstract:Tensor network (TN) representation is a powerful technique for data analysis and machine learning. It practically involves a challenging TN structure search (TN-SS) problem, which aims to search for the optimal structure to achieve a compact representation. Existing TN-SS methods mainly adopt a bi-level optimization method that leads to excessive computational costs due to repeated structure evaluations. To address this issue, we propose an efficient integrated (single-level) method named SVD-inspired TN decomposition (SVDinsTN), eliminating the need for repeated tedious structure evaluation. By inserting a diagonal factor for each edge of the fully-connected TN, we calculate TN cores and diagonal factors simultaneously, with factor sparsity revealing the most compact TN structure. Experimental results on real-world data demonstrate that SVDinsTN achieves approximately $10^2\sim{}10^3$ times acceleration in runtime compared to the existing TN-SS methods while maintaining a comparable level of representation ability.
CD-GAN: a robust fusion-based generative adversarial network for unsupervised change detection between heterogeneous images
Mar 02, 2022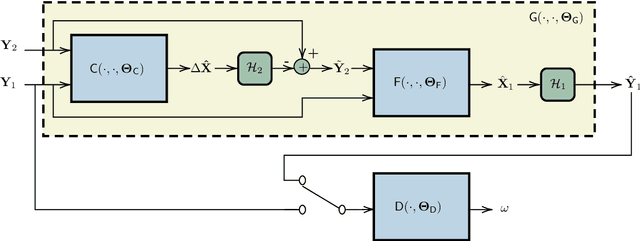
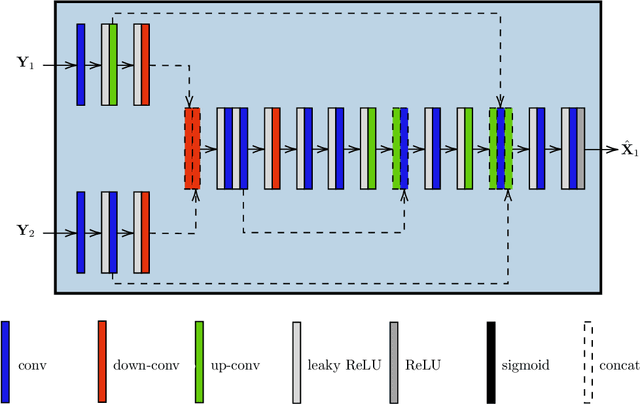

Abstract:In the context of Earth observation, the detection of changes is performed from multitemporal images acquired by sensors with possibly different characteristics and modalities. Even when restricting to the optical modality, this task has proved to be challenging as soon as the sensors provide images of different spatial and/or spectral resolutions. This paper proposes a novel unsupervised change detection method dedicated to such so-called heterogeneous optical images. This method capitalizes on recent advances which frame the change detection problem into a robust fusion framework. More precisely, we show that a deep adversarial network designed and trained beforehand to fuse a pair of multiband images can be easily complemented by a network with the same architecture to perform change detection. The resulting overall architecture itself follows an adversarial strategy where the fusion network and the additional network are interpreted as essential building blocks of a generator. A comparison with state-of-the-art change detection methods demonstrate the versatility and the effectiveness of the proposed approach.
A Triple-Double Convolutional Neural Network for Panchromatic Sharpening
Dec 04, 2021
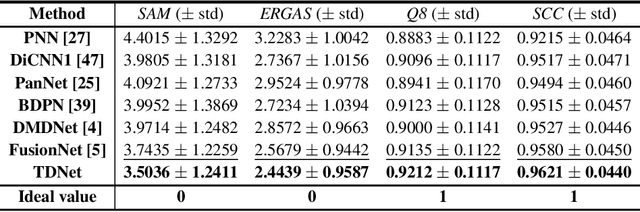
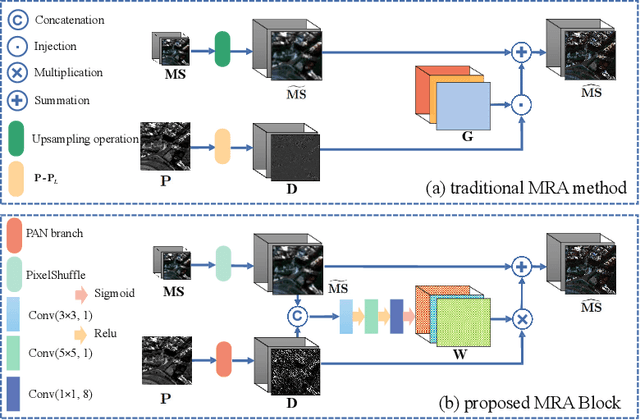
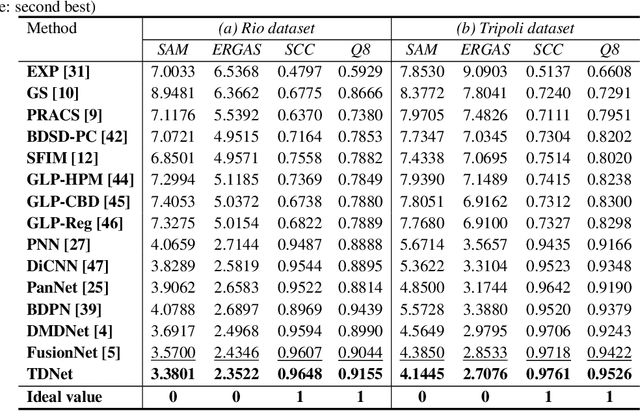
Abstract:Pansharpening refers to the fusion of a panchromatic image with a high spatial resolution and a multispectral image with a low spatial resolution, aiming to obtain a high spatial resolution multispectral image. In this paper, we propose a novel deep neural network architecture with level-domain based loss function for pansharpening by taking into account the following double-type structures, \emph{i.e.,} double-level, double-branch, and double-direction, called as triple-double network (TDNet). By using the structure of TDNet, the spatial details of the panchromatic image can be fully exploited and utilized to progressively inject into the low spatial resolution multispectral image, thus yielding the high spatial resolution output. The specific network design is motivated by the physical formula of the traditional multi-resolution analysis (MRA) methods. Hence, an effective MRA fusion module is also integrated into the TDNet. Besides, we adopt a few ResNet blocks and some multi-scale convolution kernels to deepen and widen the network to effectively enhance the feature extraction and the robustness of the proposed TDNet. Extensive experiments on reduced- and full-resolution datasets acquired by WorldView-3, QuickBird, and GaoFen-2 sensors demonstrate the superiority of the proposed TDNet compared with some recent state-of-the-art pansharpening approaches. An ablation study has also corroborated the effectiveness of the proposed approach.
Nonlinear Transform Induced Tensor Nuclear Norm for Tensor Completion
Oct 17, 2021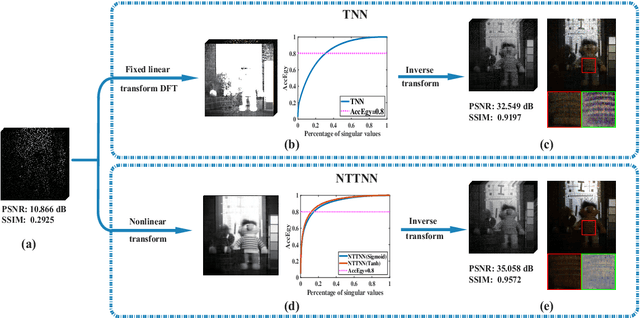

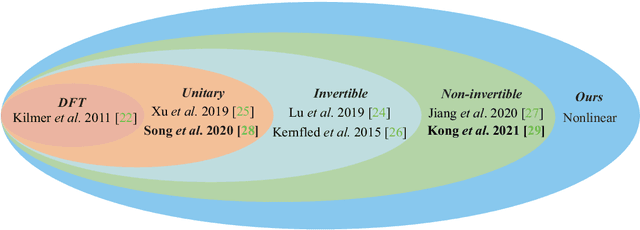
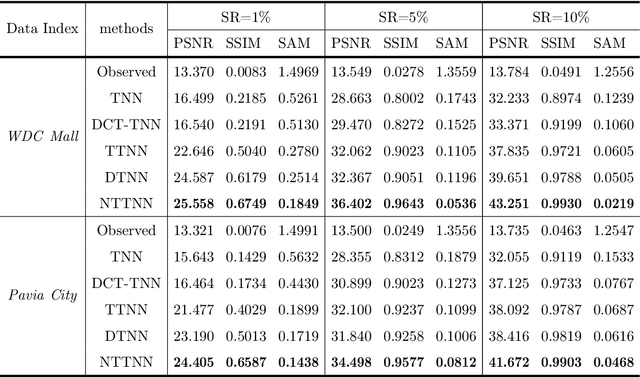
Abstract:The linear transform-based tensor nuclear norm (TNN) methods have recently obtained promising results for tensor completion. The main idea of this type of methods is exploiting the low-rank structure of frontal slices of the targeted tensor under the linear transform along the third mode. However, the low-rankness of frontal slices is not significant under linear transforms family. To better pursue the low-rank approximation, we propose a nonlinear transform-based TNN (NTTNN). More concretely, the proposed nonlinear transform is a composite transform consisting of the linear semi-orthogonal transform along the third mode and the element-wise nonlinear transform on frontal slices of the tensor under the linear semi-orthogonal transform, which are indispensable and complementary in the composite transform to fully exploit the underlying low-rankness. Based on the suggested low-rankness metric, i.e., NTTNN, we propose a low-rank tensor completion (LRTC) model. To tackle the resulting nonlinear and nonconvex optimization model, we elaborately design the proximal alternating minimization (PAM) algorithm and establish the theoretical convergence guarantee of the PAM algorithm. Extensive experimental results on hyperspectral images, multispectral images, and videos show that the our method outperforms linear transform-based state-of-the-art LRTC methods qualitatively and quantitatively.
Fully-Connected Tensor Network Decomposition for Robust Tensor Completion Problem
Oct 17, 2021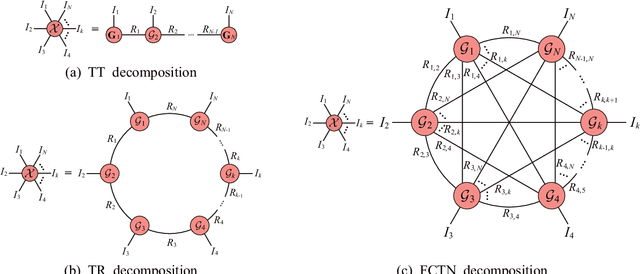
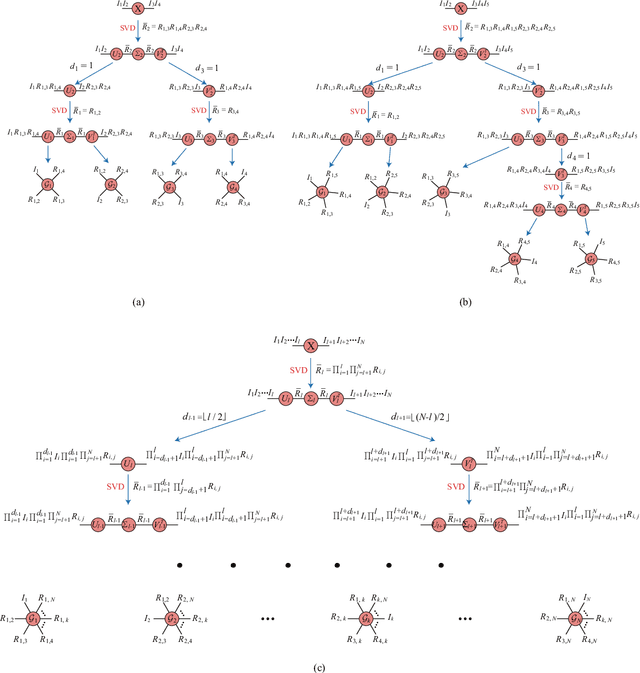
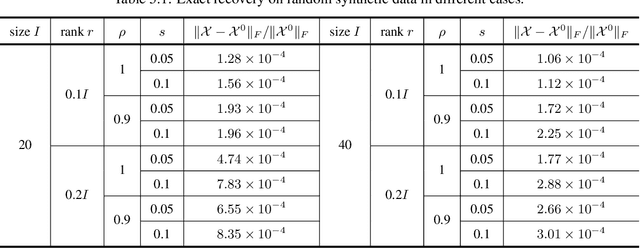
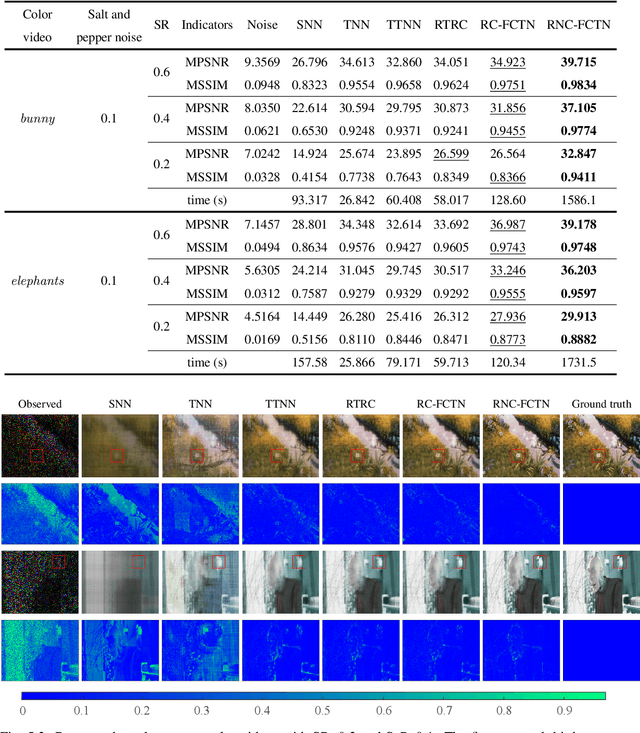
Abstract:The robust tensor completion (RTC) problem, which aims to reconstruct a low-rank tensor from partially observed tensor contaminated by a sparse tensor, has received increasing attention. In this paper, by leveraging the superior expression of the fully-connected tensor network (FCTN) decomposition, we propose a $\textbf{FCTN}$-based $\textbf{r}$obust $\textbf{c}$onvex optimization model (RC-FCTN) for the RTC problem. Then, we rigorously establish the exact recovery guarantee for the RC-FCTN. For solving the constrained optimization model RC-FCTN, we develop an alternating direction method of multipliers (ADMM)-based algorithm, which enjoys the global convergence guarantee. Moreover, we suggest a $\textbf{FCTN}$-based $\textbf{r}$obust $\textbf{n}$on$\textbf{c}$onvex optimization model (RNC-FCTN) for the RTC problem. A proximal alternating minimization (PAM)-based algorithm is developed to solve the proposed RNC-FCTN. Meanwhile, we theoretically derive the convergence of the PAM-based algorithm. Comprehensive numerical experiments in several applications, such as video completion and video background subtraction, demonstrate that proposed methods are superior to several state-of-the-art methods.
Fusformer: A Transformer-based Fusion Approach for Hyperspectral Image Super-resolution
Sep 05, 2021



Abstract:Hyperspectral image has become increasingly crucial due to its abundant spectral information. However, It has poor spatial resolution with the limitation of the current imaging mechanism. Nowadays, many convolutional neural networks have been proposed for the hyperspectral image super-resolution problem. However, convolutional neural network (CNN) based methods only consider the local information instead of the global one with the limited kernel size of receptive field in the convolution operation. In this paper, we design a network based on the transformer for fusing the low-resolution hyperspectral images and high-resolution multispectral images to obtain the high-resolution hyperspectral images. Thanks to the representing ability of the transformer, our approach is able to explore the intrinsic relationships of features globally. Furthermore, considering the LR-HSIs hold the main spectral structure, the network focuses on the spatial detail estimation releasing from the burden of reconstructing the whole data. It reduces the mapping space of the proposed network, which enhances the final performance. Various experiments and quality indexes show our approach's superiority compared with other state-of-the-art methods.
Hyperspectral Image Super-resolution via Deep Spatio-spectral Convolutional Neural Networks
May 29, 2020



Abstract:Hyperspectral images are of crucial importance in order to better understand features of different materials. To reach this goal, they leverage on a high number of spectral bands. However, this interesting characteristic is often paid by a reduced spatial resolution compared with traditional multispectral image systems. In order to alleviate this issue, in this work, we propose a simple and efficient architecture for deep convolutional neural networks to fuse a low-resolution hyperspectral image (LR-HSI) and a high-resolution multispectral image (HR-MSI), yielding a high-resolution hyperspectral image (HR-HSI). The network is designed to preserve both spatial and spectral information thanks to an architecture from two folds: one is to utilize the HR-HSI at a different scale to get an output with a satisfied spectral preservation; another one is to apply concepts of multi-resolution analysis to extract high-frequency information, aiming to output high quality spatial details. Finally, a plain mean squared error loss function is used to measure the performance during the training. Extensive experiments demonstrate that the proposed network architecture achieves best performance (both qualitatively and quantitatively) compared with recent state-of-the-art hyperspectral image super-resolution approaches. Moreover, other significant advantages can be pointed out by the use of the proposed approach, such as, a better network generalization ability, a limited computational burden, and a robustness with respect to the number of training samples.
Tensor completion via nonconvex tensor ring rank minimization with guaranteed convergence
May 14, 2020



Abstract:In recent studies, the tensor ring (TR) rank has shown high effectiveness in tensor completion due to its ability of capturing the intrinsic structure within high-order tensors. A recently proposed TR rank minimization method is based on the convex relaxation by penalizing the weighted sum of nuclear norm of TR unfolding matrices. However, this method treats each singular value equally and neglects their physical meanings, which usually leads to suboptimal solutions in practice. In this paper, we propose to use the logdet-based function as a nonconvex smooth relaxation of the TR rank for tensor completion, which can more accurately approximate the TR rank and better promote the low-rankness of the solution. To solve the proposed nonconvex model efficiently, we develop an alternating direction method of multipliers algorithm and theoretically prove that, under some mild assumptions, our algorithm converges to a stationary point. Extensive experiments on color images, multispectral images, and color videos demonstrate that the proposed method outperforms several state-of-the-art competitors in both visual and quantitative comparison. Key words: nonconvex optimization, tensor ring rank, logdet function, tensor completion, alternating direction method of multipliers.
Tensor train rank minimization with nonlocal self-similarity for tensor completion
Apr 29, 2020



Abstract:The tensor train (TT) rank has received increasing attention in tensor completion due to its ability to capture the global correlation of high-order tensors ($\textrm{order} >3$). For third order visual data, direct TT rank minimization has not exploited the potential of TT rank for high-order tensors. The TT rank minimization accompany with \emph{ket augmentation}, which transforms a lower-order tensor (e.g., visual data) into a higher-order tensor, suffers from serious block-artifacts. To tackle this issue, we suggest the TT rank minimization with nonlocal self-similarity for tensor completion by simultaneously exploring the spatial, temporal/spectral, and nonlocal redundancy in visual data. More precisely, the TT rank minimization is performed on a formed higher-order tensor called group by stacking similar cubes, which naturally and fully takes advantage of the ability of TT rank for high-order tensors. Moreover, the perturbation analysis for the TT low-rankness of each group is established. We develop the alternating direction method of multipliers tailored for the specific structure to solve the proposed model. Extensive experiments demonstrate that the proposed method is superior to several existing state-of-the-art methods in terms of both qualitative and quantitative measures.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge