Nonlinear Transform Induced Tensor Nuclear Norm for Tensor Completion

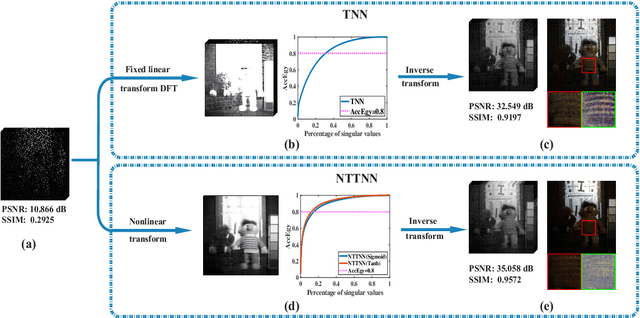
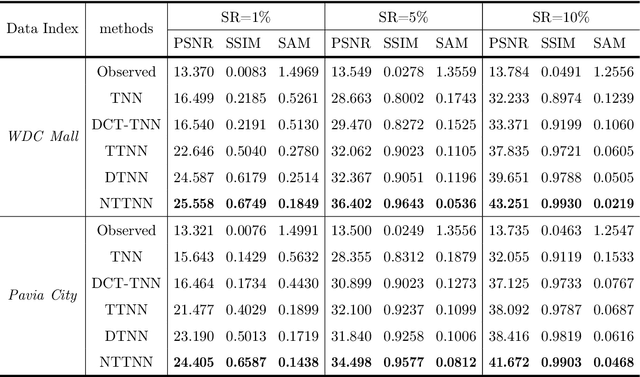
The linear transform-based tensor nuclear norm (TNN) methods have recently obtained promising results for tensor completion. The main idea of this type of methods is exploiting the low-rank structure of frontal slices of the targeted tensor under the linear transform along the third mode. However, the low-rankness of frontal slices is not significant under linear transforms family. To better pursue the low-rank approximation, we propose a nonlinear transform-based TNN (NTTNN). More concretely, the proposed nonlinear transform is a composite transform consisting of the linear semi-orthogonal transform along the third mode and the element-wise nonlinear transform on frontal slices of the tensor under the linear semi-orthogonal transform, which are indispensable and complementary in the composite transform to fully exploit the underlying low-rankness. Based on the suggested low-rankness metric, i.e., NTTNN, we propose a low-rank tensor completion (LRTC) model. To tackle the resulting nonlinear and nonconvex optimization model, we elaborately design the proximal alternating minimization (PAM) algorithm and establish the theoretical convergence guarantee of the PAM algorithm. Extensive experimental results on hyperspectral images, multispectral images, and videos show that the our method outperforms linear transform-based state-of-the-art LRTC methods qualitatively and quantitatively.

Tensor N-tubal rank and its convex relaxation for low-rank tensor recovery

As low-rank modeling has achieved great success in tensor recovery, many research efforts devote to defining the tensor rank. Among them, the recent popular tensor tubal rank, defined based on the tensor singular value decomposition (t-SVD), obtains promising results. However, the framework of the t-SVD and the tensor tubal rank are applicable only to three-way tensors and lack of flexibility to handle different correlations along different modes. To tackle these two issues, we define a new tensor unfolding operator, named mode-$k_1k_2$ tensor unfolding, as the process of lexicographically stacking the mode-$k_1k_2$ slices of an $N$-way tensor into a three-way tensor, which is a three-way extension of the well-known mode-$k$ tensor matricization. Based on it, we define a novel tensor rank, the tensor $N$-tubal rank, as a vector whose elements contain the tubal rank of all mode-$k_1k_2$ unfolding tensors, to depict the correlations along different modes. To efficiently minimize the proposed $N$-tubal rank, we establish its convex relaxation: the weighted sum of tensor nuclear norm (WSTNN). Then, we apply WSTNN to low-rank tensor completion (LRTC) and tensor robust principal component analysis (TRPCA). The corresponding WSTNN-based LRTC and TRPCA models are proposed, and two efficient alternating direction method of multipliers (ADMM)-based algorithms are developed to solve the proposed models. Numerical experiments demonstrate that the proposed models significantly outperform the compared ones.