Ben-Zheng Li
Nonlinear Transform Induced Tensor Nuclear Norm for Tensor Completion
Oct 17, 2021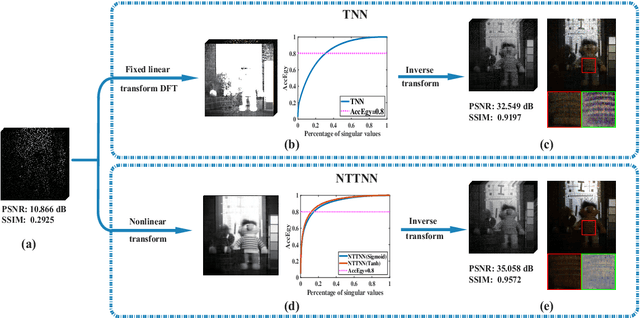

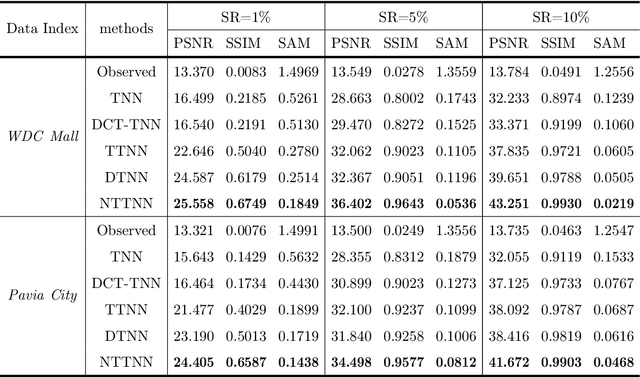
Abstract:The linear transform-based tensor nuclear norm (TNN) methods have recently obtained promising results for tensor completion. The main idea of this type of methods is exploiting the low-rank structure of frontal slices of the targeted tensor under the linear transform along the third mode. However, the low-rankness of frontal slices is not significant under linear transforms family. To better pursue the low-rank approximation, we propose a nonlinear transform-based TNN (NTTNN). More concretely, the proposed nonlinear transform is a composite transform consisting of the linear semi-orthogonal transform along the third mode and the element-wise nonlinear transform on frontal slices of the tensor under the linear semi-orthogonal transform, which are indispensable and complementary in the composite transform to fully exploit the underlying low-rankness. Based on the suggested low-rankness metric, i.e., NTTNN, we propose a low-rank tensor completion (LRTC) model. To tackle the resulting nonlinear and nonconvex optimization model, we elaborately design the proximal alternating minimization (PAM) algorithm and establish the theoretical convergence guarantee of the PAM algorithm. Extensive experimental results on hyperspectral images, multispectral images, and videos show that the our method outperforms linear transform-based state-of-the-art LRTC methods qualitatively and quantitatively.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge