Tensor Star Decomposition

A novel tensor decomposition framework, termed Tensor Star (TS) decomposition, is proposed which represents a new type of tensor network decomposition based on tensor contractions. This is achieved by connecting the core tensors in a ring shape, whereby the core tensors act as skip connections between the factor tensors and allow for direct correlation characterisation between any two arbitrary dimensions. Uniquely, this makes it possible to decompose an order-$N$ tensor into $N$ order-$3$ factor tensors $\{\mathcal{G}_{k}\}_{k=1}^{N}$ and $N$ order-$4$ core tensors $\{\mathcal{C}_{k}\}_{k=1}^{N}$, which are arranged in a star shape. Unlike the class of Tensor Train (TT) decompositions, these factor tensors are not directly connected to one another. The so obtained core tensors also enable consecutive factor tensors to have different latent ranks. In this way, the TS decomposition alleviates the "curse of dimensionality" and controls the "curse of ranks", exhibiting a storage complexity which scales linearly with the number of dimensions and as the fourth power of the ranks.

SVDinsTN: An Integrated Method for Tensor Network Representation with Efficient Structure Search

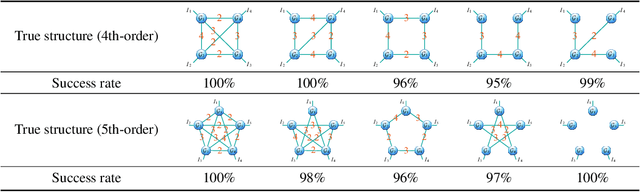
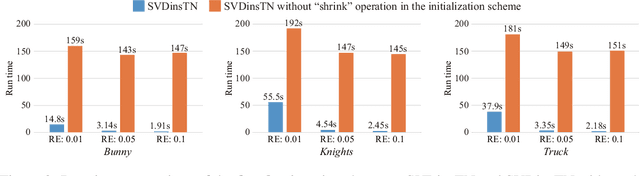
Tensor network (TN) representation is a powerful technique for data analysis and machine learning. It practically involves a challenging TN structure search (TN-SS) problem, which aims to search for the optimal structure to achieve a compact representation. Existing TN-SS methods mainly adopt a bi-level optimization method that leads to excessive computational costs due to repeated structure evaluations. To address this issue, we propose an efficient integrated (single-level) method named SVD-inspired TN decomposition (SVDinsTN), eliminating the need for repeated tedious structure evaluation. By inserting a diagonal factor for each edge of the fully-connected TN, we calculate TN cores and diagonal factors simultaneously, with factor sparsity revealing the most compact TN structure. Experimental results on real-world data demonstrate that SVDinsTN achieves approximately $10^2\sim{}10^3$ times acceleration in runtime compared to the existing TN-SS methods while maintaining a comparable level of representation ability.

Fully-Connected Tensor Network Decomposition for Robust Tensor Completion Problem

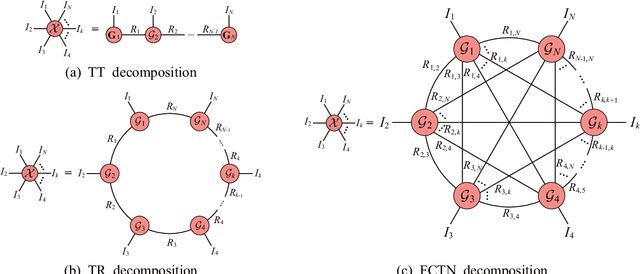
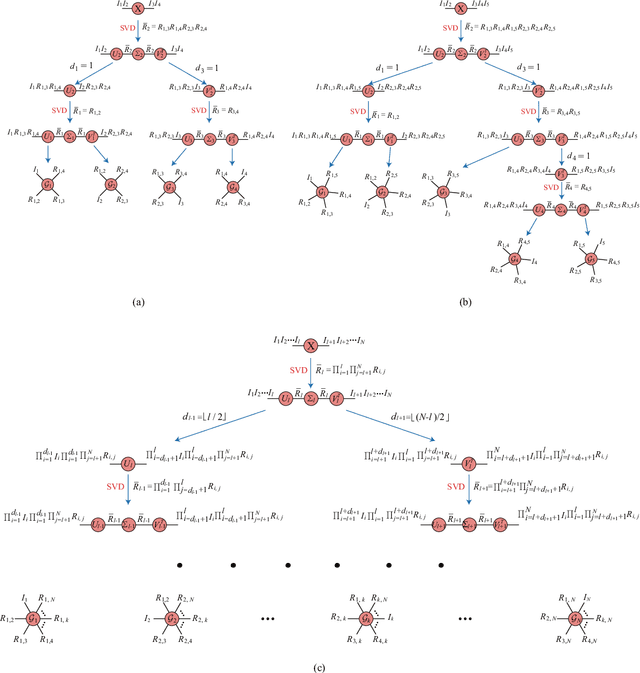
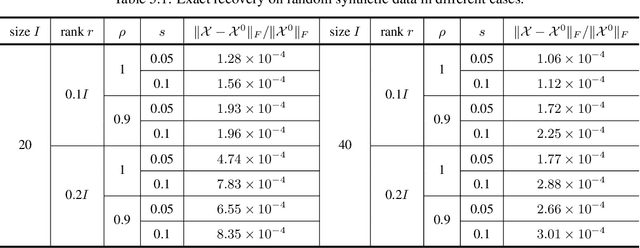
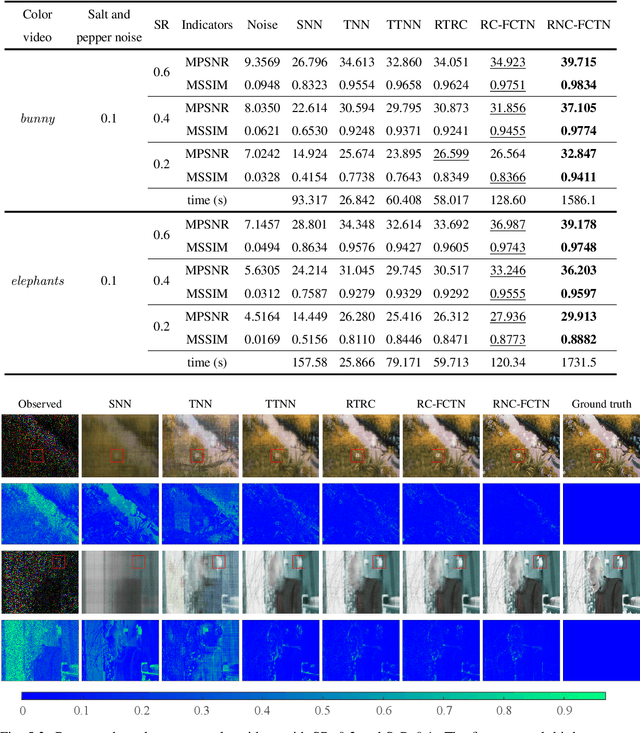
The robust tensor completion (RTC) problem, which aims to reconstruct a low-rank tensor from partially observed tensor contaminated by a sparse tensor, has received increasing attention. In this paper, by leveraging the superior expression of the fully-connected tensor network (FCTN) decomposition, we propose a $\textbf{FCTN}$-based $\textbf{r}$obust $\textbf{c}$onvex optimization model (RC-FCTN) for the RTC problem. Then, we rigorously establish the exact recovery guarantee for the RC-FCTN. For solving the constrained optimization model RC-FCTN, we develop an alternating direction method of multipliers (ADMM)-based algorithm, which enjoys the global convergence guarantee. Moreover, we suggest a $\textbf{FCTN}$-based $\textbf{r}$obust $\textbf{n}$on$\textbf{c}$onvex optimization model (RNC-FCTN) for the RTC problem. A proximal alternating minimization (PAM)-based algorithm is developed to solve the proposed RNC-FCTN. Meanwhile, we theoretically derive the convergence of the PAM-based algorithm. Comprehensive numerical experiments in several applications, such as video completion and video background subtraction, demonstrate that proposed methods are superior to several state-of-the-art methods.

Nonlocal Patch-Based Fully-Connected Tensor Network Decomposition for Remote Sensing Image Inpainting

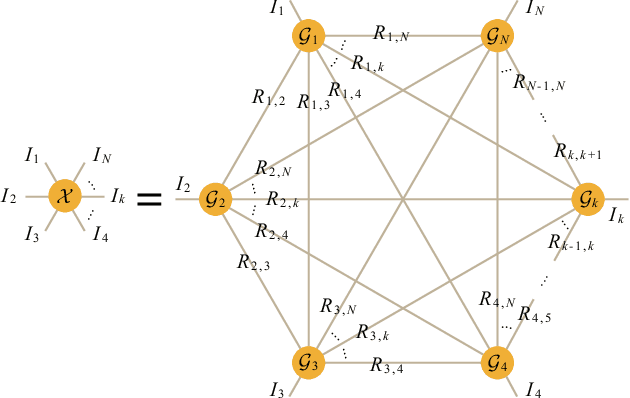
Remote sensing image (RSI) inpainting plays an important role in real applications. Recently, fully-connected tensor network (FCTN) decomposition has been shown the remarkable ability to fully characterize the global correlation. Considering the global correlation and the nonlocal self-similarity (NSS) of RSIs, this paper introduces the FCTN decomposition to the whole RSI and its NSS groups, and proposes a novel nonlocal patch-based FCTN (NL-FCTN) decomposition for RSI inpainting. Different from other nonlocal patch-based methods, the NL-FCTN decomposition-based method, which increases tensor order by stacking similar small-sized patches to NSS groups, cleverly leverages the remarkable ability of FCTN decomposition to deal with higher-order tensors. Besides, we propose an efficient proximal alternating minimization-based algorithm to solve the proposed NL-FCTN decomposition-based model with a theoretical convergence guarantee. Extensive experiments on RSIs demonstrate that the proposed method achieves the state-of-the-art inpainting performance in all compared methods.

Hyperspectral Denoising Using Unsupervised Disentangled Spatio-Spectral Deep Priors

Image denoising is often empowered by accurate prior information. In recent years, data-driven neural network priors have shown promising performance for RGB natural image denoising. Compared to classic handcrafted priors (e.g., sparsity and total variation), the "deep priors" are learned using a large number of training samples -- which can accurately model the complex image generating process. However, data-driven priors are hard to acquire for hyperspectral images (HSIs) due to the lack of training data. A remedy is to use the so-called unsupervised deep image prior (DIP). Under the unsupervised DIP framework, it is hypothesized and empirically demonstrated that proper neural network structures are reasonable priors of certain types of images, and the network weights can be learned without training data. Nonetheless, the most effective unsupervised DIP structures were proposed for natural images instead of HSIs. The performance of unsupervised DIP-based HSI denoising is limited by a couple of serious challenges, namely, network structure design and network complexity. This work puts forth an unsupervised DIP framework that is based on the classic spatio-spectral decomposition of HSIs. Utilizing the so-called linear mixture model of HSIs, two types of unsupervised DIPs, i.e., U-Net-like network and fully-connected networks, are employed to model the abundance maps and endmembers contained in the HSIs, respectively. This way, empirically validated unsupervised DIP structures for natural images can be easily incorporated for HSI denoising. Besides, the decomposition also substantially reduces network complexity. An efficient alternating optimization algorithm is proposed to handle the formulated denoising problem. Semi-real and real data experiments are employed to showcase the effectiveness of the proposed approach.

Unsupervised Hyperspectral Mixed Noise Removal Via Spatial-Spectral Constrained Deep Image Prior

Hyperspectral images (HSIs) are unavoidably corrupted by mixed noise which hinders the subsequent applications. Traditional methods exploit the structure of the HSI via optimization-based models for denoising, while their capacity is inferior to the convolutional neural network (CNN)-based methods, which supervisedly learn the noisy-to-denoised mapping from a large amount of data. However, as the clean-noisy pairs of hyperspectral data are always unavailable in many applications, it is eager to build an unsupervised HSI denoising method with high model capability. To remove the mixed noise in HSIs, we suggest the spatial-spectral constrained deep image prior (S2DIP), which simultaneously capitalize the high model representation ability brought by the CNN in an unsupervised manner and does not need any extra training data. Specifically, we employ the separable 3D convolution blocks to faithfully encode the HSI in the framework of DIP, and a spatial-spectral total variation (SSTV) term is tailored to explore the spatial-spectral smoothness of HSIs. Moreover, our method favorably addresses the semi-convergence behavior of prevailing unsupervised methods, e.g., DIP 2D, and DIP 3D. Extensive experiments demonstrate that the proposed method outperforms state-of-the-art optimization-based HSI denoising methods in terms of effectiveness and robustness.

Tensor N-tubal rank and its convex relaxation for low-rank tensor recovery

As low-rank modeling has achieved great success in tensor recovery, many research efforts devote to defining the tensor rank. Among them, the recent popular tensor tubal rank, defined based on the tensor singular value decomposition (t-SVD), obtains promising results. However, the framework of the t-SVD and the tensor tubal rank are applicable only to three-way tensors and lack of flexibility to handle different correlations along different modes. To tackle these two issues, we define a new tensor unfolding operator, named mode-$k_1k_2$ tensor unfolding, as the process of lexicographically stacking the mode-$k_1k_2$ slices of an $N$-way tensor into a three-way tensor, which is a three-way extension of the well-known mode-$k$ tensor matricization. Based on it, we define a novel tensor rank, the tensor $N$-tubal rank, as a vector whose elements contain the tubal rank of all mode-$k_1k_2$ unfolding tensors, to depict the correlations along different modes. To efficiently minimize the proposed $N$-tubal rank, we establish its convex relaxation: the weighted sum of tensor nuclear norm (WSTNN). Then, we apply WSTNN to low-rank tensor completion (LRTC) and tensor robust principal component analysis (TRPCA). The corresponding WSTNN-based LRTC and TRPCA models are proposed, and two efficient alternating direction method of multipliers (ADMM)-based algorithms are developed to solve the proposed models. Numerical experiments demonstrate that the proposed models significantly outperform the compared ones.