Nonlocal Patch-Based Fully-Connected Tensor Network Decomposition for Remote Sensing Image Inpainting

Remote sensing image (RSI) inpainting plays an important role in real applications. Recently, fully-connected tensor network (FCTN) decomposition has been shown the remarkable ability to fully characterize the global correlation. Considering the global correlation and the nonlocal self-similarity (NSS) of RSIs, this paper introduces the FCTN decomposition to the whole RSI and its NSS groups, and proposes a novel nonlocal patch-based FCTN (NL-FCTN) decomposition for RSI inpainting. Different from other nonlocal patch-based methods, the NL-FCTN decomposition-based method, which increases tensor order by stacking similar small-sized patches to NSS groups, cleverly leverages the remarkable ability of FCTN decomposition to deal with higher-order tensors. Besides, we propose an efficient proximal alternating minimization-based algorithm to solve the proposed NL-FCTN decomposition-based model with a theoretical convergence guarantee. Extensive experiments on RSIs demonstrate that the proposed method achieves the state-of-the-art inpainting performance in all compared methods.

Image segmentation based on the hybrid total variation model and the K-means clustering strategy

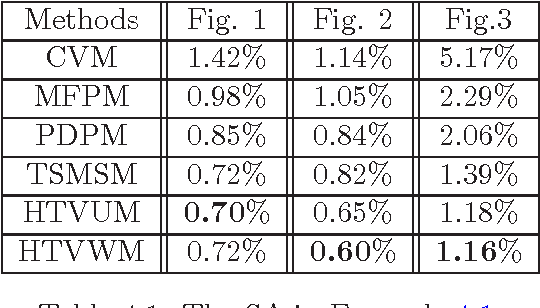
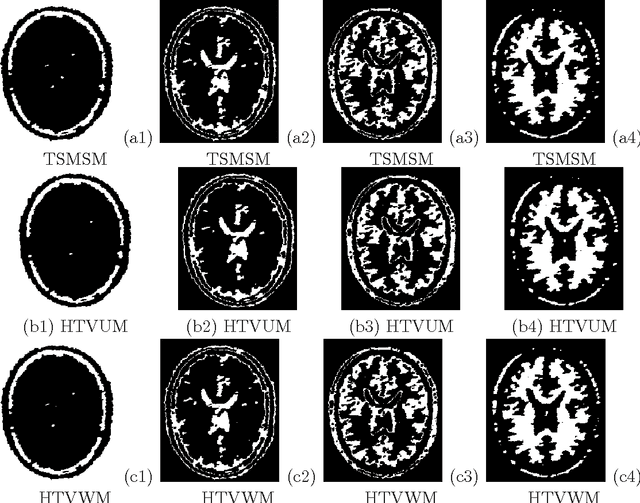
The performance of image segmentation highly relies on the original inputting image. When the image is contaminated by some noises or blurs, we can not obtain the efficient segmentation result by using direct segmentation methods. In order to efficiently segment the contaminated image, this paper proposes a two step method based on the hybrid total variation model with a box constraint and the K-means clustering method. In the first step, the hybrid model is based on the weighted convex combination between the total variation functional and the high-order total variation as the regularization term to obtain the original clustering data. In order to deal with non-smooth regularization term, we solve this model by employing the alternating split Bregman method. Then, in the second step, the segmentation can be obtained by thresholding this clustering data into different phases, where the thresholds can be given by using the K-means clustering method. Numerical comparisons show that our proposed model can provide more efficient segmentation results dealing with the noise image and blurring image.

The proximal point method for a hybrid model in image restoration

Models including two $L^1$ -norm terms have been widely used in image restoration. In this paper we first propose the alternating direction method of multipliers (ADMM) to solve this class of models. Based on ADMM, we then propose the proximal point method (PPM), which is more efficient than ADMM. Following the operator theory, we also give the convergence analysis of the proposed methods. Furthermore, we use the proposed methods to solve a class of hybrid models combining the ROF model with the LLT model. Some numerical results demonstrate the viability and efficiency of the proposed methods.